Regression Based Latent Factor Models Deepak Agarwal BeeChung

Regression Based Latent Factor Models Deepak Agarwal Bee-Chung Chen Yahoo! Research KDD 2009, Paris 6/29/2009

OUTLINE • Problem Definition – Predicting dyadic response exploiting covariate information • Factorization models – Brief Overview • Incorporating covariate information through regressions – Cold start and warm-start through a single model • Closer look at induced correlations • Fitting algorithms : Monte Carlo EM and Iterated CM • Experiments – Movie Lens – Yahoo! Front Page • Summary -2 -

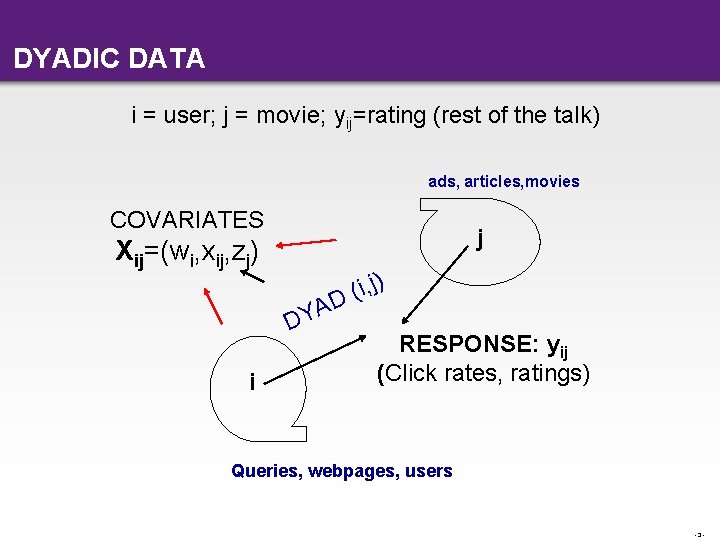
DYADIC DATA i = user; j = movie; yij=rating (rest of the talk) ads, articles, movies COVARIATES j Xij=(wi, xij, zj) A DY i i, j) ( D RESPONSE: yij (Click rates, ratings) Queries, webpages, users -3 -

PROBLEM DEFINITION • Models to predict ratings for new dyads – Warm-start: (user, movie) present in the training data – Cold-start: At least one of (user, movie) new • Challenges – Highly incomplete (user, movie) matrix – Heavy tailed degree distributions for users/movies • Large fraction of ratings from small fraction of users/movies – Handling both warm-start and cold-start effectively -4 -

Possible approaches • Large scale regression based on covariates – Does not provide good estimates for heavy users/movies – Large number of predictors to estimate interactions • Collaborative filtering – Neighborhood based – Factorization (our approach in this paper) – Good for warm-start; cold-start dealt with separately • Single model that handles cold-start and warm-start – Heavy users/movies → User/movie specific model – Light users/movies → fallback on regression model – Smooth fallback mechanism for good performance -5 -

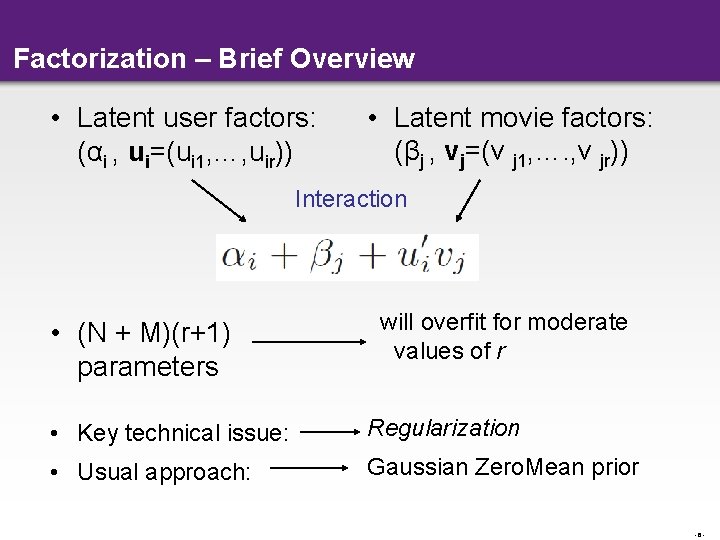
Factorization – Brief Overview • Latent user factors: (αi , ui=(ui 1, …, uir)) • Latent movie factors: (βj , vj=(v j 1, …. , v jr)) Interaction • (N + M)(r+1) parameters will overfit for moderate values of r • Key technical issue: Regularization • Usual approach: Gaussian Zero. Mean prior -6 -

Existing Zero-Mean Factorization Model Observation Equation State Equation Predict for new dyad: -7 -

Regression-based Factorization Model (RLFM) • Main idea: Flexible prior, predict factors through regressions • Seamlessly handles cold-start and warm-start • Modified state equation to incorporate covariates -8 -

Advantages of RLFM • Better regularization of factors – Covariates “shrink” towards a better centroid • Cold-start: Fallback regression model (Feature. Only) -9 -

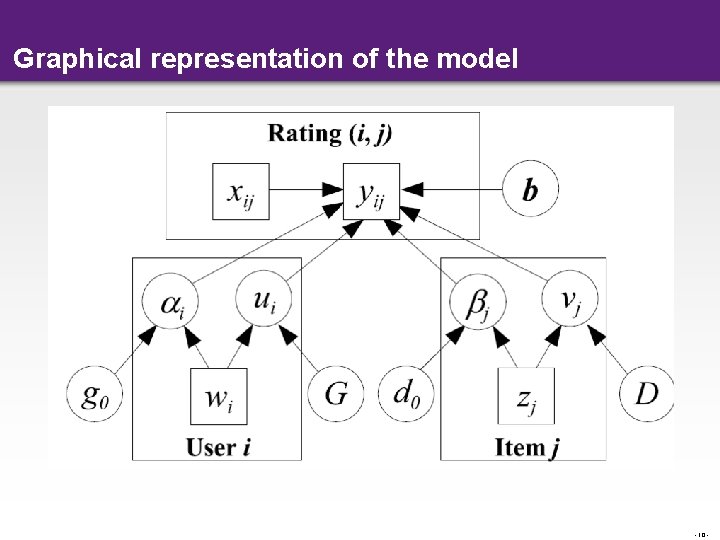
Graphical representation of the model - 10 -

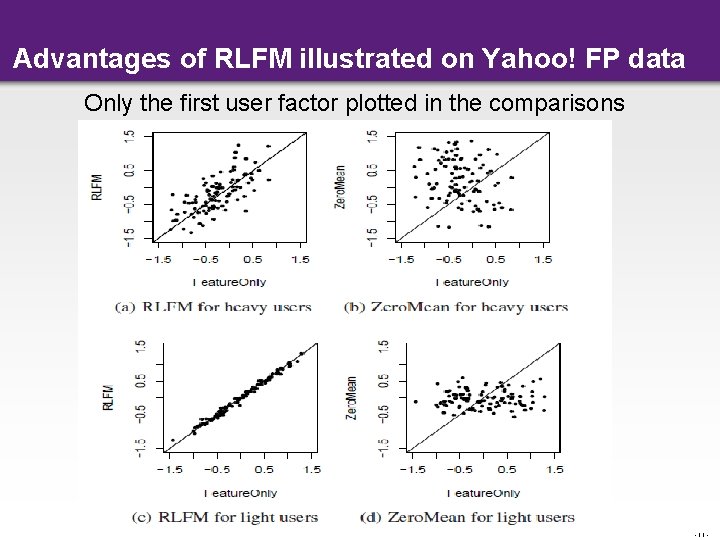
Advantages of RLFM illustrated on Yahoo! FP data Only the first user factor plotted in the comparisons - 11 -

Induced correlations among observations Hierarchical random-effects model Marginal distribution obtained by integrating out random effects - 12 -

Closer look at induced marginal correlations - 13 -

Model Fitting • Challenging, multi-modal posterior • Monte-Carlo EM (MCEM) – E-step: Sample factors through Gibbs sampling – M-step: Estimate regressions through off-the-shelf linear regression routines using sampled factors as response • We used t-regression, others like LASSO could be used • Iterated Conditional Mode (ICM) – Replace E-step by CG : conditional modes of factors – M-step: Estimate regressions using the modes as response • Incorporating uncertainty in factor estimates in MCEM helps - 14 -

Monte Carlo E-step • Through a vanilla Gibbs sampler (conditionals closed form) • Other conditionals also Gaussian and closed form • Conditionals of users (movies) sampled simultaneously • Small number of samples in early iterations, large numbers in later iterations - 15 -

M-step (Why MCEM is better than ICM) • Update G, optimize • Update Au=au I Ignored by ICM, underestimates factor variability Factors over-shrunk, posterior not explored well - 16 -

Experiment 1: Better regularization • Movie. Lens-100 K, avg RMSE using pre-specified splits • Zero. Mean, RLFM and Feature. Only (no cold-start issues) • Covariates: – Users : age, gender, zipcode (1 st digit only) – Movies: genres - 17 -

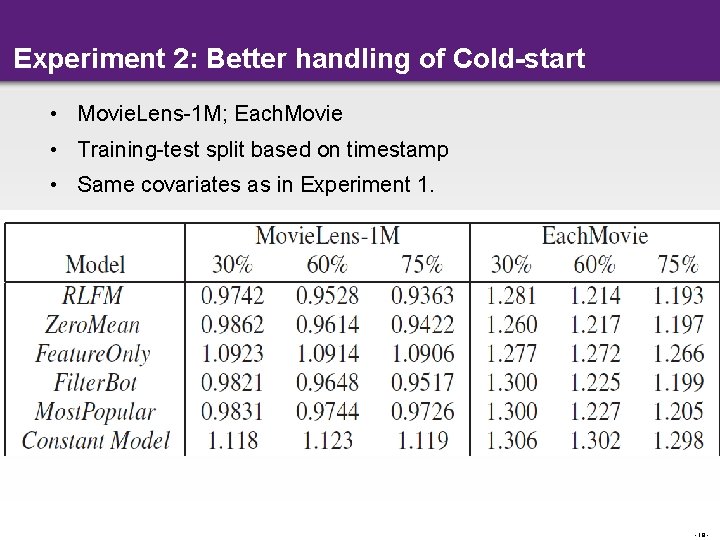
Experiment 2: Better handling of Cold-start • Movie. Lens-1 M; Each. Movie • Training-test split based on timestamp • Same covariates as in Experiment 1. - 18 -

Experiment 3: Online updates help • Covariates provide good initialization for new user/movie factors but updating factor estimates frequently (e. g. every hour) helps • Dyn-RLFM – Estimate posterior mean and covariance at the end of MCEM by running large number of Gibbs iterations – For online updates, we do not change the posterior covariance but only adapt the posterior means through EWMA • This is done by running small number of Gibbs iterations - 19 -

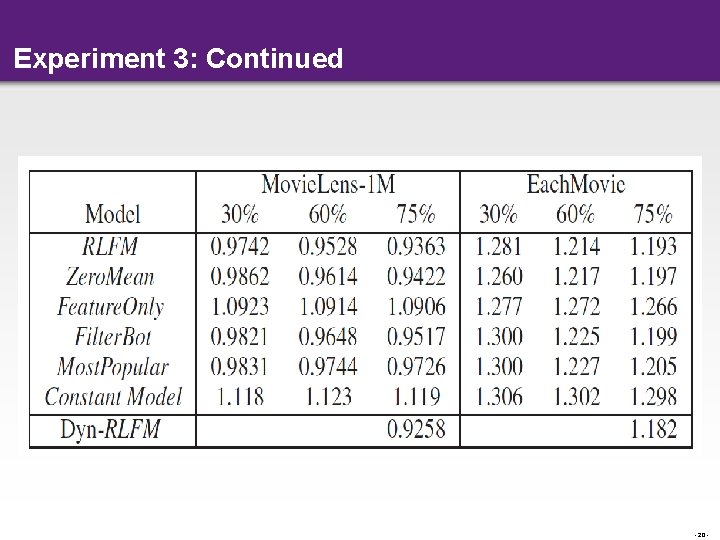
Experiment 3: Continued - 20 -

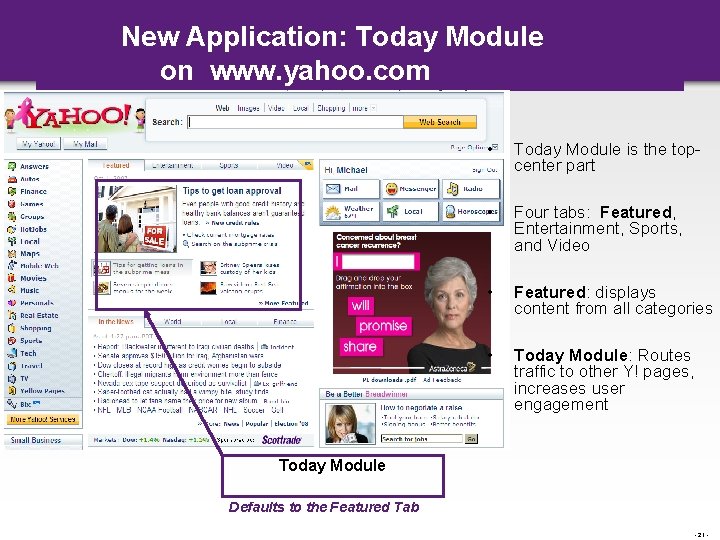
New Application: Today Module on www. yahoo. com • Today Module is the topcenter part • Four tabs: Featured, Entertainment, Sports, and Video • Featured: displays content from all categories • Today Module: Routes traffic to other Y! pages, increases user engagement Today Module Defaults to the Featured Tab - 21 -

Some More Background… Featured Tab in Detail • Four articles on F 1, F 2, F 3, F 4 • F 1 article as story by default STORY POSITION F 1 F 3 F 2 F 4 FOOTER POSITION • Footer click → corresponding article as story • Click rates (CTR): Story clicks per display (maximize this) • F 1 → max exposure, large fraction of story clicks - 22 -

Experiment 4: Predicting click-rate on articles • Goal: Predict click-rate on articles for a user on F 1 position • Article lifetimes short, dynamic updates important • User covariates: – Age, Gender, Geo, Browse behavior • Article covariates – Content Category, keywords • 2 M ratings, 30 K users, 4. 5 K articles - 23 -

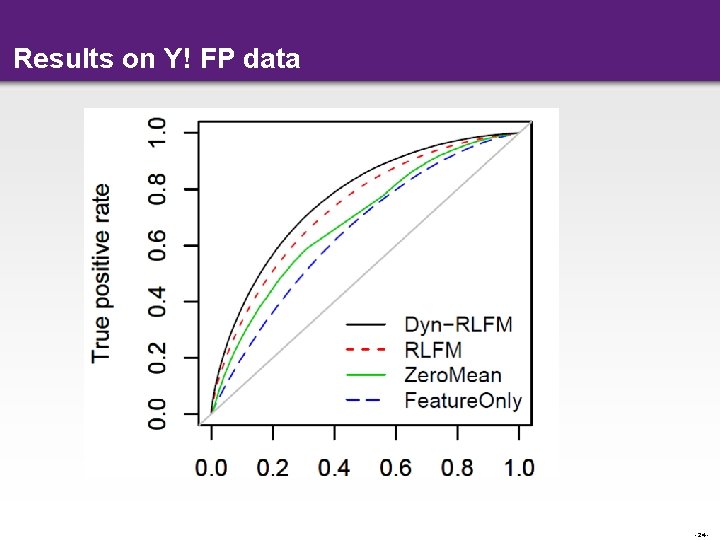
Results on Y! FP data - 24 -

Related Work • Little work in a model based framework in the past – PDLF, KDD 07 (does not predict factors using covariates) • Recent work at WWW 09 published in parallel – Matchbox: Bayesian online recommendation algorithm • Both models same (motivation different), • Estimation methods different – Matchbox based on variational Bayes, we conjecture the performance would be similar to the ICM method • Some papers at ICML this year are also related – (not done with my reading yet) - 25 -

Summary • Regularizing factors through covariates effective • We presented a regression based factor model that regularizes better and deals with both cold-start and warmstart in a single framework in a seamless way • Fitting method scalable; Gibbs sampling for users and movies can be done in parallel. Regressions in M-step can be done with any off-the-shelf scalable linear regression routine • Good results on benchmark data and a new Y! FP data - 26 -

Ongoing Work • Investigating various non-linear regressions in M-step • Better MCMC sampling schemes for faster convergence • Addressing model choice issues (through Bayes factors) • Tensor factorization - 27 -