Regression Analysis Modeling Relationships 1 Regression Analysis is

Regression Analysis Modeling Relationships 1

Regression Analysis is a study of the relationship between a set of independent variables and the dependent variable. The Linear Equation representing the ‘true’ or population relationship: Dependent Variable Independent Variables 2

Variables Dependent Variable: Also called the predicted variable. Its value depends on, or can be predicted by the independent variables. Independent Variables: Also called the predictor variables. These can be measured directly, and are used to predict the dependent (or to simply understand it better). 3

Modeling Process Define Goal To study the impact of various factors on individual health Choose y Lung Capacity, measured in cc. List possible Xs Minutes of Exercise per day, # of days/week of exercise, ethnicity, gender, age, height, altitude at which lived. Collect Data Primary, Secondary sources Preliminary Analyses Univariate, bivariate Build Regression Model How is y related to all the Xs? Evaluate Model How good is the model at predicting y? Implement/Monitor Create DSS, monitor, update 4

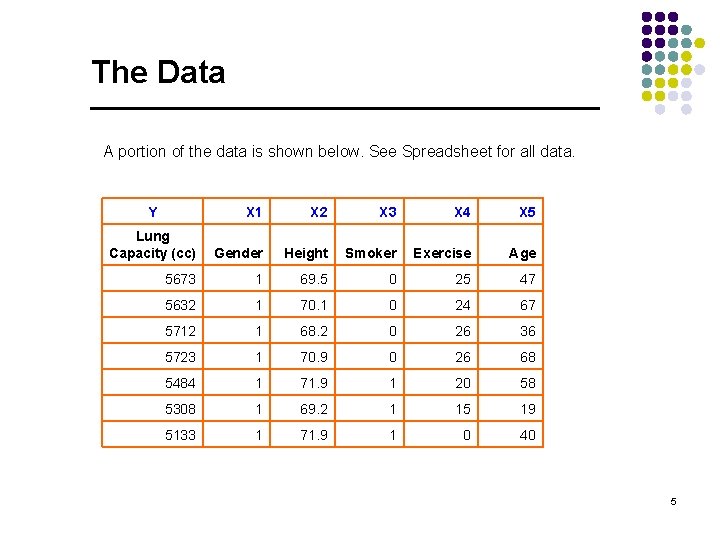
The Data A portion of the data is shown below. See Spreadsheet for all data. Y X 1 X 2 X 3 X 4 X 5 Lung Capacity (cc) Gender Height Smoker Exercise Age 5673 1 69. 5 0 25 47 5632 1 70. 1 0 24 67 5712 1 68. 2 0 26 36 5723 1 70. 9 0 26 68 5484 1 71. 9 1 20 58 5308 1 69. 2 1 15 19 5133 1 71. 9 1 0 40 5

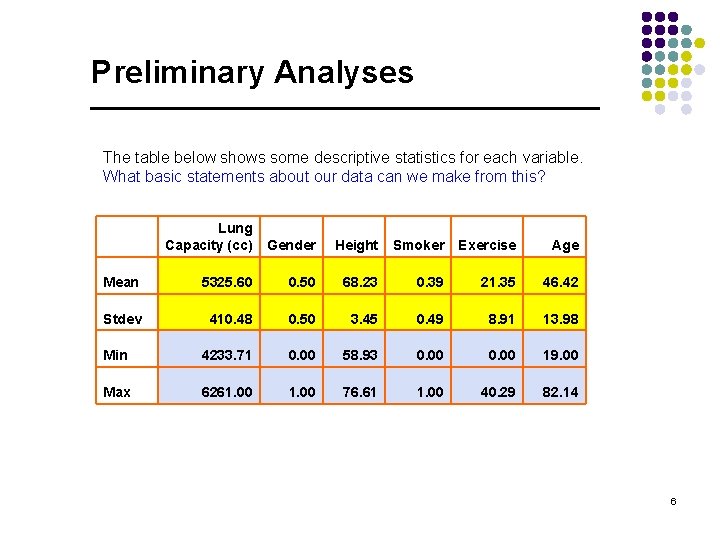
Preliminary Analyses The table below shows some descriptive statistics for each variable. What basic statements about our data can we make from this? Lung Capacity (cc) Gender Height Smoker Exercise Age Mean 5325. 60 0. 50 68. 23 0. 39 21. 35 46. 42 Stdev 410. 48 0. 50 3. 45 0. 49 8. 91 13. 98 Min 4233. 71 0. 00 58. 93 0. 00 19. 00 Max 6261. 00 76. 61 1. 00 40. 29 82. 14 6

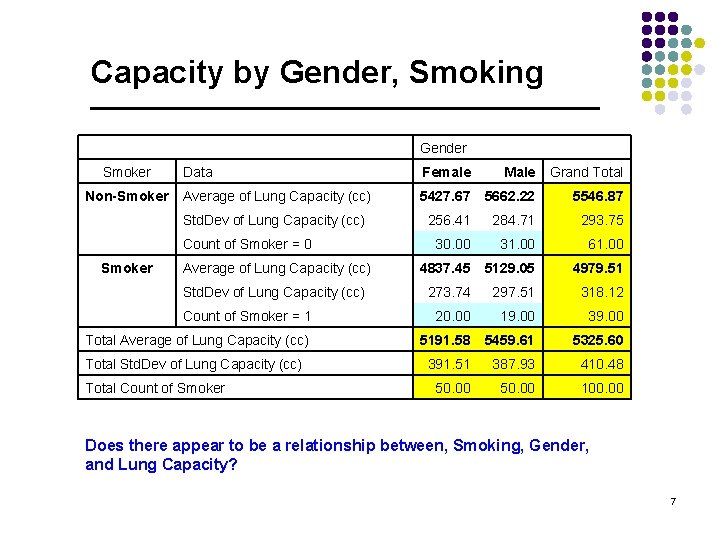
Capacity by Gender, Smoking Gender Data Female Male Grand Total Non-Smoker Average of Lung Capacity (cc) 5427. 67 5662. 22 5546. 87 Std. Dev of Lung Capacity (cc) 256. 41 284. 71 293. 75 Count of Smoker = 0 30. 00 31. 00 61. 00 Smoker Average of Lung Capacity (cc) 4837. 45 5129. 05 4979. 51 Std. Dev of Lung Capacity (cc) 273. 74 297. 51 318. 12 Count of Smoker = 1 20. 00 19. 00 39. 00 Total Average of Lung Capacity (cc) 5191. 58 5459. 61 5325. 60 Total Std. Dev of Lung Capacity (cc) 391. 51 387. 93 410. 48 50. 00 100. 00 Total Count of Smoker Does there appear to be a relationship between, Smoking, Gender, and Lung Capacity? 7

Distributions 8

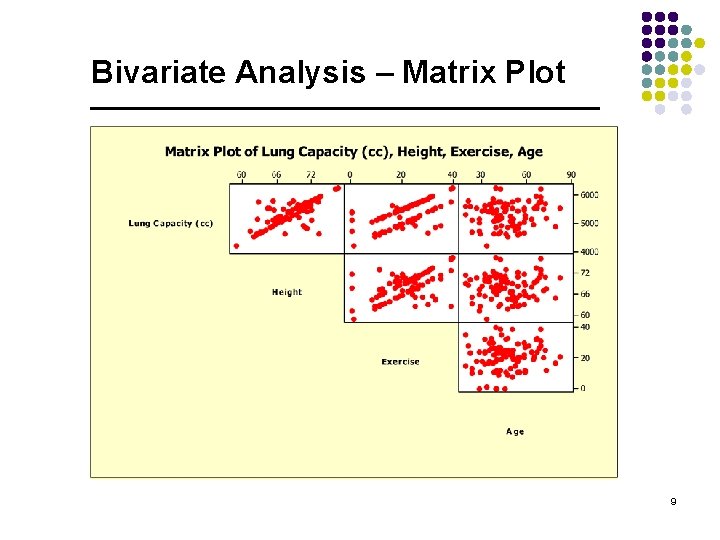
Bivariate Analysis – Matrix Plot 9

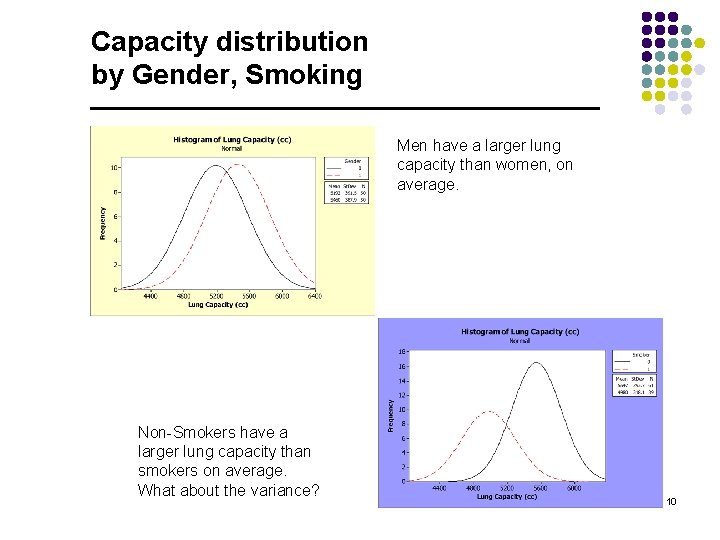
Capacity distribution by Gender, Smoking Men have a larger lung capacity than women, on average. Non-Smokers have a larger lung capacity than smokers on average. What about the variance? 10

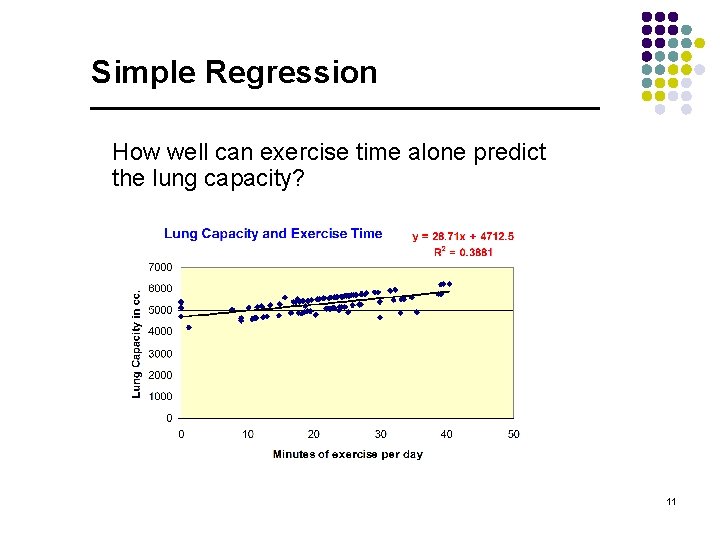
Simple Regression How well can exercise time alone predict the lung capacity? 11

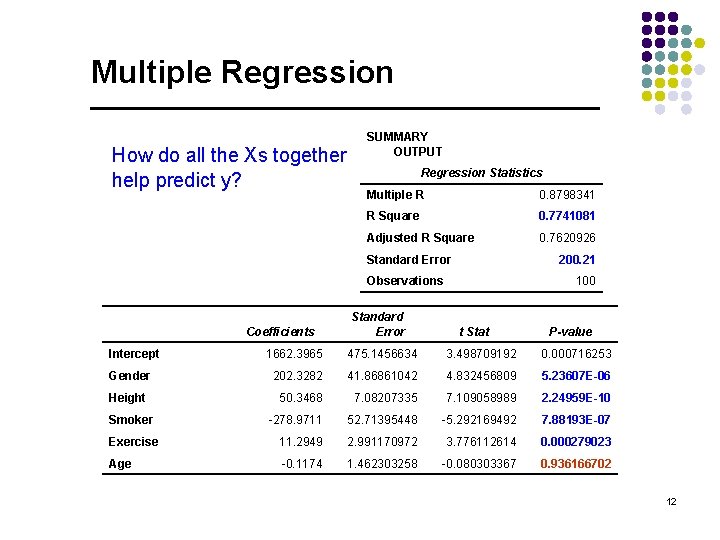
Multiple Regression How do all the Xs together help predict y? SUMMARY OUTPUT Regression Statistics Multiple R 0. 8798341 R Square 0. 7741081 Adjusted R Square 0. 7620926 Standard Error 200. 21 Observations Intercept Coefficients Standard Error 100 t Stat P-value 1662. 3965 475. 1456634 3. 498709192 0. 000716253 Gender 202. 3282 41. 86861042 4. 832456809 5. 23607 E-06 Height 50. 3468 7. 08207335 7. 109058989 2. 24959 E-10 -278. 9711 52. 71395448 -5. 292169492 7. 88193 E-07 Exercise 11. 2949 2. 991170972 3. 776112614 0. 000279023 Age -0. 1174 1. 462303258 -0. 080303367 0. 936166702 Smoker 12

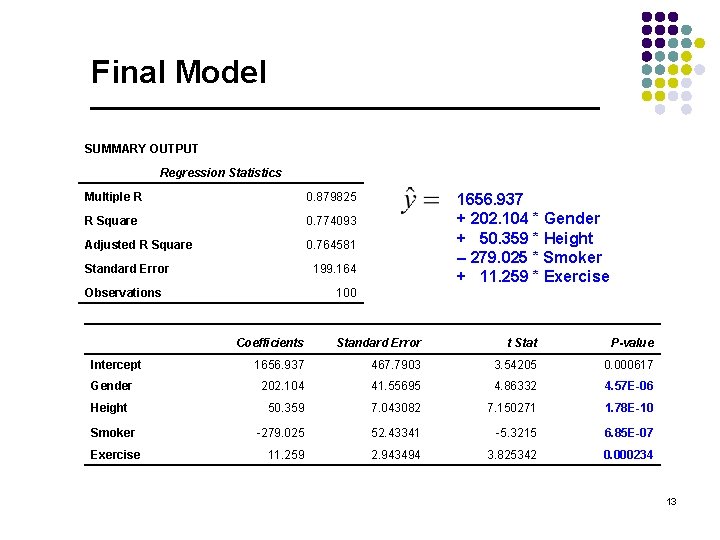
Final Model SUMMARY OUTPUT Regression Statistics Multiple R 0. 879825 R Square 0. 774093 Adjusted R Square 0. 764581 Standard Error 1656. 937 + 202. 104 * Gender + 50. 359 * Height – 279. 025 * Smoker + 11. 259 * Exercise 199. 164 Observations 100 Coefficients Standard Error t Stat P-value Intercept 1656. 937 467. 7903 3. 54205 0. 000617 Gender 202. 104 41. 55695 4. 86332 4. 57 E-06 Height 50. 359 7. 043082 7. 150271 1. 78 E-10 -279. 025 52. 43341 -5. 3215 6. 85 E-07 11. 259 2. 943494 3. 825342 0. 000234 Smoker Exercise 13

Prediction Exercise 1. Predict the lung capacity for a nonsmoking female who does not exercise, and is 66 inches tall, based on the model above. 2. What would be the predicted value if she smoked? 3. What would it be for a male in both the above cases? 14