REGRESION LINEAL SIMPLE Una de las aplicaciones mas

REGRESION LINEAL SIMPLE

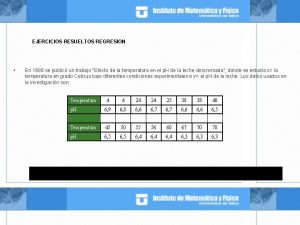
Una de las aplicaciones mas importantes de la estadística implica la estimación del valor medio de una variable de respuesta y o la predicción de algún valor futuro de y con base el conocimiento de un conjunto de variables independientes relacionadas, x 1, x 2, . . . xk.

Los modelos que se emplean para relacionar una variable dependiente y con las variables independientes x 1, x 2, . . . xk se denominan modelos de regresión o modelos estadísticos lineales porque expresan el valor medio de y para valores dados de x 1, x 2, . . . xk como una función lineal de un conjunto de parámetros desconocidos.

Los conceptos de análisis de regresión se presentan empleando un modelo de regresión muy sencillo, uno que relaciona y con una sola variable x. Aprenderemos a ajustar este modelo a un conjunto de datos mediante el método de los mínimos cuadrados.

Examinaremos los diferentes tipos de inferencias que pueden hacerse a partir de un análisis de regresión.

Un modelo de regresión simple: supuestos Supongamos que se quiere determinar la magnitud de la compresión que se producirá en un tipo de material de 2 pulgadas de espesor cuando se someta a diferentes cantidades de presión.

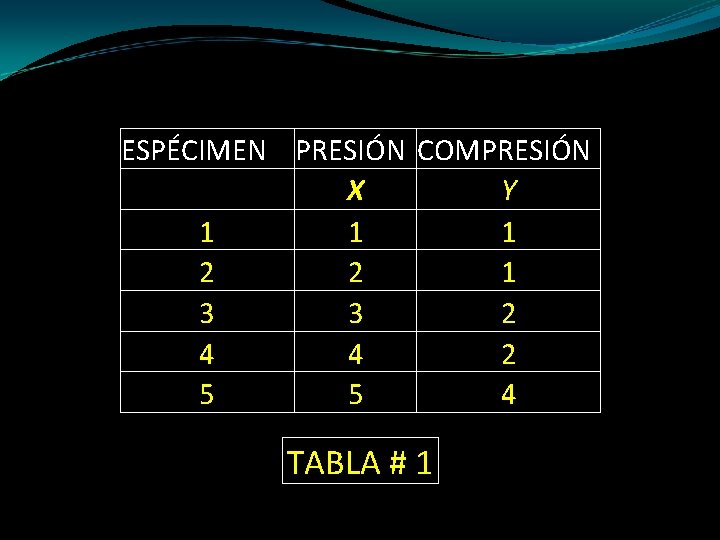
Un modelo de regresión simple: supuestos Se prueban cinco trozos experimentales del material bajo diferentes presiones. Los valores de x (en unidades de 10 libras por pulgada cuadrada) y las magnitudes de compresión y resultantes (en unidades de 0. 1 de pulgada) se presentan en la tabla 1.

ESPÉCIMEN PRESIÓN COMPRESIÓN X Y 1 1 1 2 2 1 3 3 2 4 4 2 5 5 4 TABLA # 1

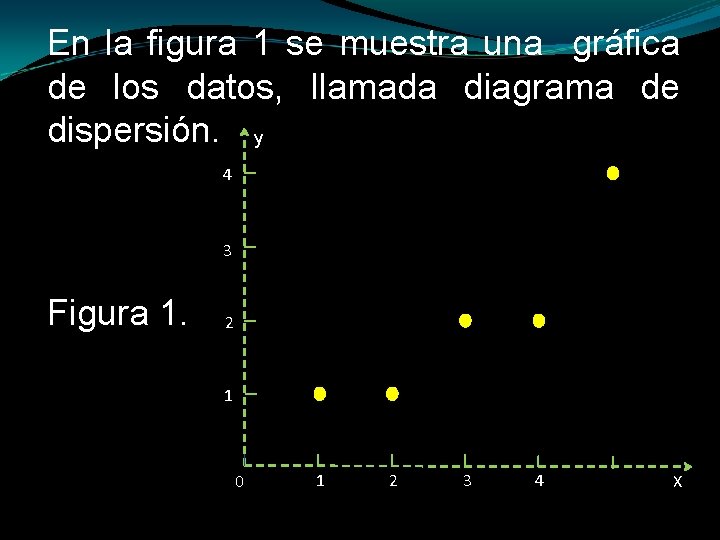
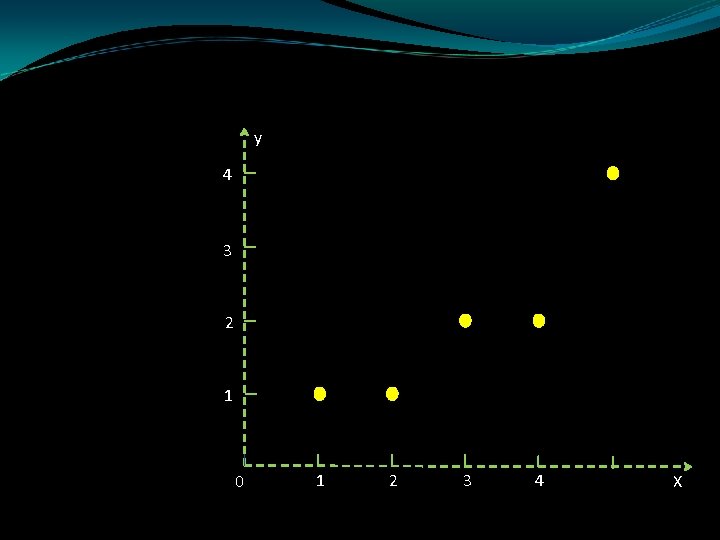
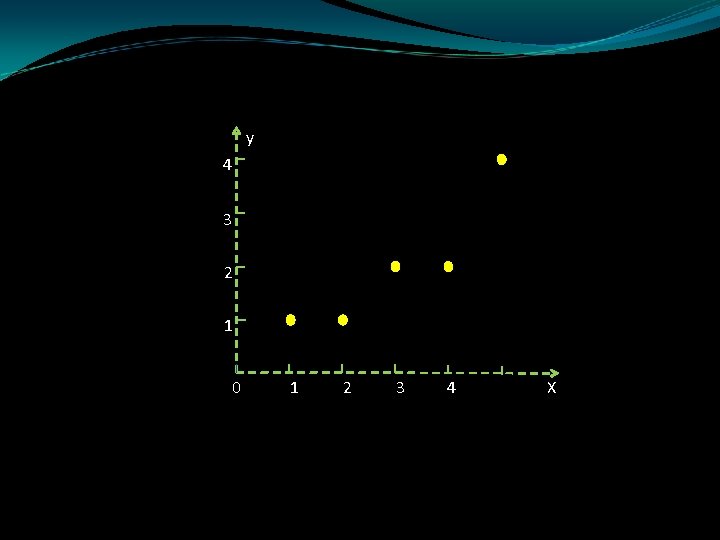
En la figura 1 se muestra una gráfica de los datos, llamada diagrama de dispersión. y 4 3 Figura 1. 2 1 0 1 2 3 4 X

y 4 3 2 1 0 1 2 3 4 X

y 4 3 2 1 0 1 2 3 4 X

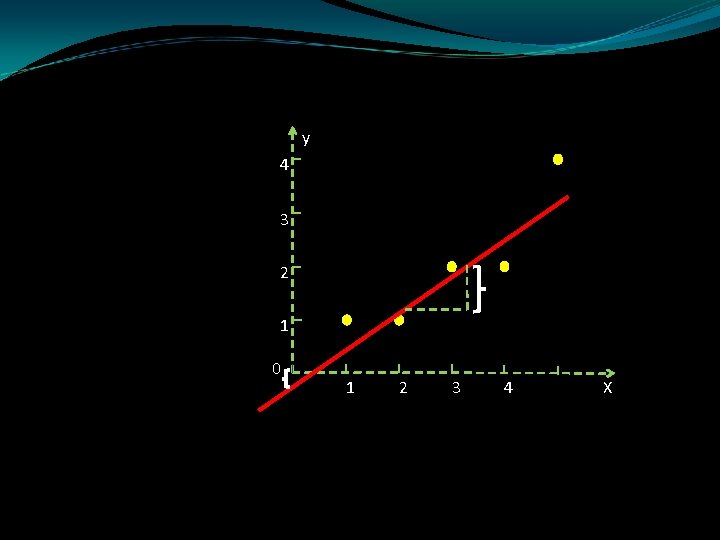
y 4 3 2 1 0 1 2 3 4 5 Supongamos que creemos que el valor de y tiende a aumentar de forma conforme x X lineal aumenta Entonces, podríamos escoger un modelo que relacione a y con x trazando una línea recta a través de los puntos de la figura.

y 4 3 2 1 0 1 2 3 4 5 X Semejante modelo determinístico (uno que no contempla errores de predicción) podría ser adecuado si todos los puntos de la figura quedaran sobre la línea ajustada.

La solución es construir un modelo probabilístico que relacione y con x; uno que contemple la variación aleatoria de los puntos de datos a los lados de una línea recta.

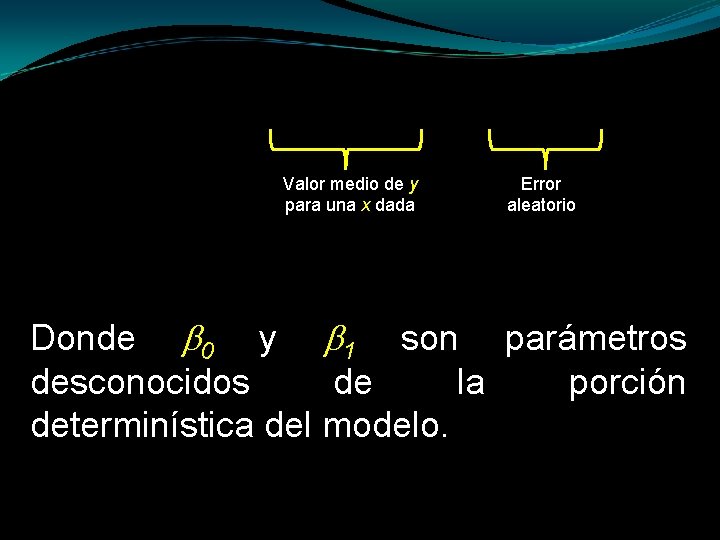
Un tipo de modelo probabilístico, el modelo de regresión lineal simple, supone que el valor medio de y para un valor dado de x se grafica como una línea recta y que los puntos se desvían de esta línea de medias en una cantidad aleatoria (positiva o negativa) igual a , es decir:

Valor medio de y para una x dada Error aleatorio Donde 0 y 1 son parámetros desconocidos de la porción determinística del modelo.

Valor medio de y para una x dada Error aleatorio Si suponemos que los puntos se desvían por encima y por debajo de la líneas de medias, siendo algunas desviaciones positivas, otras negativas, y con E( ) = 0, entonces el valor medio de y es:

Por lo tanto, el valor medio de y para un valor dado de x, representado por el símbolo E(y), se grafica como una línea recta con ordenada al origen igual a 0 y pendiente igual a 1

y 4 3 2 1 0 1 2 3 4 X

Modelo de regresión lineal simple (probabilístico) Donde: y = variable dependiente x = variable independiente E(y)= 0+ 1 x es el componente determinístico (la ecuación de una línea recta) = componente de error aleatorio 0 = punto en que la línea corta el eje y 1 = pendiente de la línea

Si queremos ajustar un modelo de regresión lineal simple a un conjunto de datos, debemos encontrar estimadores para los parámetros desconocidos, 0 y 1.

Los supuestos, que se resumirán a continuación, son básicos para todo análisis de regresión estadístico.

SUPUESTO 1: La media de la distribución de probabilidad de es cero. Es decir, la media de los errores a lo largo de una serie infinitamente larga de experimentos es cero para cada valor de la variable independiente x. Este supuesto implica que el valor medio de y, E(y), para un valor dado de x es E(y)= 0+ 1 x

SUPUESTO 2: La varianza de la distribución de probabilidad de es constante para todos los valores de la variable independiente x SUPUESTO 3: La distribución de probabilidad de es normal

SUPUESTO 4: Los errores asociados a cualquier dos observaciones distintas son independientes. Es decir, el error asociado a un valor de y en particular no tiene efecto alguno sobre los errores asociados a otros valores de y

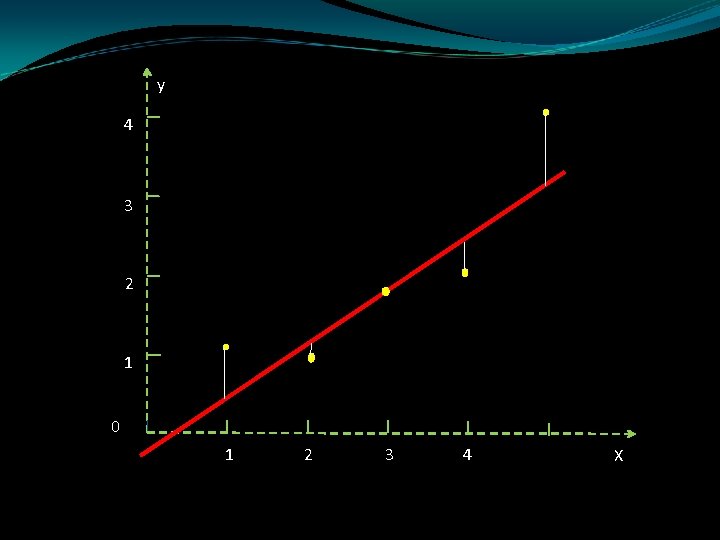
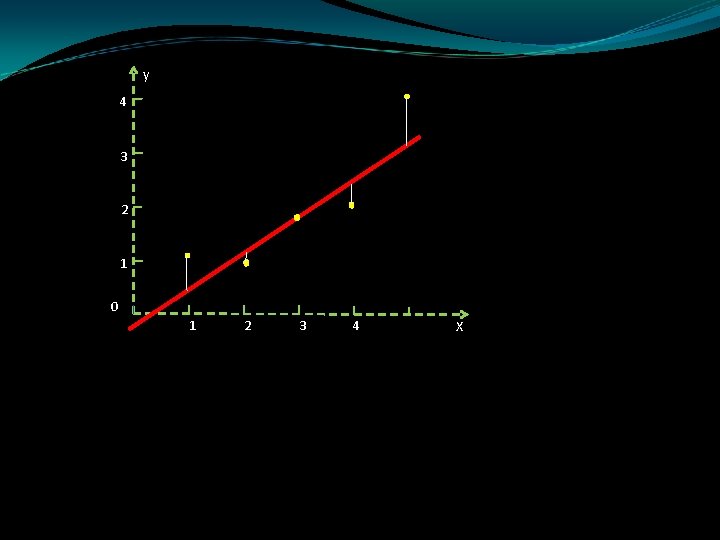
ESTIMACIÓN DE 0 y 1: EL METODO DE LOS MÍNIMOS CUADRADOS La suma de los cuadrados de las desviaciones se denomina suma de los cuadrados del error y se denota con el símbolo SSE. La línea recibe el nombre de línea de mínimos cuadrados, línea de regresión o ecuación de mínimos cuadrados.

y 4 3 2 1 0 1 2 3 4 X

y 4 3 2 1 0 1 2 3 4 X

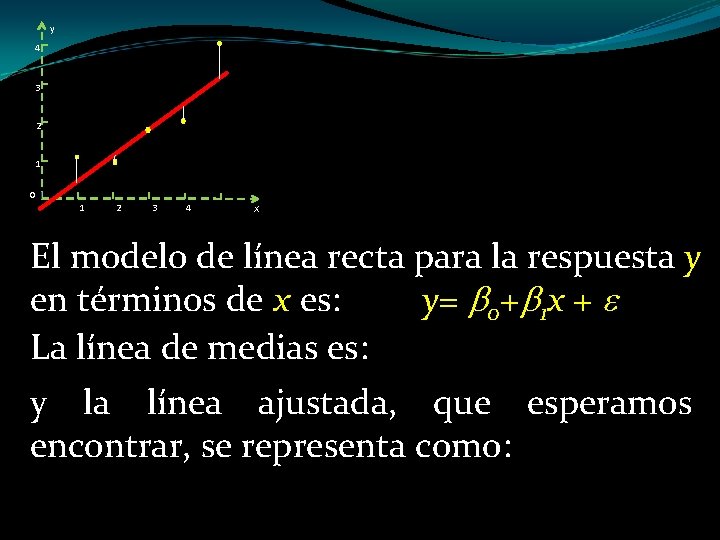
y 4 3 2 1 0 1 2 3 4 X El modelo de línea recta para la respuesta y en términos de x es: y= 0+ 1 x + La línea de medias es: E(y)= 0+ 1 x y la línea ajustada, que esperamos encontrar, se representa como:

Formulas para las estimaciones de mínimos cuadrados Pendiente: Ordenada al origen: Donde:

Ejercicio: A continuación tenemos las estaturas en centímetros (muestra x) y el peso en kilogramos (y) de niños de 6 años. Niño 1 2 3 4 5 6 7 8 9 10 Estatura 121 123 108 111 109 114 103 110 115 (cm) x Peso 25 22 19 24 19 18 20 15 20 21 (kg) y

Ejercicio: Calcular: las medidas centrales, el primero y segundo cuartil, los percentiles 30 y 70, el diagrama de dispersión

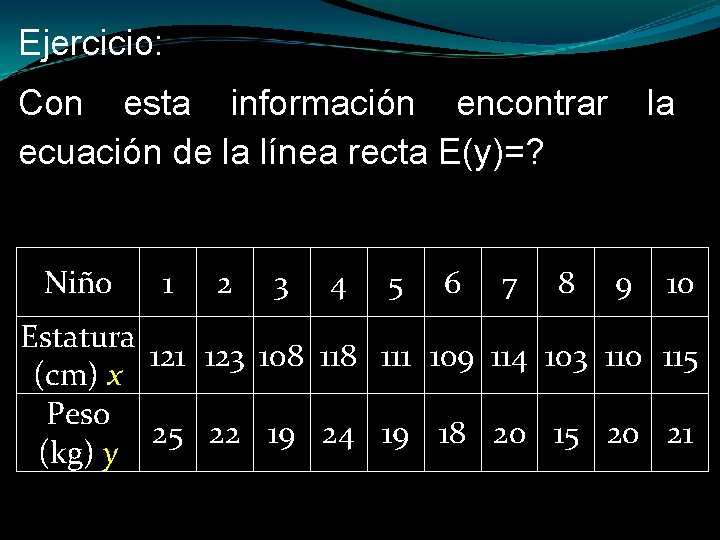
Ejercicio: Con esta información encontrar ecuación de la línea recta E(y)=? Niño 1 2 3 4 5 6 7 8 la 9 10 Estatura 121 123 108 111 109 114 103 110 115 (cm) x Peso 25 22 19 24 19 18 20 15 20 21 (kg) y