Regresijos modelio matematin iraika 2017 03 28 1

Regresijos modelio matematinė išraiška 2017 -03 -28 1. Gujarati D. N. Basic Econometrics. 6 chapter. Extension of the Two Variable Linear regression Model. Mc. Graw-Hill Inc, 1995. 2005 ir kt leidimai

Paskaitos dalys Porinės regresijos kintamųjų priklausomybės matematinė išraiška ¡ Dauginės regresijos kintamųjų matematinė išraiška ¡ Regresinio modelio skaičiavimo rezultatų pateikimas ¡

Porinio regresinio modelio matematinė išraiška

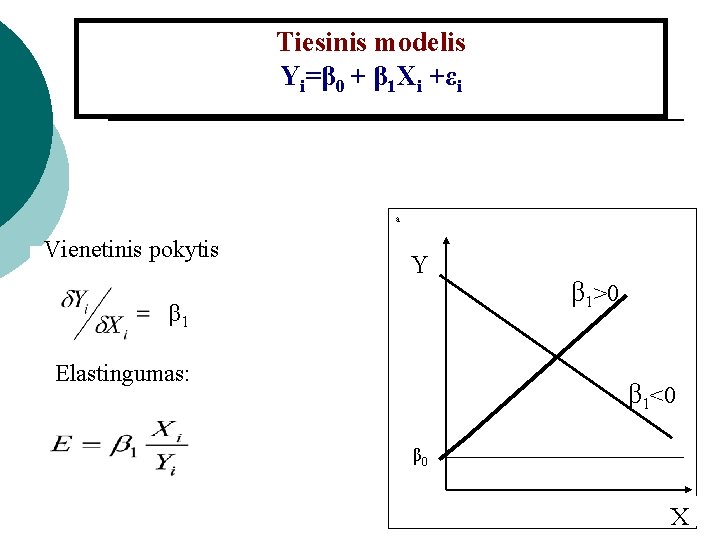
Tiesinis modelis Yi=β 0 + β 1 Xi +εi a Vienetinis pokytis Y β 1 Elastingumas: β 1>0 β 1<0 β 0 X

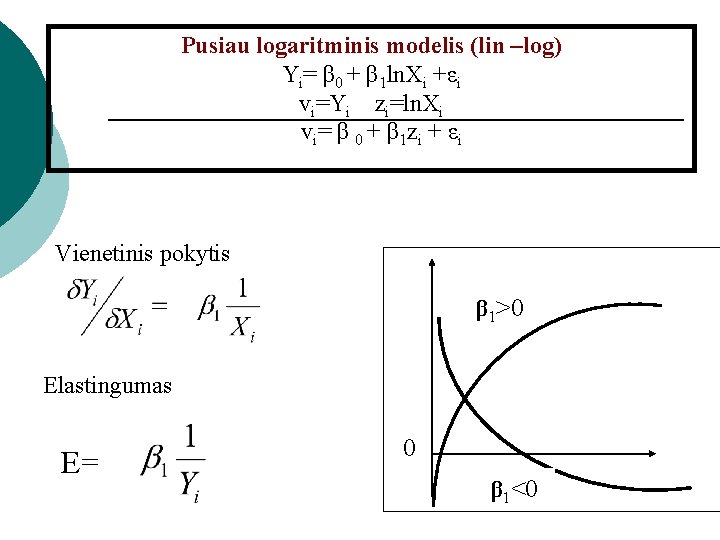
Pusiau logaritminis modelis (lin –log) Yi= β 0 + β 1 ln. Xi +εi vi=Yi zi=ln. Xi vi= β 0 + β 1 zi + εi Vienetinis pokytis β 1>0 Elastingumas E= 0 β 1<0

Eksponentinis modelis (log-lin) ln. Yi=ln(β 0) + β 1 Xi + εi vi=ln(Yi) zi=Xi β’ 0=ln(β 0) vi =β’ 0 + β 1 zi + εi Vienetinis pokytis β Y β 1>0 β 1 Yi Elastingumas E= β 1<0 X

Pvz. Vertinimo funkcija Tiesinė- eksponentinė-logaritminė

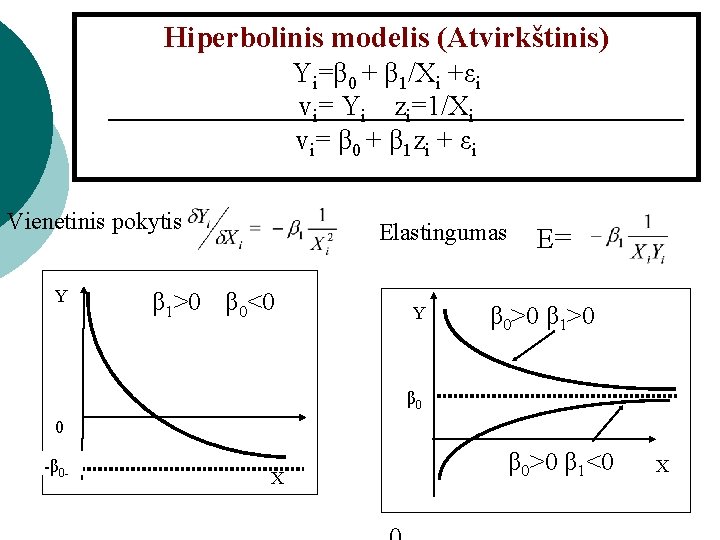
Hiperbolinis modelis (Atvirkštinis) Yi=β 0 + β 1/Xi +εi vi= Yi zi=1/Xi vi= β 0 + β 1 zi + εi Vienetinis pokytis Y Elastingumas β 1>0 β 0<0 Y E= β 0>0 β 1>0 β 0 0 -β 0 - X β 0>0 β 1<0 X

Laipsninis modelis (Log-Log) Yi=β 0 (X i)β 1 expεi ln(Yi)=ln(β 0) + β 1 ln(Xi) + εi vi= ln(Yi ) zi=ln(Xi ) β 0’=ln(b 0) vi = β’ 0 + β 1 zi + εi Vienetinis pokytis b β 1>1 Elastingumas E= 0<β 1<1 β<0

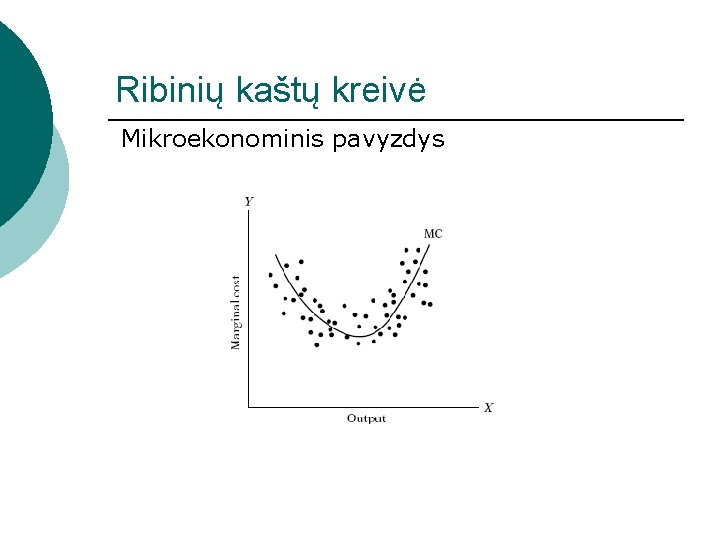
Kvadratinė funkcija Yi=β 0 + β 1 Xi + β 12 Xi 2 +εi Vienetinis pokytis y Elastingumas x

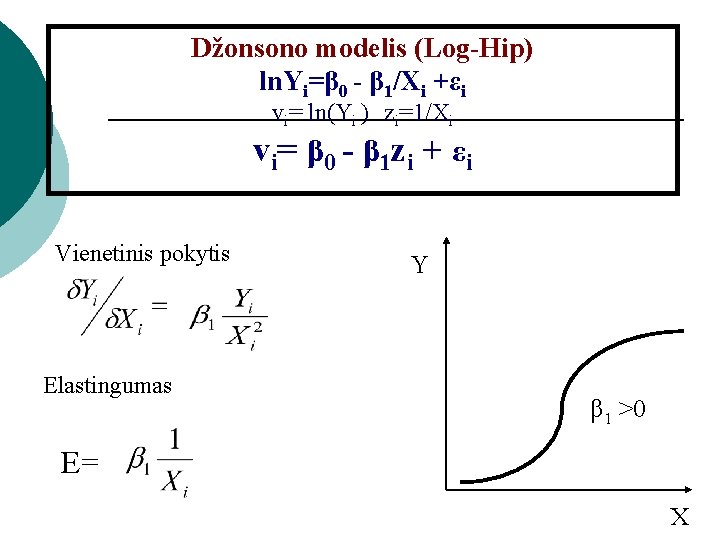
Džonsono modelis (Log-Hip) ln. Yi=β 0 - β 1/Xi +εi vi= ln(Yi ) zi=1/Xi vi= β 0 - β 1 zi + εi Vienetinis pokytis Elastingumas Y β 1 >0 E= X

Modelių taikymo pavyzdžiai Hiperbolinis modelis

Matematinė modelio išraiška v Netiesinis kintamojo X atžvilgiu v Tiesinis koeficientų atžvilgiu

Kai X neaprėžtai didėja: v artėja prie 0; v Y artėja prie asimptotinės reikšmės β 1.

Vienetinis pokytis ir elastingumas Vienetinis pokytis: Interpretacija: X pakitus 1 vnt. , Y pakinta vnt. Elastingumas: Interpretacija: X pakitus 1%, y pakinta %.

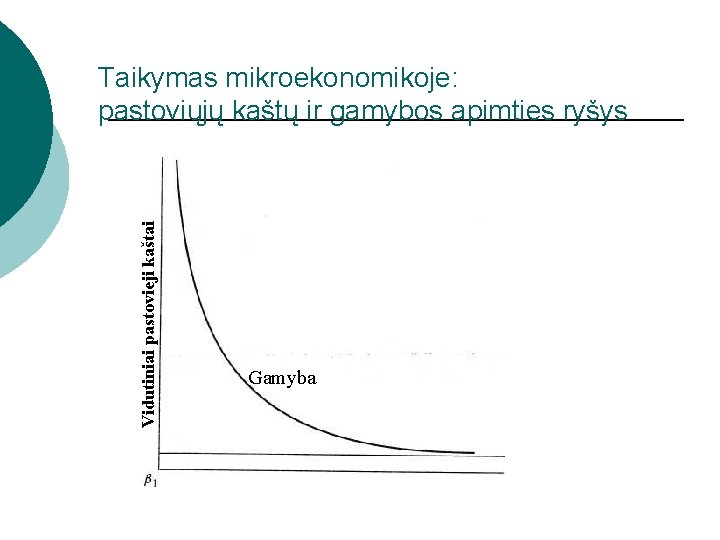
Vidutiniai pastovieji kaštai Taikymas mikroekonomikoje: pastoviųjų kaštų ir gamybos apimties ryšys Gamyba

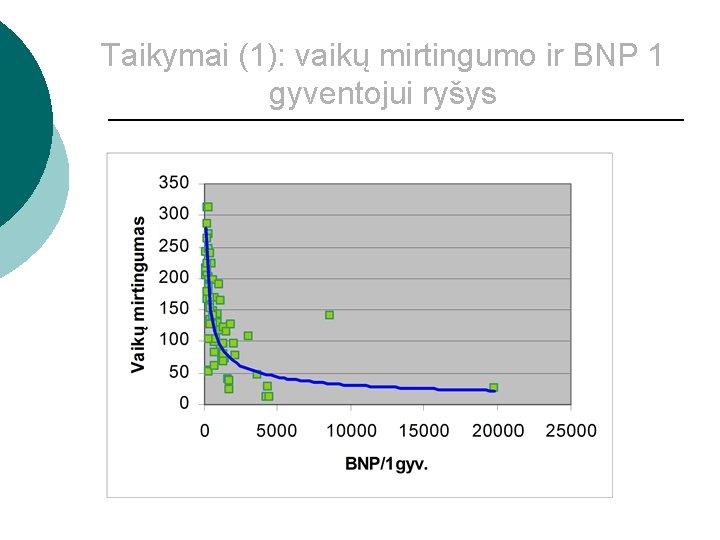
Taikymai (1): vaikų mirtingumo ir BNP 1 gyventojui ryšys

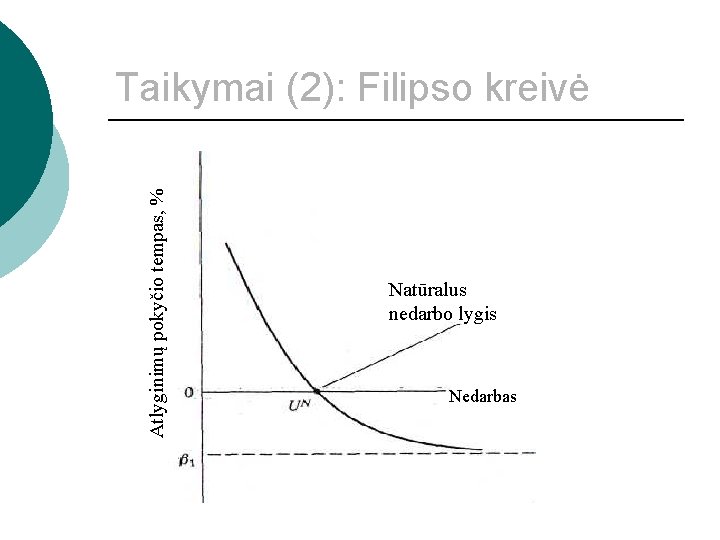
Atlyginimų pokyčio tempas, % Taikymai (2): Filipso kreivė Natūralus nedarbo lygis Nedarbas

Taikymai (2): Filipso kreivė

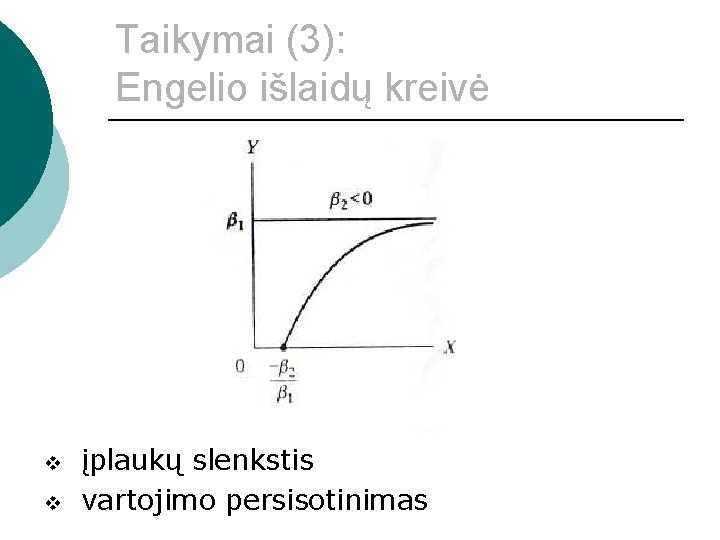
Taikymai (3): Engelio išlaidų kreivė v v įplaukų slenkstis vartojimo persisotinimas

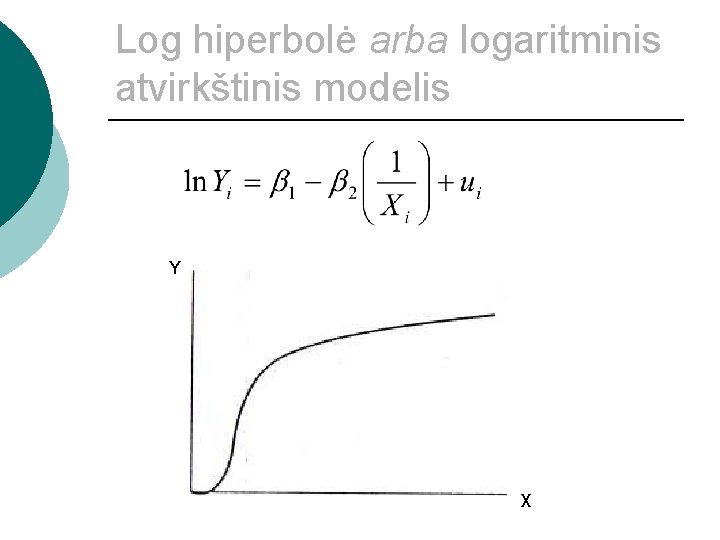
Log hiperbolė arba logaritminis atvirkštinis modelis Y X

¡ Eksponentinis modelis

Thomas Robert Malthus (1766 -1834 m. ) ¡Pirmasis suvokė, kad bet kokių rūšių skaičius gali potencialiai augti skaičiumi, kintančiu pagal geometrinį nuoseklumą. Pvz. : Jei rūšys turi nesutampančias populiacijas (pvz. : kasmetiniai augalai) ir kiekvienas organizmas palieka R palikuonių, populiacijos skaičius N kartose t=0, 1, 2, . . . yra lygus: N 1=N 0×R Nt =N 0×Rt 1 pav. , T. R. Malthus Kai t yra didelis, tai ši formulė gali būti prilyginta eksponentinei funkcijai:

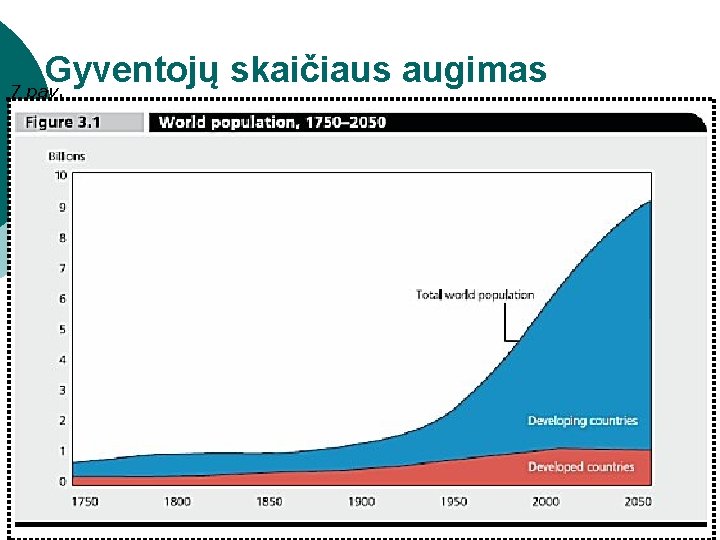
Gyventojų skaičiaus augimas 7 pav.

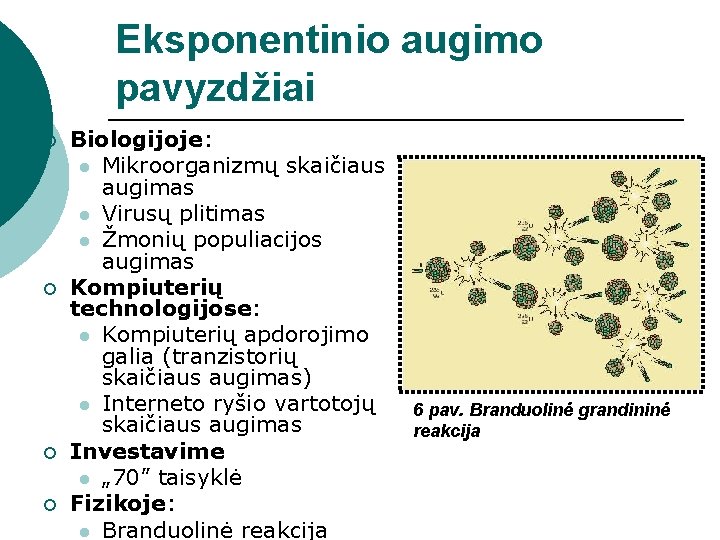
Eksponentinio augimo pavyzdžiai ¡ ¡ Biologijoje: l Mikroorganizmų skaičiaus augimas l Virusų plitimas l Žmonių populiacijos augimas Kompiuterių technologijose: l Kompiuterių apdorojimo galia (tranzistorių skaičiaus augimas) l Interneto ryšio vartotojų skaičiaus augimas Investavime l „ 70” taisyklė Fizikoje: l Branduolinė reakcija 6 pav. Branduolinė grandininė reakcija

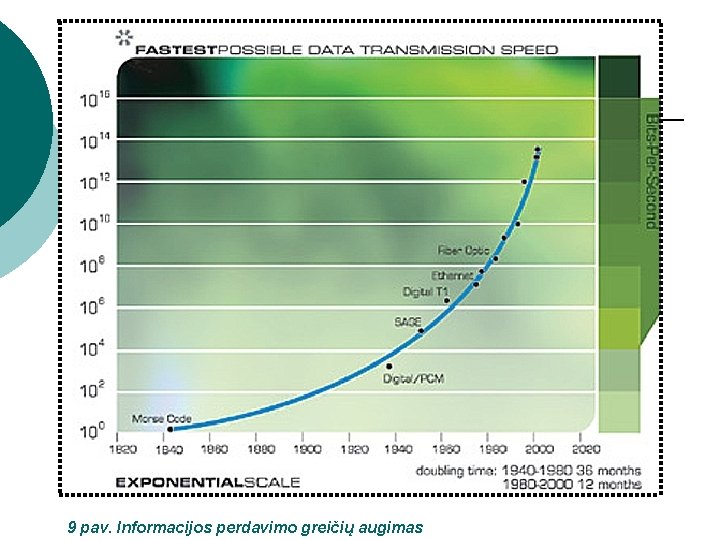
9 pav. Informacijos perdavimo greičių augimas

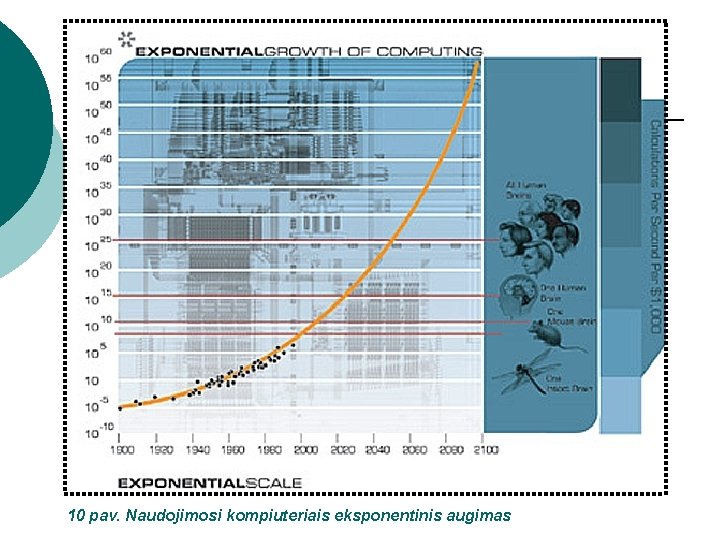
10 pav. Naudojimosi kompiuteriais eksponentinis augimas

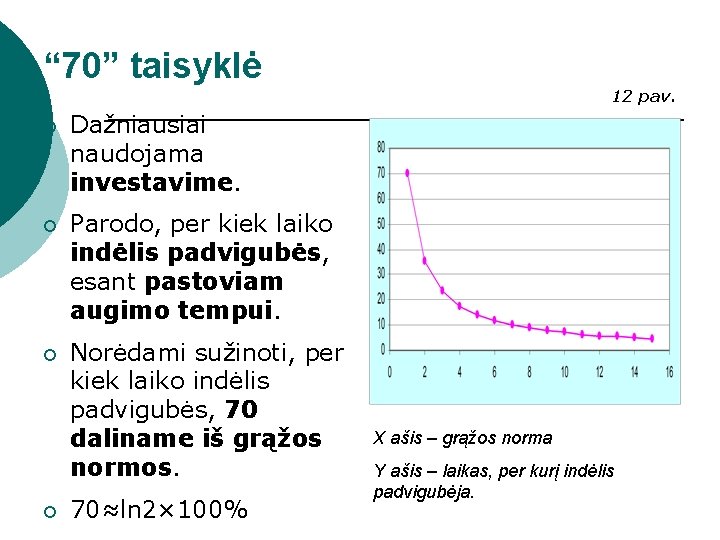
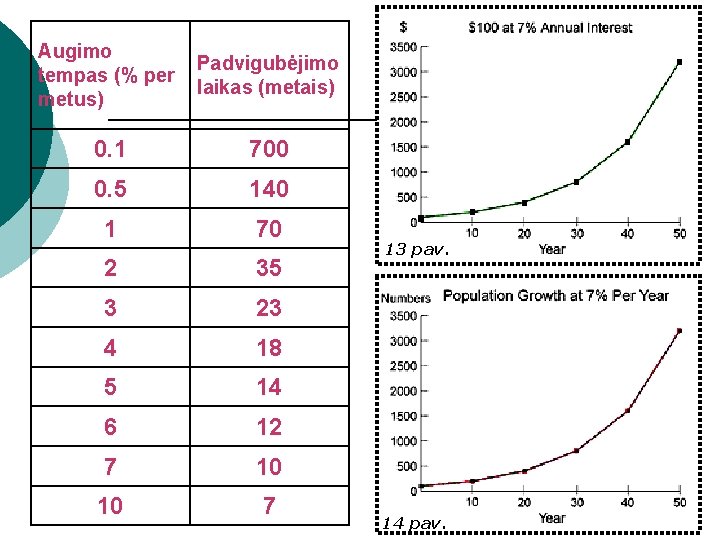
“ 70” taisyklė 12 pav. ¡ Dažniausiai naudojama investavime. ¡ Parodo, per kiek laiko indėlis padvigubės, esant pastoviam augimo tempui. ¡ Norėdami sužinoti, per kiek laiko indėlis padvigubės, 70 daliname iš grąžos normos. ¡ 70≈ln 2× 100% X ašis – grąžos norma Y ašis – laikas, per kurį indėlis padvigubėja.

Augimo tempas (% per metus) Padvigubėjimo laikas (metais) 0. 1 700 0. 5 140 1 70 2 35 3 23 4 18 5 14 6 12 7 10 10 7 13 pav. 14 pav.

Šachmatų lenta ir ryžiai (1) Kartą Persijos karalius dovanų gavo rankų darbo šachmatų lentą. Paklausęs meistro, padariusio lentą, kokio atpildo jis norįs, šis atsakęs, jog norėtų: ¡ vieno ryžių grūdelio ant pirmo šachmatų langelio; ¡ dviejų – antro; ¡ keturių – ant trečio ir t. t. 15 pav. * Šachmatų lentoje yra 8× 8=64 langeliai

Šachmatų lenta ir ryžiai (2) Galiausiai viso pasaulio ryžių nebūtų užtekę, norint patenkinti dvariškio prašymą. . . Karalius liko be savo karalystės. . . ☺ 16 pav.

Laipsninis modelis (Log–Log) Donata Jaglinska Sandra Radionovaitė,

Laipsninis modelis (Log – Log) Yi=β 0(Xi)β 1 expεi ln(Yi)=ln(β 0)+ β 1 ln(Xi)+εi Vi= ln(Yi) , zi=ln(Xi) β 0= ln(β 0) , V i = β 0 + β 1 z i + ε i

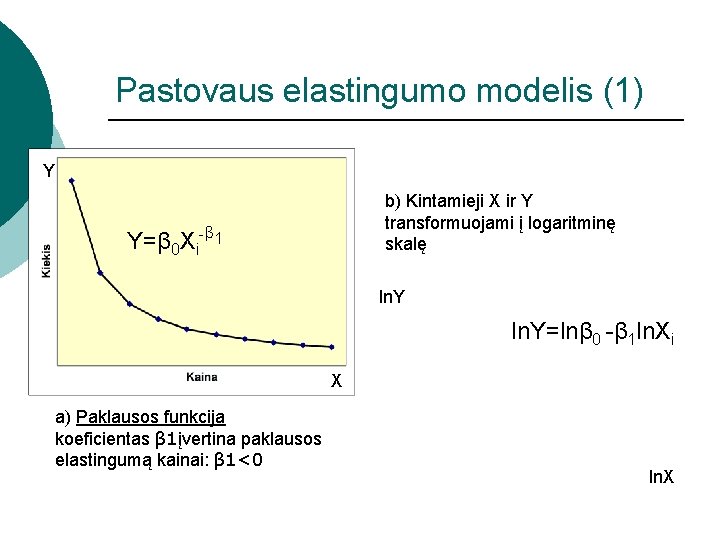
Pastovaus elastingumo modelis (1) Y b) Kintamieji X ir Y transformuojami į logaritminę skalę Y=β 0 Xi-β 1 ln. Y=lnβ 0 -β 1 ln. Xi X a) Paklausos funkcija koeficientas β 1įvertina paklausos elastingumą kainai: β 1<0 ln. X

Pastovaus elastingumo modelis (1) ¡ ¡ Laipsninis modelis dažnai vadinamas pastovaus elastingumo modeliu, kadangi elastingumo koeficientas tarp X ir Y (β 1) visąlaik išlieka pastovus, nesvarbu, kuriame taške jį skaičiuotume. Paklausos funkcijos atveju pastovaus elastingumo modelis parodo pastovų kiekio pokytį esant duotam procentiniam kainos pokyčiui, nepaisant absoliutaus kainų lygio.

Gamybos funkcija – laipsninio modelio pavyzdys ¡ Pastovaus elastingumo substitucinė gamybos funkcija – CES (angl. constant elasticity of subtitution): log(V/L)=logβ 0+β 1 log. W+ε kur V/L – pridėtinė vertė, tenkanti 1 darbo vienetui; L – darbo sąnaudos; W – realusis darbo užmokestis. Ši funkcija įvertina pakeičiamumo tarp darbo ir kapitalo sąnaudų elastingumą, kurį parodo parametras β 1.

Gamybos funkcija – laipsninio modelio pavyzdys ¡ Cobb-Douglas (substitucinė) gamybos funkcija: Y=f(K, L) K – kapitalas; L –darbas. α 1 -α Y=KL α – kapitalo lyginamasis svoris; 1 - α – darbo lyginamasis svoris.

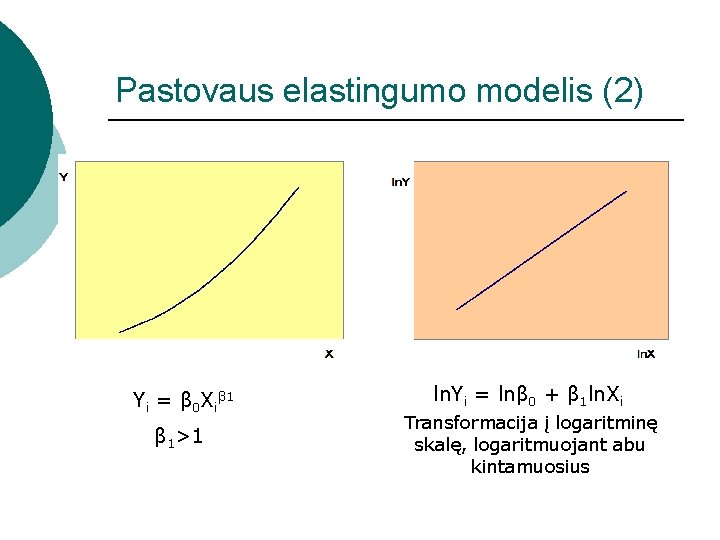
Pastovaus elastingumo modelis (2) Yi = β 0 Xiβ 1 β 1>1 ln. Yi = lnβ 0 + β 1 ln. Xi Transformacija į logaritminę skalę, logaritmuojant abu kintamuosius

Kvadratinė funkcija Jurgita Petkelytė Akvilė Ignotaitė

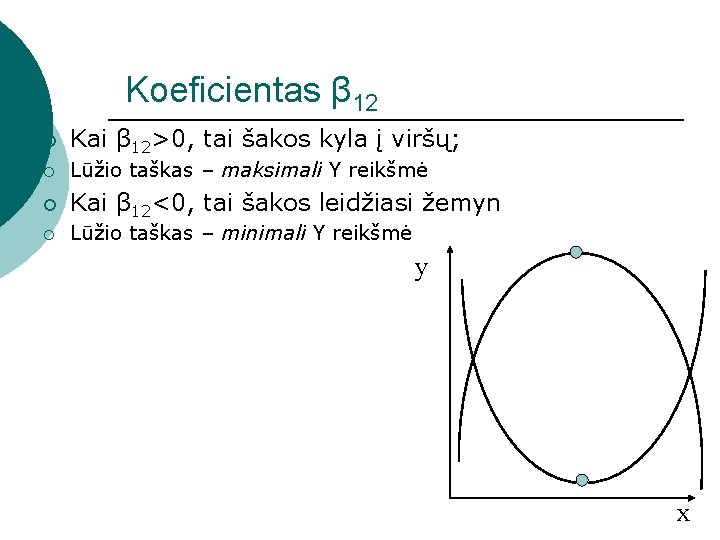
Koeficientas β 12 ¡ Kai β 12>0, tai šakos kyla į viršų; ¡ Lūžio taškas – maksimali Y reikšmė ¡ Kai β 12<0, tai šakos leidžiasi žemyn ¡ Lūžio taškas – minimali Y reikšmė y x

Ribinių kaštų kreivė Mikroekonominis pavyzdys

Laferio kreivė Makroekonominis pavyzdys

Logaritmuotų kintamųjų įverčių interpretacija Funkcija Matematinė išraiška Interpretacija Lin-log β 1 /100 - parodo, kiek vienetų pasikeičia Y, jeigu X pakinta 1 procentu Log-lin 100. β 1 - parodo, kiek procentų pasikeičia Y, jeigu X pakinta 1 vienetu Log-log β 1 - parodo, kiek procentų pasikeičia Y, jeigu X pakinta 1 procentu Log-atvirkšt. 100. β 1 ∙(-1/X 2) - parodo, kiek procentų pasikeičia Y, jeigu X pakinta 1 vienetu

Ln naudojimo ypatumai regresiniuose modeliuose Išlygina duomenų sklaidą ¡ Netiesinę veiksnių saveiką pakeičia tiesine ¡ Logaritmuojant absoliutūs pokyčiai pakeičiami procentiniais pokyčiais ¡

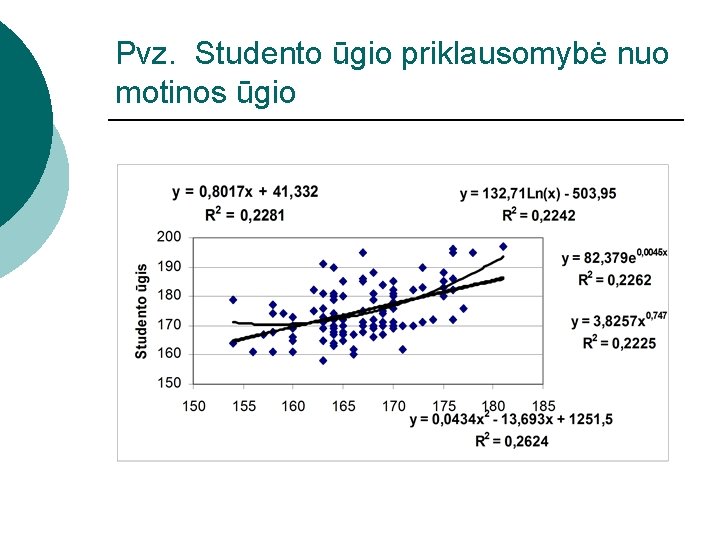
Pvz. Studento ūgio priklausomybė nuo motinos ūgio

Pvz. Studento ūgio priklausomybė nuo tėvo ūgio

Dauginės regresijos kintamųjų matematinė išraiška ¡ ¡ Dauginės regresijos priklausomas kintamasis į regresijos lygtį dažniausiai įtraukiamas tiesine arba logaritmine forma Dauginės regresijos nepriklausomi kintamieji į regresijos lygtį gali būti įtraukiami tiesine, atvirkštine, laipsnine arba logaritmine forma Nepriklausomi kintamieji regresijos lygtyje gali būti skirtingų matematinių formų Fiktyvūs (pseudo-kintamieji) į regresijos lygtį įtraukiami tik tiesine forma

Dauginės regresijos kintamųjų matematinė išraiška (PVZ) Tiesinė priklausomybė Adj R 2= 0, 27 Log-log priklausomybė Adj R 2= 0, 28 Log-lin priklausomybė Adj R 2= 0, 27 Lin-log priklausomybė Adj R 2= 0, 27

Matematinė modelio formos parinkimo kriterijai 1. Priklausomas kintamasis tos pačios matematinės formos a) Lyginti koreguotus determinacijos koeficientus 2. Priklausomas kintamasis skirtingos matematinės formos a) Taikome Zarembka testą

Zarembka testas Tarkim turime dvi regresijas: ir Box-Cox transformacija Palyginame determinacijos koeficientus R 2 dviejų regresijos lygčių Didesnis determinacijos koeficientas parodo, kuri matematinė forma geriau aprašo priklausomybę.

Papildomos analizės galimybės ¡ ¡ ¡ Veiksnių įtakos poveikio palyginimas (standartizuotų kintamųjų regresija) Pokyčių analizė Struktūrinių pokyčių analizė

Pokyčių naudojimo ypatumai Tik laiko eilučių duomenims ¡ Išeliminuoja vienetinę šaknį, t. y, augimo trendą. ¡ Mažesnė melagingos koreliacijos tikimybė. ¡ Patikimesnis sąryšio įvertinimas ¡

Papildomos analizės galimybės ¡ Struktūrinių pokyčių analizė l Chow testas ¡ H 0 struktūrinis stabilumas ¡ HA struktūrinis pokytis ¡ Testo statistika: l Hipotezės atmetimo taisyklė; ¡ Chow_stat >F( α, k, n 1+ n 2+2 k) Atmetama H 0