REGRESI DAN KORELASI SEDERHANA UDIN NASHRUDDIN S Si










- Slides: 15

REGRESI DAN KORELASI SEDERHANA UDIN NASHRUDDIN, S. Si. AMIK AL MASOEM udinnashruddin. mm. almasoem@gmail. com

REGRESI Bentuk persamaan yang sesuai jika terdapat minimal dua variabel yang diamati. Persamaan tersebut digunakan untuk meramal (predict) rata-rata satu variabel terhadap variabel lainnya. Dari dua variabel tersebut ada yang variabel yang menentukan nilai variabel lainnya, variabel demikian dinamakan variabel bebas (independent). Sedangkan variabel yang ditentukan nilainya oleh variabel lain disebut variabel tidak bebas (dependent)

�Pada kasus tingginya suku bunga pinjaman akan mempengaruhi besarnya pinjaman nasabah terhadap perusahaan jasa keuangan. �Dalam hal ini suku bunga adalah variabel bebas/penentu/independent, karena suku bunga pinjaman mempengaruhi varabel lain yaitu besaran pinjaman nasabah terhadap penyedia jasa keuangan. �Sedangkan besaran pinjaman nasabah sangat dipengaruhi oleh tingkat suku bunga dalam hal ini besaran pinjaman nasabah adalah variabel yang nilainya sangat tergantung pada variabel lain (tingkat suku bunga), sehingga variabel besaran pinjaman disebut variabel tidak bebas/dependent/ditentukan

�Variabel bebas/independent biasanya dinyatakan oleh X sedangkan variabel tidak bebas/dependent biasanya dinyatakan oleh Y �Hubungan antara variabel bebas dengan variabel tidak bebas biasanya dinyatakan dalam model persamaan matematika yang berupa garis lurus/linear. �Garis linear/regresi yang dimaksud merupakan garis penaksir (estimating line) dari setiap titik koordinat yang menghubungkan kedua variabel.

�Contoh Penerapan Analisis Regresi 1. 2. 3. 4. 5. 6. Analisis Regresi antara tinggi orang tua terhadap tinggi anaknya (Gultom). Analisis Regresi antara pendapatan terhadap konsumsi rumah tangga. Analisis Regresi antara harga terhadap penjualan barang. Analisis Regresi antara tingkat upah terhadap tingkat pengangguran. Analisis Regresi antara tingkat suku bunga bank terhadap harga saham Analisis regresi antara biaya periklanan terhadap volume penjualan perusahaan.

Regresi

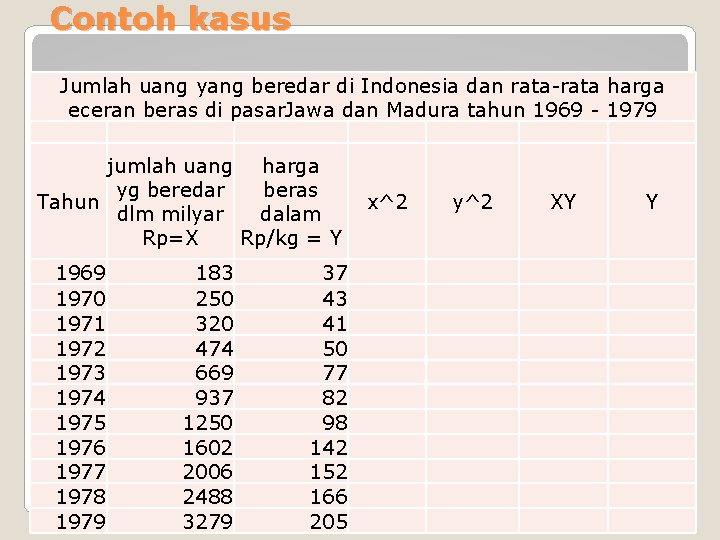
Contoh kasus Jumlah uang yang beredar di Indonesia dan rata-rata harga eceran beras di pasar. Jawa dan Madura tahun 1969 - 1979 jumlah uang harga yg beredar beras Tahun dlm milyar dalam Rp=X Rp/kg = Y 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 183 250 320 474 669 937 1250 1602 2006 2488 3279 37 43 41 50 77 82 98 142 152 166 205 x^2 y^2 XY

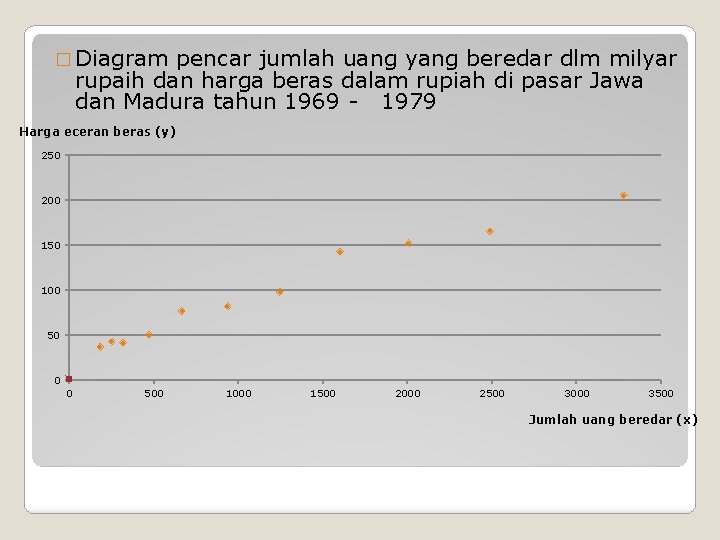
� Diagram pencar jumlah uang yang beredar dlm milyar rupaih dan harga beras dalam rupiah di pasar Jawa dan Madura tahun 1969 - 1979 Harga eceran beras (y) 250 200 150 100 50 0 0 500 1000 1500 2000 2500 3000 3500 Jumlah uang beredar (x)

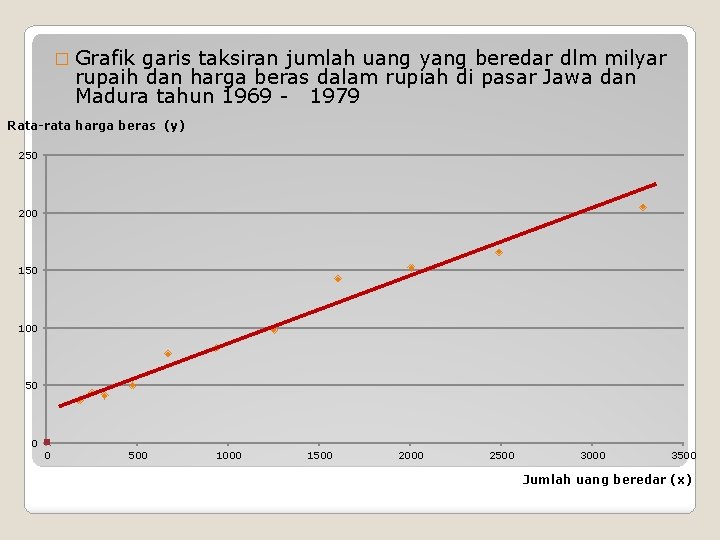
� Grafik garis taksiran jumlah uang yang beredar dlm milyar rupaih dan harga beras dalam rupiah di pasar Jawa dan Madura tahun 1969 - 1979 Rata-rata harga beras (y) 250 200 150 100 50 0 0 500 1000 1500 2000 2500 3000 3500 Jumlah uang beredar (x)

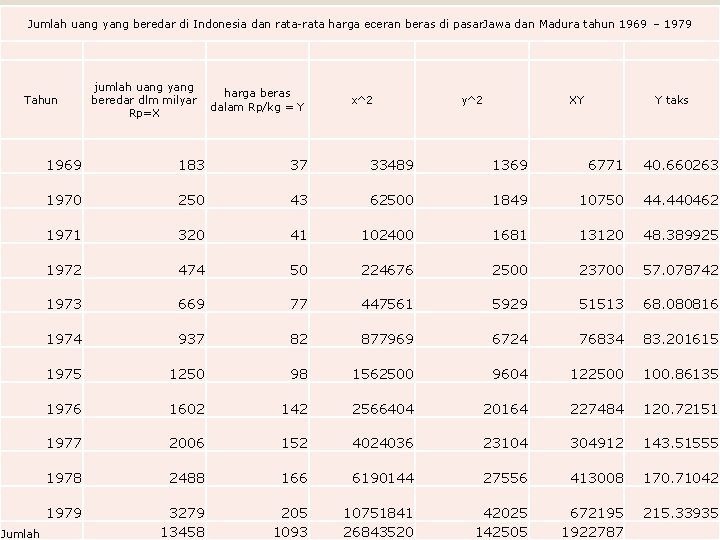
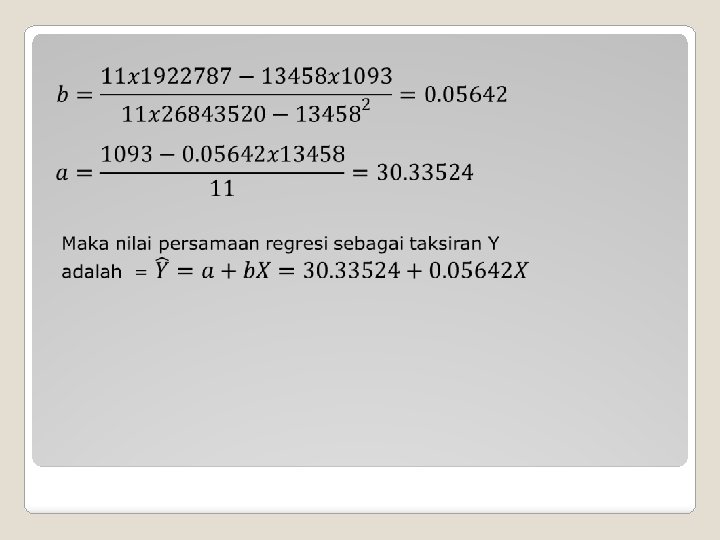
Jumlah uang yang beredar di Indonesia dan rata-rata harga eceran beras di pasar. Jawa dan Madura tahun 1969 – 1979 Tahun Jumlah jumlah uang yang harga beras beredar dlm milyar dalam Rp/kg = Y Rp=X x^2 y^2 XY Y taks 1969 183 37 33489 1369 6771 40. 660263 1970 250 43 62500 1849 10750 44. 440462 1971 320 41 102400 1681 13120 48. 389925 1972 474 50 224676 2500 23700 57. 078742 1973 669 77 447561 5929 51513 68. 080816 1974 937 82 877969 6724 76834 83. 201615 1975 1250 98 1562500 9604 122500 100. 86135 1976 1602 142 2566404 20164 227484 120. 72151 1977 2006 152 4024036 23104 304912 143. 51555 1978 2488 166 6190144 27556 413008 170. 71042 1979 3279 13458 205 1093 10751841 26843520 42025 142505 672195 215. 33935 1922787


�CONTOH KASUS Seorang manajer pemasaran akan meneliti apakah terdapat pengaruh iklan terhadap penjualan pada perusahaan-perusahaan di Kabupaten Sweet. Water, untuk kepentingan penelitian tersebut diambil 8 perusahaan sejenis yang telah melakukan promosi. Data yang dikumpulkan adalah sebagai berikut: Penjualan (Y) 64 61 84 70 88 92 72 77 Promosi (X) 20 16 34 23 27 32 18 22

�Analisis data Untuk analisis data diperlukan, perhitungan: 1. Persamaan regresi 2. Nilai Prediksi 3. Kesimpulan


�KORELASI SEDERHANA