REGRESI DAN KORELASI REGRESI Analisis regresi dalam statistika

REGRESI DAN KORELASI

REGRESI Analisis regresi dalam statistika adalah satu metode untuk menentukan hubungan sebab-akibat antara satu variabel dengan variabel(-variabel) yang lain • Gagasan perhitungan ditetapkan oleh Sir Francis Galton (1822 -1911) • Persamaan regresi: Persamaan matematik yang memungkinkan peramalan nilai suatu peubah tak-bebas (dependent variable) dari nilai peubah bebas (independent variable) • Diagram Pencar = Scatter Diagram yang menggambarkan persebaran nilai-nilai observasi peubah takbebas dan peubah bebas. Nilai peubah bebas : ditulis pada sumbu X (sumbu horizontal) Nilai peubah takbebas : ditulis pada sumbu Y (sumbu vertikal) Nilai peubah tak-bebas ditentukan oleh nilai peubah bebas Contoh : Umur vs Tinggi tanaman Biaya Promosi vs Volume penjualan Vol. Penjualan) (X : umur, Y : Tinggi tanaman) (X : Biaya Promosi, Y :

Jenis-jenis Persamaan Regresi : a. Regresi Linier : - Regresi Linier Sederhana Bentuk Umum : - Regresi Linier Berganda Bentuk Umum : Y X 1 X 2 Xn : Peubah Tak bebas : Peubah bebas ke-1 : Peubah bebas ke-2 : Peubah bebas ke-n b. Regresi Non Linier : - Regresi Eksponensial Bentuk Umum : Y X a b Y = a + b. X : Peubah Tak bebas : Peubah bebas : Konstanta : Kemiringan Y = a + b 1 X 1 + b 2 X 2 +. . . + bn. Xn a b 1 b 2 bn : Konstanta : kemiringan garis ke-1 : kemiringan garis ke-2 : kemiringan garis ke-n Y = abx Log Y = log a + (log b) X

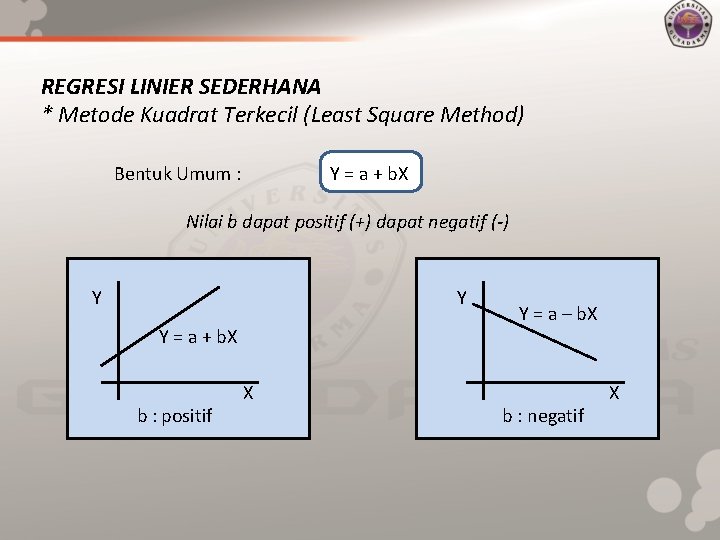
REGRESI LINIER SEDERHANA * Metode Kuadrat Terkecil (Least Square Method) Bentuk Umum : Y = a + b. X Nilai b dapat positif (+) dapat negatif (-) Y Y Y = a + b. X b : positif X Y = a – b. X b : negatif X

PENETAPAN PERSAMAAN REGRESI LINIER SEDERHANA Sehingga

CONTOH Berikut adalah data Biaya Promosi dan Volume Penjualan PT BIMOIL perusahaan Minyak Gosok. Tentukan persamaan Regresinya Tahun X Biaya Promosi (Jutaan Rupiah) Y Volume Penjualan (Ratusan Juta Liter) 1992 2 5 1993 4 6 1994 5 8 1995 7 10 1996 8 11 XY X 2 Y 2 Jumlah Silakan diselesaikan

PERAMALAN DENGAN PERSAMAAN REGRESI Contoh : Diketahui hubungan Biaya Promosi (X dalam Juta Rupiah) dan Y (Volume penjualan dalam Ratusan Juta liter) dapat dinyatakan dalam persamaan regresi linier berikut : Y = 2, 530 + 1, 053 X Perkirakan Volume penjualan jika, dikeluarkan biaya promosi Rp. 10 juta? Jawab : Y = 2, 530 + 1, 053 X X = 10 Y = 2, 53 + 1, 053 (10) = 2, 53 + 10, 53 = 13, 06 (ratusan juta liter) Volume penjualan = 13. 06 x 100 000 liter

Korelasi linier sederhana korelasi, juga disebut koefisien korelasi, adalah nilai yang menunjukkan kekuatan dan arah hubungan linier antara dua peubah acak (random variable). Koefisien Korelasi (r): ukuran hubungan linier peubah X dan Y Nilai r berkisar antara (+1) sampai (– 1) Nilai r yang (+) ditandai oleh nilai b yang (+) Nilai r yang (-) ditandai oleh nilai b yang (–) Jika nilai r mendekati +1 atau r mendekati – 1 maka X dan Y memiliki korelasi linier yang tinggi. Jika nilai r = +1 atau r = – 1 maka X dan Y memiliki korelasi linier sempurna. Jika nilai r = 0 maka X dan Y tidak memiliki relasi (hubungan) linier (dalam kasus r mendekati 0, anda dapat melanjutkan analisis ke regresi eksponensial). Koefisien Determinasi Sampel = R = r² Ukuran proporsi keragaman total nilai peubah Y yang dapat dijelaskan oleh nilai peubah X melalui hubungan linier.

koefisien korelasi dan determinasi Lihat Contoh sebelumnya, setelah mendapatkan persamaan Regresi Y = 2. 530 + 1. 053 X, hitung koefisien korelasi (r) dan koefisien determinasi (R). r= R= 0, 9857. . . 0, 97165. . . = 97% Nilai R = 97% menunjukkan bahwa 97% proporsi keragaman nilai peubah Y (volume penjualan) dapat dijelaskan oleh nilai peubah X (biaya promosi) melalui hubungan linier. Sisanya, yaitu 3 % dijelaskan oleh hal-hal lain.

Regresi linier berganda Pembahasan akan meliputi regresi linier dengan 2 Variabel Bebas (X 1 dan X 2) dan 1 Variabel Tak Bebas (Y). • Bentuk Umum : Y : peubah tak-bebas X 1 : peubah bebas ke-1 X 2 : peubah bebas ke-2 Y = a + b 1 X 1 + b 2 X 2 a : konstanta b 1 : kemiringan garis ke-1 b 2 : kemiringan garis ke-2 a , b 1 dan b 2 didapatkan dengan menyelesaikan tiga persamaan Normal berikut: n : banyaknya pasangan data X 1 i : nilai peubah bebas X 1 ke-i yi : nilai peubah bebas Y ke-i x 2 i : nilai peubah bebas X 2 ke-i

Contoh 5: Berikut adalah data Volume Penjualan (juta unit) mobil dihubungkan dengan variabel biaya promosi (X 1 dalam juta rupiah/tahun) dan variabel biaya penambahan asesoris (X 2 dalam ratusan ribu rupiah/unit). Tetapkan persamaan Regresi Linier Berganda Y = a + b 1 X 1 + b 2 X 2 x 1 x 2 y 2 3 4 5 5 6 8 10 7 9 11 8 10 12 31 40 50 x 1 x 2 x 1 y x 2 y x 12 x 22 y 2 239 296 379 187 306 470

Masukkan hasil tabel dalam ketiga persamaan normal : Diperoleh Persamaan Regresi Berganda : 0, 75 + 0, 50 X 1 + 0, 75 X 2

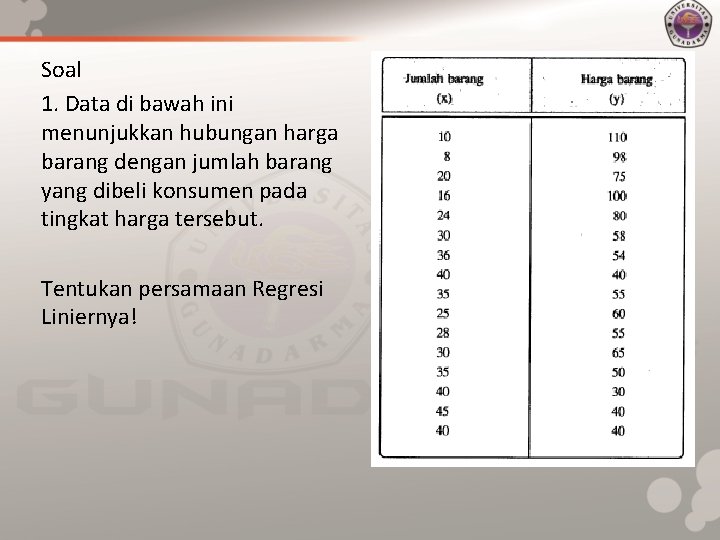
Soal 1. Data di bawah ini menunjukkan hubungan harga barang dengan jumlah barang yang dibeli konsumen pada tingkat harga tersebut. Tentukan persamaan Regresi Liniernya!

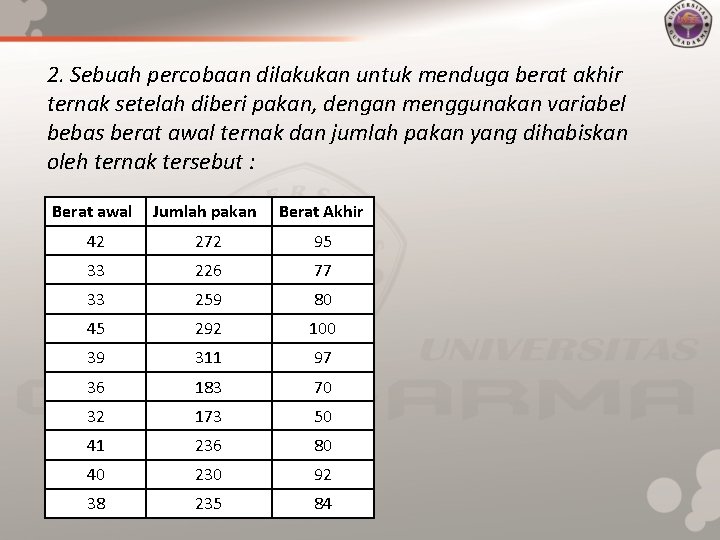
2. Sebuah percobaan dilakukan untuk menduga berat akhir ternak setelah diberi pakan, dengan menggunakan variabel bebas berat awal ternak dan jumlah pakan yang dihabiskan oleh ternak tersebut : Berat awal Jumlah pakan Berat Akhir 42 272 95 33 226 77 33 259 80 45 292 100 39 311 97 36 183 70 32 173 50 41 236 80 40 230 92 38 235 84

Terima Kasih