RegisterTransfer Level RTL Design Recall Chapter 2 Combinational

Register-Transfer Level (RTL) Design • Recall – Chapter 2: Combinational Logic Design • First step: Capture behavior (using equation or truth table) • Remaining steps: Convert to circuit – Chapter 3: Sequential Logic Design Capture behavior • First step: Capture behavior (using FSM) • Remaining steps: Convert to circuit • RTL Design (the method for creating custom processors) Convert to circuit – First step: Capture behavior (using highlevel state machine, to be introduced) – Remaining steps: Convert to circuit 1

RTL Design Method 2

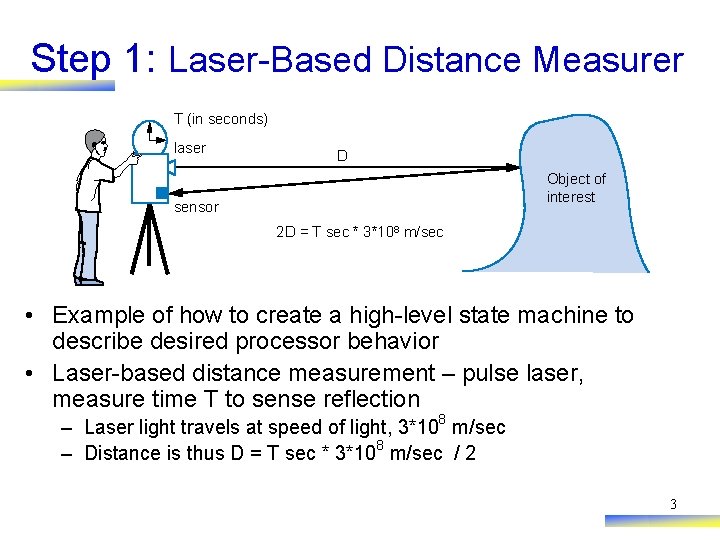
Step 1: Laser-Based Distance Measurer T (in seconds) laser D Object of interest sensor 2 D = T sec * 3*108 m/sec • Example of how to create a high-level state machine to describe desired processor behavior • Laser-based distance measurement – pulse laser, measure time T to sense reflection – Laser light travels at speed of light, 3*108 m/sec – Distance is thus D = T sec * 3*108 m/sec / 2 3

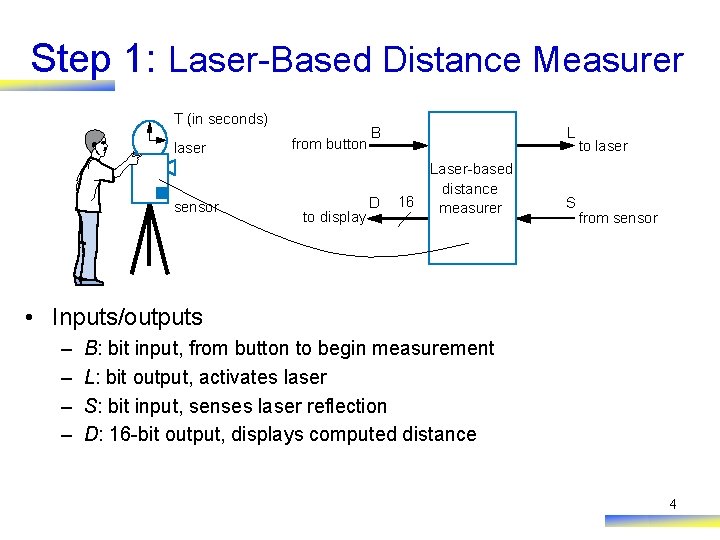
Step 1: Laser-Based Distance Measurer T (in seconds) laser sensor from button to display B D L 16 Laser-based distance measurer S to laser from sensor • Inputs/outputs – – B: bit input, from button to begin measurement L: bit output, activates laser S: bit input, senses laser reflection D: 16 -bit output, displays computed distance 4

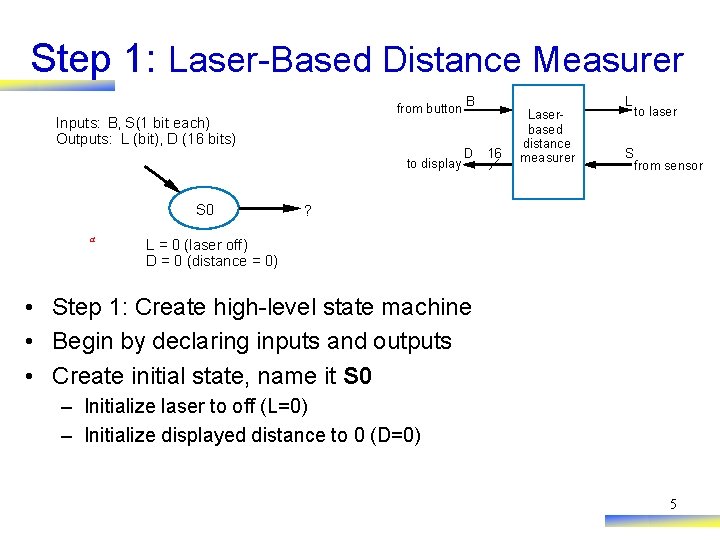
Step 1: Laser-Based Distance Measurer from button B Inputs: B, S(1 bit each) Outputs: L (bit), D (16 bits) to display S 0 a D 16 Laserbased distance measurer L S to laser from sensor ? L = 0 (laser off) D = 0 (distance = 0) • Step 1: Create high-level state machine • Begin by declaring inputs and outputs • Create initial state, name it S 0 – Initialize laser to off (L=0) – Initialize displayed distance to 0 (D=0) 5

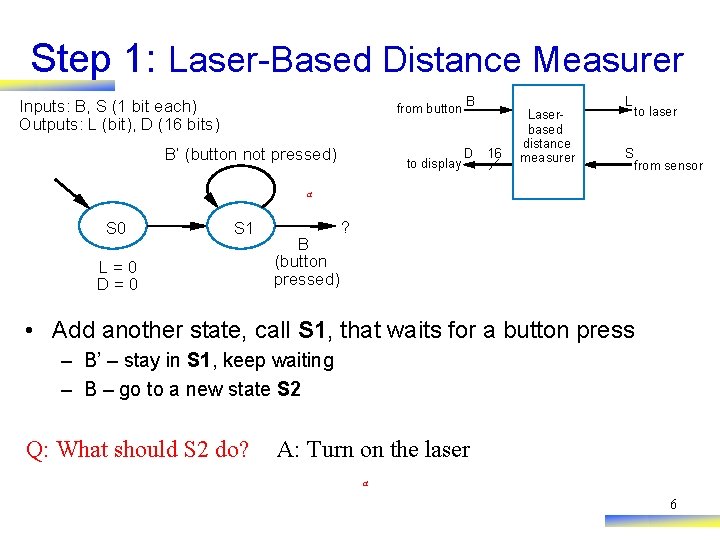
Step 1: Laser-Based Distance Measurer from button B Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) B’ (button not pressed) to display D 16 Laserbased distance measurer L S to laser from sensor a S 0 S 1 L=0 D=0 B (button pressed) ? • Add another state, call S 1, that waits for a button press – B’ – stay in S 1, keep waiting – B – go to a new state S 2 Q: What should S 2 do? A: Turn on the laser a 6

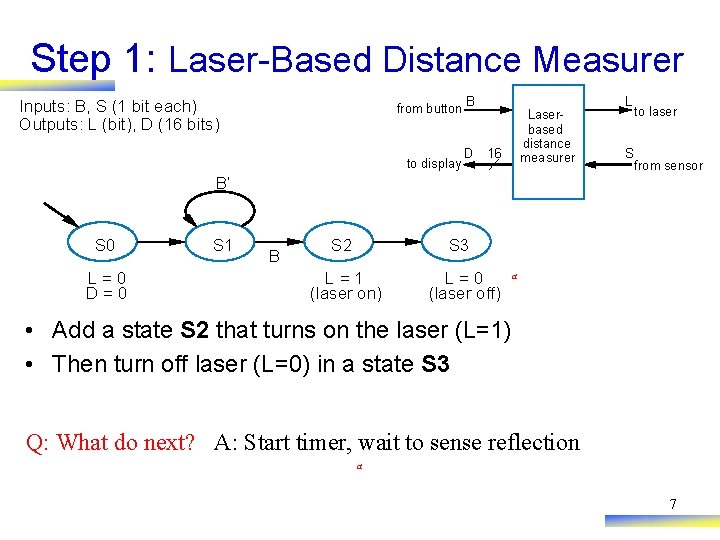
Step 1: Laser-Based Distance Measurer from button B Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) to display D Laserbased distance measurer 16 L S to laser from sensor B’ S 0 L=0 D=0 S 1 B S 2 S 3 L=1 (laser on) L=0 (laser off) a • Add a state S 2 that turns on the laser (L=1) • Then turn off laser (L=0) in a state S 3 Q: What do next? A: Start timer, wait to sense reflection a 7

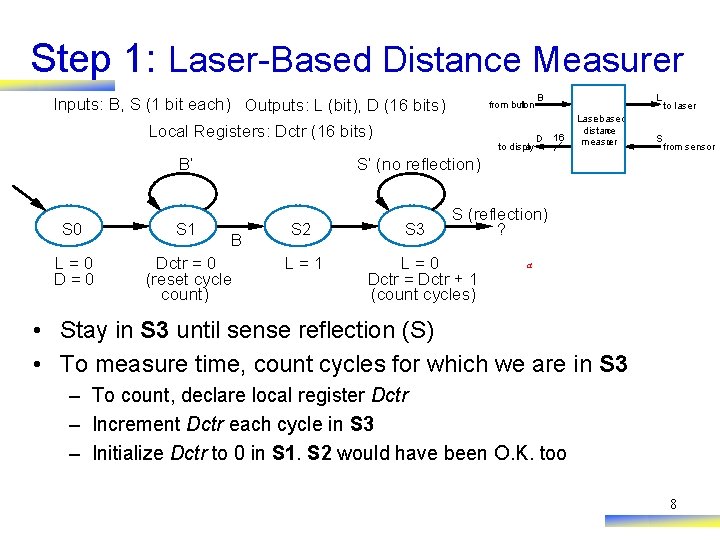
Step 1: Laser-Based Distance Measurer Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) from button Local Registers: Dctr (16 bits) to display B’ B D L 16 Lase r-based distance measu rer S to laser from sensor S’ (no reflection) S 0 S 1 L=0 Dctr = 0 (reset cycle count) B S 2 L=1 S 3 S (reflection) ? L=0 Dctr = Dctr + 1 (count cycles) a • Stay in S 3 until sense reflection (S) • To measure time, count cycles for which we are in S 3 – To count, declare local register Dctr – Increment Dctr each cycle in S 3 – Initialize Dctr to 0 in S 1. S 2 would have been O. K. too 8

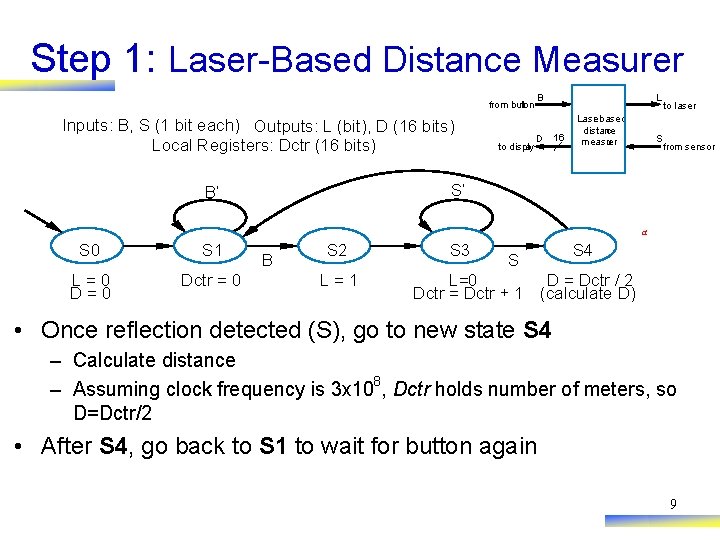
Step 1: Laser-Based Distance Measurer from button Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) Local Registers: Dctr (16 bits) to display B D L 16 Lase r-based distance measu rer S to laser from sensor S’ B’ a S 0 S 1 L=0 Dctr = 0 B S 2 L=1 S 3 S S 4 L=0 D = Dctr / 2 Dctr = Dctr + 1 (calculate D) • Once reflection detected (S), go to new state S 4 – Calculate distance – Assuming clock frequency is 3 x 108, Dctr holds number of meters, so D=Dctr/2 • After S 4, go back to S 1 to wait for button again 9

Step 2: Create a Datapath • Datapath must – Implement data storage – Implement data computations • Look at high-level state machine, do three substeps – (a) Make data inputs/outputs be datapath inputs/outputs – (b) Instantiate declared registers into the datapath (also instantiate a register for each data output) – (c) Examine every state and transition, and instantiate datapath components and connections to implement any data computations Instantiate: to introduce a new component into a design. 10

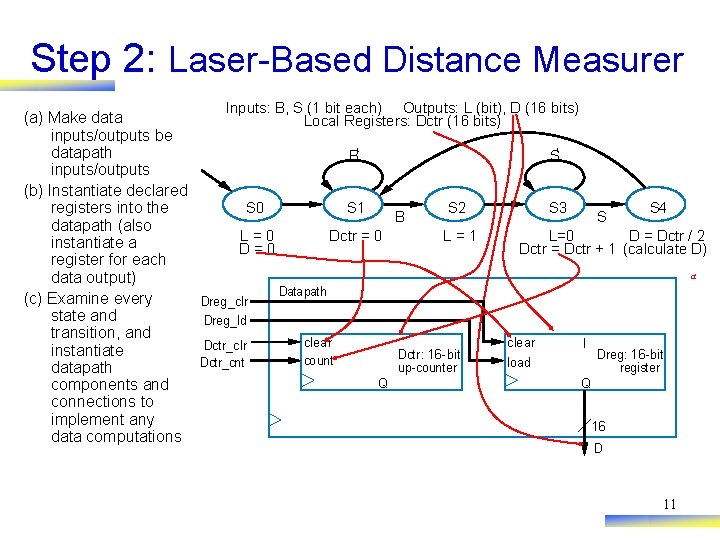
Step 2: Laser-Based Distance Measurer Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) (a) Make data Local Registers: Dctr (16 bits) inputs/outputs be datapath B‘ S‘ inputs/outputs (b) Instantiate declared S 4 S 0 S 1 S 2 S 3 registers into the B S datapath (also L=0 Dctr = 0 L=1 L=0 D = Dctr / 2 instantiate a D=0 Dctr = Dctr + 1 (calculate D) register for each a data output) Datapath (c) Examine every Dreg_clr state and Dreg_ld transition, and clear I Dctr_clr instantiate Dctr: 16 -bit Dreg: 16 -bit count Dctr_cnt load up-counter register datapath Q Q components and connections to implement any 16 data computations D 11

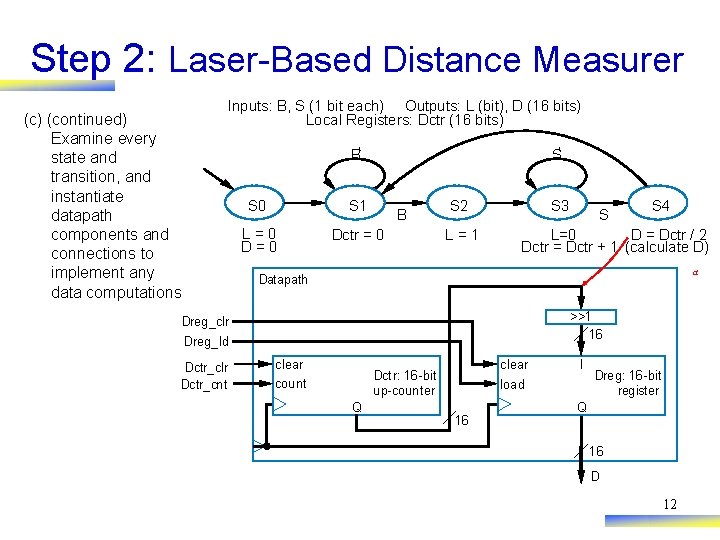
Step 2: Laser-Based Distance Measurer (c) (continued) Examine every state and transition, and instantiate datapath components and connections to implement any data computations Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) Local Registers: Dctr (16 bits) B‘ S‘ S 0 S 1 L=0 Dctr = 0 B S 2 L=1 S 3 S S 4 L=0 D = Dctr / 2 Dctr = Dctr + 1 (calculate D) a Datapath >>1 16 Dreg_clr Dreg_ld Dctr_clr Dctr_cnt clear count clear Dctr: 16 -bit up-counter Q I load 16 Dreg: 16 -bit register Q 16 D 12

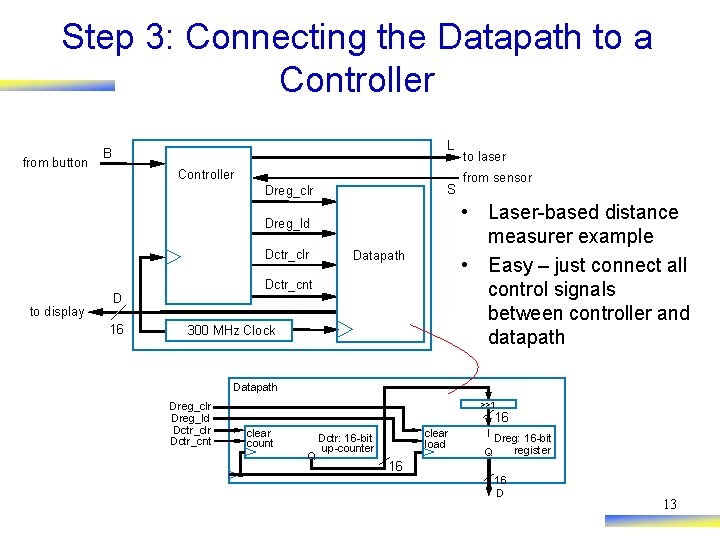
Step 3: Connecting the Datapath to a Controller from button L B Controller S Dreg_clr to display 16 Datapath Dctr_cnt D from sensor • Laser-based distance measurer example • Easy – just connect all control signals between controller and datapath Dreg_ld Dctr_clr to laser 300 MHz Clock Datapath Dreg_clr Dreg_ld Dctr_clr Dctr_cnt >>1 16 clear count Q clear load Dctr: 16 -bit up-counter I Dreg: 16 -bit register Q 16 16 D 13

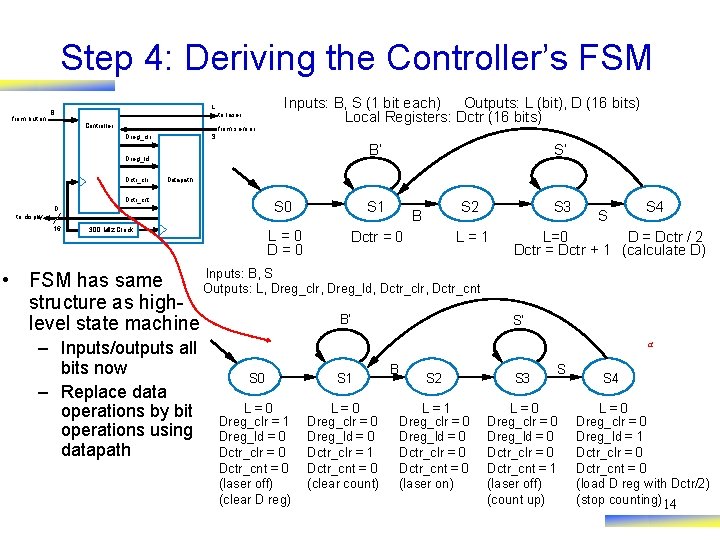
Step 4: Deriving the Controller’s FSM from butt on L B Controller to laser from sensor Inputs: B, S (1 bit each) Outputs: L (bit), D (16 bits) Local Registers: Dctr (16 bits) S Dreg_clr B’ Dreg_ld Dctr_clr Datapath Dctr_cnt D to display 16 S’ 300 MHz Clock S 0 S 1 L=0 Dctr = 0 S 2 B L=1 Inputs: B, S • FSM has same Outputs: L, Dreg_clr, Dreg_ld, Dctr_clr, Dctr_cnt structure as high. B’ level state machine – Inputs/outputs all bits now – Replace data operations by bit operations using datapath S 3 S S 4 L=0 D = Dctr / 2 Dctr = Dctr + 1 (calculate D) S’ a S 0 S 1 L=0 Dreg_clr = 1 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 0 (laser off) (clear D reg) L=0 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 1 Dctr_cnt = 0 (clear count) B S S 2 S 3 L=1 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 0 (laser on) L=0 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 1 (laser off) (count up) S 4 L=0 Dreg_clr = 0 Dreg_ld = 1 Dctr_clr = 0 Dctr_cnt = 0 (load D reg with Dctr/2) (stop counting) 14

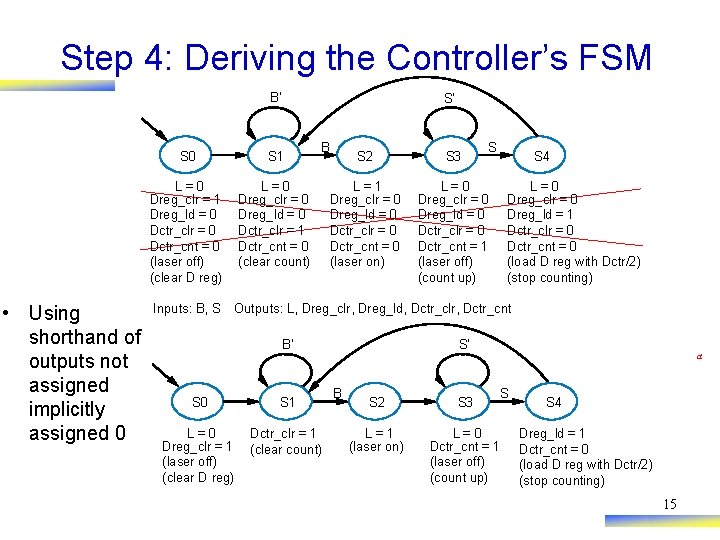
Step 4: Deriving the Controller’s FSM B’ • Using shorthand of outputs not assigned implicitly assigned 0 S’ S 0 S 1 L=0 Dreg_clr = 1 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 0 (laser off) (clear D reg) L=0 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 1 Dctr_cnt = 0 (clear count) Inputs: B, S B S S 2 S 3 L=1 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 0 (laser on) L=0 Dreg_clr = 0 Dreg_ld = 0 Dctr_clr = 0 Dctr_cnt = 1 (laser off) (count up) S 4 L=0 Dreg_clr = 0 Dreg_ld = 1 Dctr_clr = 0 Dctr_cnt = 0 (load D reg with Dctr/2) (stop counting) Outputs: L, Dreg_clr, Dreg_ld, Dctr_clr, Dctr_cnt B’ S 0 S 1 L=0 Dreg_clr = 1 (laser off) (clear D reg) Dctr_clr = 1 (clear count) S’ B a S S 2 S 3 L=1 (laser on) L=0 Dctr_cnt = 1 (laser off) (count up) S 4 Dreg_ld = 1 Dctr_cnt = 0 (load D reg with Dctr/2) (stop counting) 15

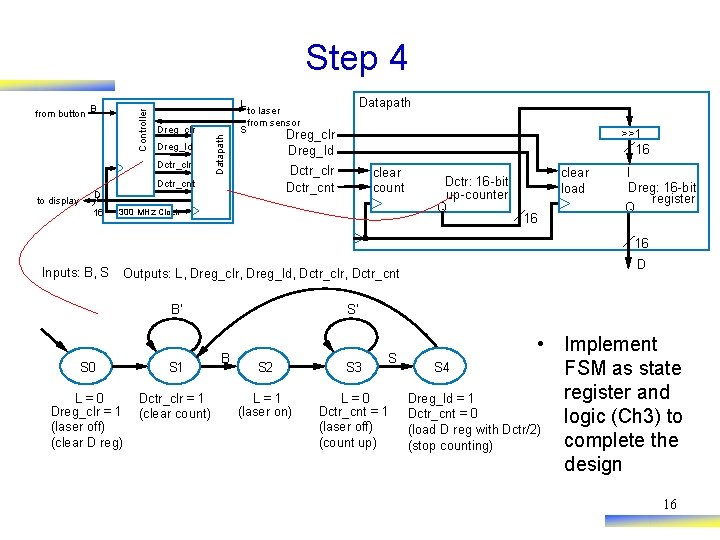
Step 4 L Dreg_clr Dreg_ld Dctr_clr to display S Datapath to laser from sensor >>1 Dreg_clr Dreg_ld 16 Dctr_clr Dctr_cnt D 16 Datapath B Controller from button clear count 300 MHz Clock Dctr: 16 -bit up-counter Q clear load 16 I Dreg: 16 -bit register Q 16 Inputs: B, S Outputs: L, Dreg_clr, Dreg_ld, Dctr_clr, Dctr_cnt B’ S 0 S 1 L=0 Dreg_clr = 1 (laser off) (clear D reg) Dctr_clr = 1 (clear count) D S’ B S S 2 S 3 L=1 (laser on) L=0 Dctr_cnt = 1 (laser off) (count up) • Implement S 4 FSM as state register and Dreg_ld = 1 Dctr_cnt = 0 logic (Ch 3) to (load D reg with Dctr/2) complete the (stop counting) design 16

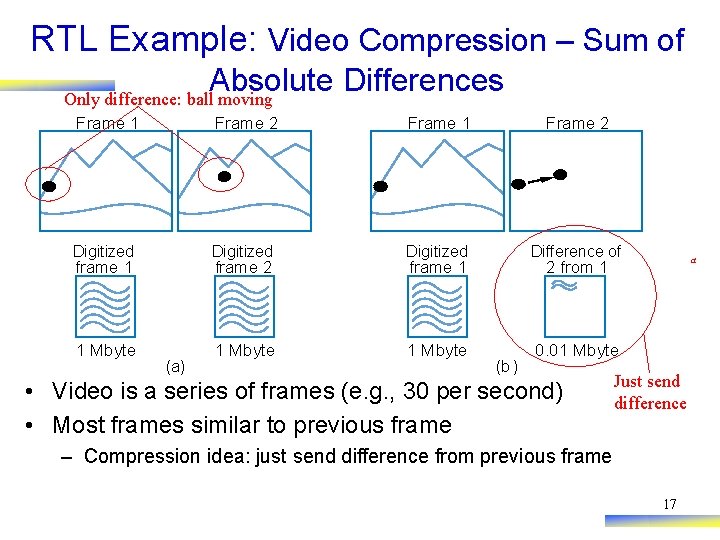
RTL Example: Video Compression – Sum of Absolute Differences Only difference: ball moving Frame 1 Frame 2 Digitized Difference of 1 Mbyte 0. 01 Mbyte frame 1 frame 2 (a) frame 1 a 2 from 1 (b) • Video is a series of frames (e. g. , 30 per second) • Most frames similar to previous frame Just send difference – Compression idea: just send difference from previous frame 17

RTL Example: Video Compression – Sum of compare Frame 1 Absolute Differences Frame 2 Assume each pixel is represented as 1 byte (actually, a color picture might have 3 bytes per pixel, for intensity of red, green, and blue components of pixel) • Need to quickly determine whether two frames are similar enough to just send difference for second frame – Compare corresponding 16 x 16 “blocks” • Treat 16 x 16 block as 256 -byte array – Compute the absolute value of the difference of each array item – Sum those differences – if above a threshold, send complete frame for second frame; if below, can use difference method (using another technique, not described) 18

RTL Example: Video Compression – Sum of Absolute Differences 256 -byte array A 256 -byte array B SAD sad integer go !(i<256) • Want fast sum-of-absolute-differences (SAD) component – When go=1, sums the differences of element pairs in arrays A and B, outputs that sum 19

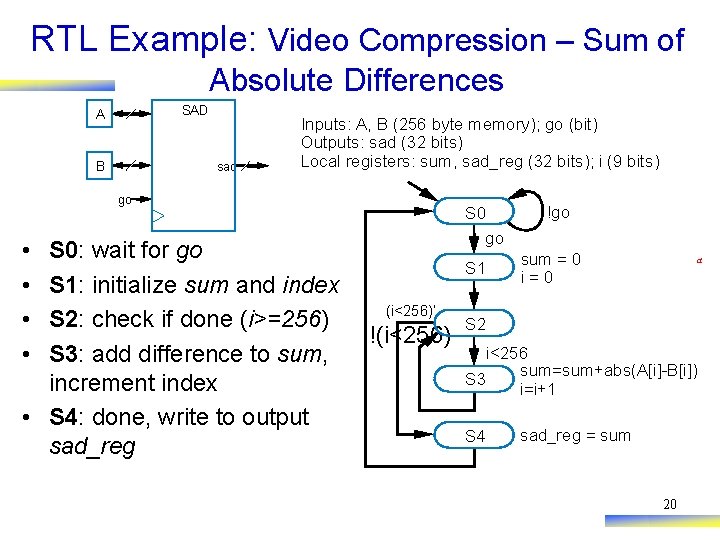
RTL Example: Video Compression – Sum of Absolute Differences SAD A sad B Inputs: A, B (256 byte memory); go (bit) Outputs: sad (32 bits) Local registers: sum, sad_reg (32 bits); i (9 bits) go • • S 0: wait for go S 1: initialize sum and index S 2: check if done (i>=256) S 3: add difference to sum, increment index • S 4: done, write to output sad_reg S 0 go S 1 (i<256)’ !(i<256) !go sum = 0 i=0 a S 2 i<256 sum=sum+abs(A[i]-B[i]) S 3 i=i+1 S 4 sad_reg = sum 20

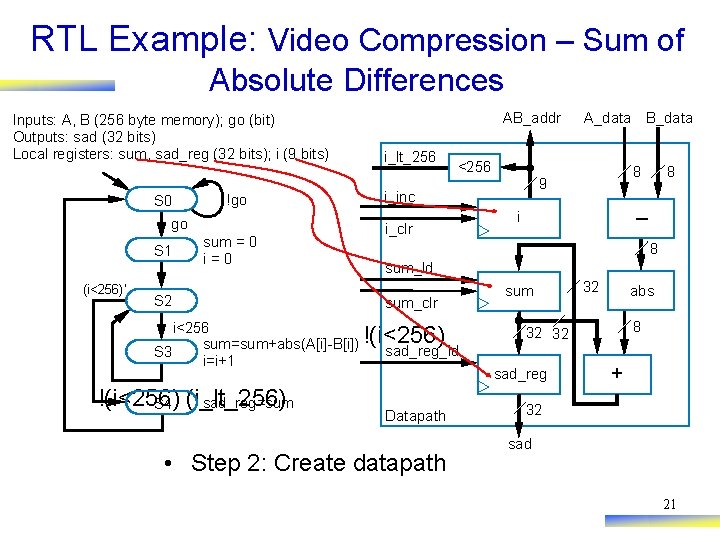
RTL Example: Video Compression – Sum of Absolute Differences Inputs: A, B (256 byte memory); go (bit) Outputs: sad (32 bits) Local registers: sum, sad_reg (32 bits); i (9 bits) S 0 !go go S 1 (i<256)’ sum = 0 i=0 S 2 i<256 sum=sum+abs(A[i]-B[i]) S 3 i=i+1 !(i<256) sad_reg=sum S 4 (i_lt_256) AB_addr i_lt_256 A_data B_data <256 i_inc i_clr 8 9 8 – i 8 sum_ld sum_clr !(i<256) sum 32 abs 8 32 32 sad_reg_ld sad_reg Datapath • Step 2: Create datapath + 32 sad 21

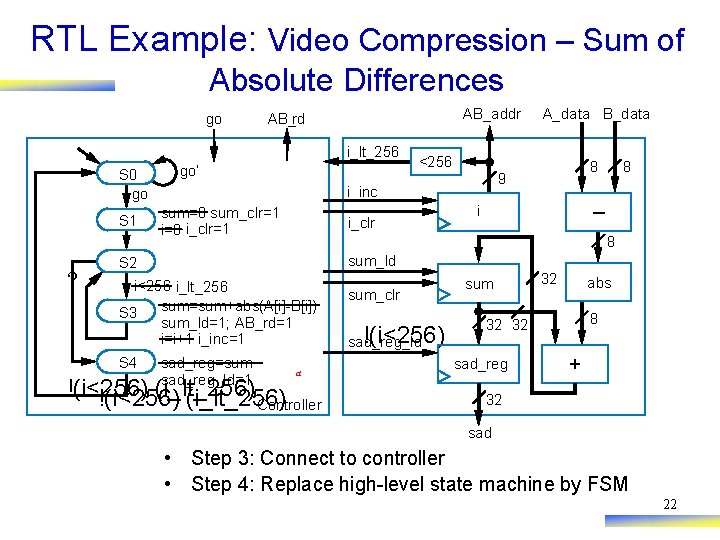
RTL Example: Video Compression – Sum of Absolute Differences go AB_addr AB_rd i_lt_256 S 0 go S 1 ? go’ i_clr 8 9 8 – i 8 sum_ld S 2 i<256 i_lt_256 sum=sum+abs(A[i]-B[i]) S 3 sum_ld=1; AB_rd=1 i=i+1 i_inc=1 S 4 <256 i_inc sum=0 sum_clr=1 i=0 i_clr=1 A_data B_data sad_reg=sum sad_reg_ld=1 a !(i<256) (i_lt_256) Controller sum_clr !(i<256) sad_reg_ld sum 32 abs 8 32 32 sad_reg + 32 sad • Step 3: Connect to controller • Step 4: Replace high-level state machine by FSM 22

RTL Example: Video Compression – Sum of Absolute Differences • Comparing software and custom circuit SAD – Circuit: Two states (S 2 & S 3) for each i, 256 i’s 512 clock cycles (i<256)’ – Software: Loop (for i = 1 to 256), but for each i, must move memory to local registers, subtract, compute absolute value, add to sum, !(i<256) increment i – say about 6 cycles per array item 256*6 = 1536 cycles – !(i<256) Circuit is (i_lt_256) about 3 times (300%) faster S 2 i<256 sum=sum+abs(A[i]-B[i]) S 3 i=i+1 23

Control vs. Data Dominated RTL Design • Designs often categorized as control-dominated or datadominated – Control-dominated design – Controller contains most of the complexity – Data-dominated design – Datapath contains most of the complexity – General, descriptive terms – no hard rule that separates the two types of designs – Laser-based distance measurer – control dominated – SAD circuit – mix of control and data – Now let’s do a data dominated design 24

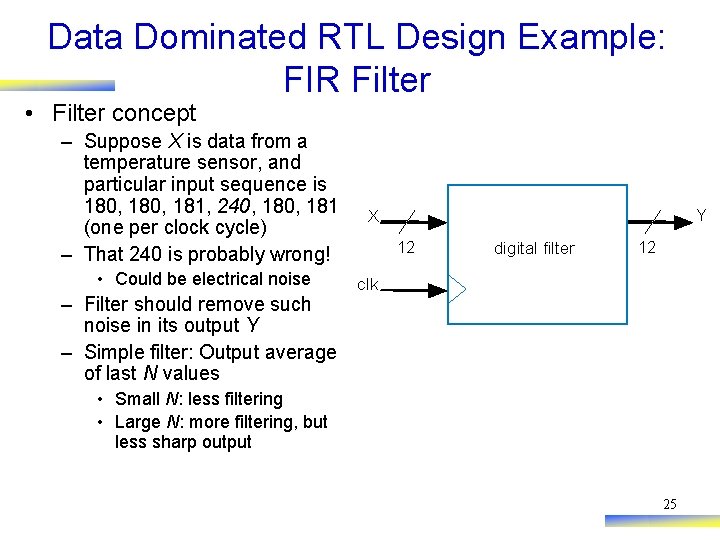
Data Dominated RTL Design Example: FIR Filter • Filter concept – Suppose X is data from a temperature sensor, and particular input sequence is 180, 181, 240, 181 (one per clock cycle) – That 240 is probably wrong! • Could be electrical noise – Filter should remove such noise in its output Y – Simple filter: Output average of last N values Y X 12 digital filter 12 clk • Small N: less filtering • Large N: more filtering, but less sharp output 25

Data Dominated RTL Design Example: FIR Filter • FIR filter – “Finite Impulse Response” – Simply a configurable weighted sum of past input values – y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) • Above known as “ 3 tap” • Tens of taps more common • Very general filter – User sets the constants (c 0, c 1, c 2) to define specific filter Y X 12 digital filter 12 clk y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) – RTL design • Step 1: Create high-level state machine – But there really is none! Data dominated indeed. • Go straight to step 2 26

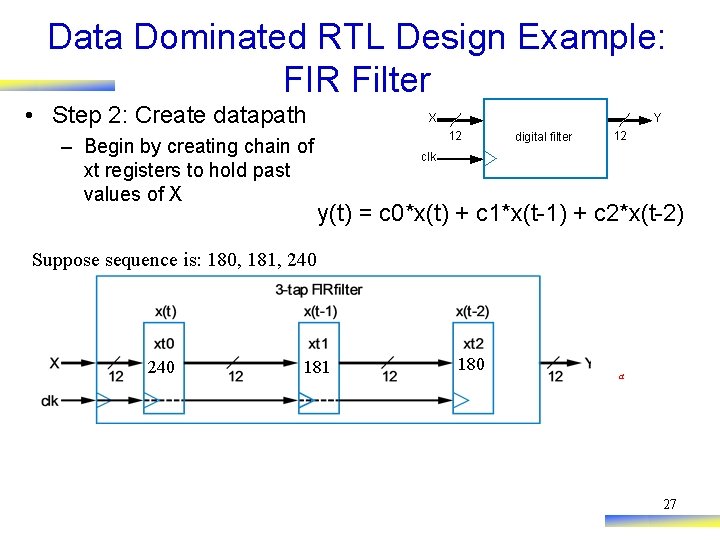
Data Dominated RTL Design Example: FIR Filter • Step 2: Create datapath – Begin by creating chain of xt registers to hold past values of X Y X 12 digital filter 12 clk y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) Suppose sequence is: 180, 181, 240 180 181 180 a 27

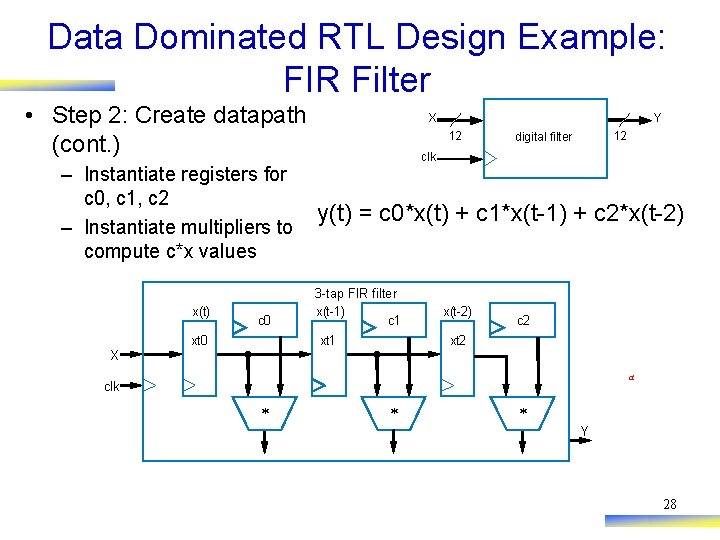
Data Dominated RTL Design Example: FIR Filter • Step 2: Create datapath (cont. ) – Instantiate registers for c 0, c 1, c 2 – Instantiate multipliers to compute c*x values x(t) c 0 xt 0 Y X 12 12 digital filter clk y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) 3 -tap FIR filter x(t-1) c 1 xt 1 x(t-2) c 2 xt 2 X a clk * * * Y 28

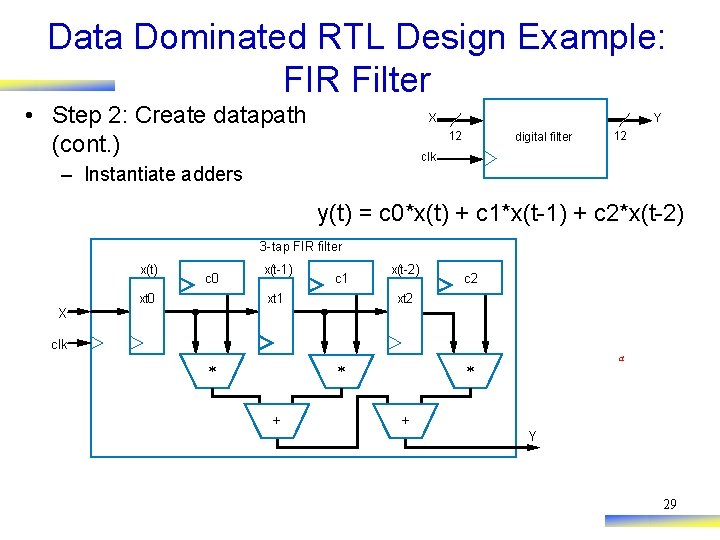
Data Dominated RTL Design Example: FIR Filter • Step 2: Create datapath (cont. ) Y X 12 digital filter 12 clk – Instantiate adders y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) 3 -tap FIR filter x(t) c 0 xt 0 x(t-1) c 1 xt 1 x(t-2) c 2 xt 2 X clk * * + a * + Y 29

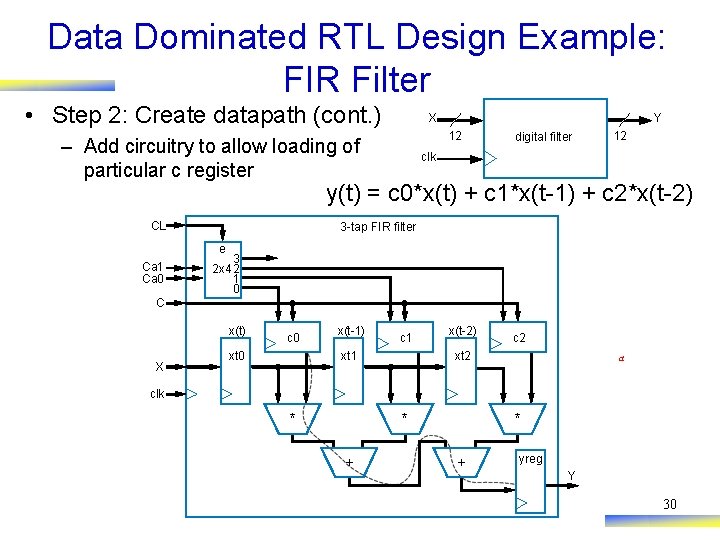
Data Dominated RTL Design Example: FIR Filter • Step 2: Create datapath (cont. ) Y X 12 – Add circuitry to allow loading of particular c register digital filter 12 clk y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) CL 3 -tap FIR filter e Ca 1 Ca 0 3 2 x 4 2 1 0 C x(t) X c 0 xt 0 x(t-1) c 1 xt 1 x(t-2) c 2 xt 2 a clk * * + yreg Y 30

Data Dominated RTL Design Example: FIR Filter • Step 3 & 4: Connect to controller, Create FSM y(t) = c 0*x(t) + c 1*x(t-1) + c 2*x(t-2) – No controller needed – Extreme data-dominated example – (Example of an extreme control-dominated design – an FSM, with no datapath) • Comparing the FIR circuit to a software implementation – Circuit • Assume adder has 2 -gate delay, multiplier has 20 -gate delay • Longest past goes through one multiplier and two adders – 20 + 2 = 24 -gate delay • 100 -tap filter, following design on previous slide, would have about a 34 -gate delay: 1 multiplier and 7 adders on longest path – Software • 100 -tap filter: 100 multiplications, 100 additions. Say 2 instructions per multiplication, 2 per addition. Say 10 -gate delay per instruction. • (100*2 + 100*2)*10 = 4000 gate delays – Circuit is more than 100 times faster (10, 000% faster). 31