Register Allocation via Coloring of Chordal Graphs Fernando

Register Allocation via Coloring of Chordal Graphs Fernando M Q Pereira Jens Palsberg UCLA

95% of the interference graphs produced from Java Methods by the Joe. Q compiler are Chordal. • Java 1. 5 library: 95. 5% (23, 681 methods). • Public ML graphs: 94. 1% (27, 921 IG’s). – Not considering pre-colored registers. • But, what is a chordal graph?

Why is this good news? • Many problems that are NP-complete for general graphs are linear time for chordal graphs. Ex. graph coloring. • Simpler register allocation algorithms, but still competitive!

Register Allocation is Complicated… • Iterated Register Coalescing [George and Appel 96] build actual spill simplify select coalesce freeze potential spill

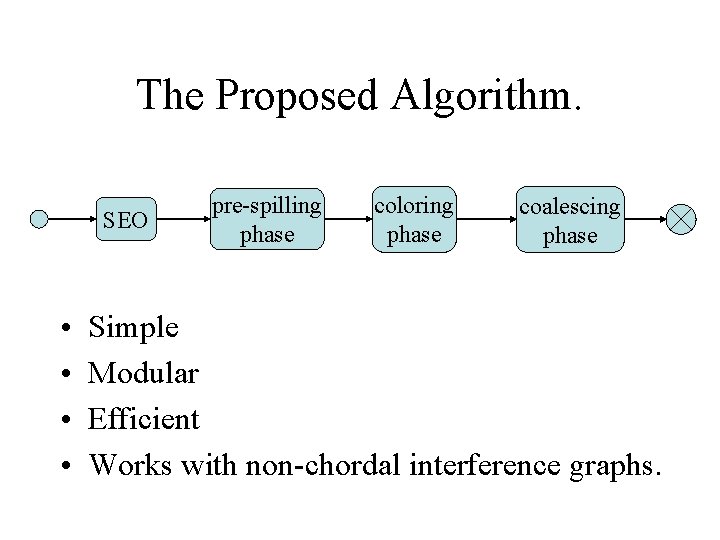
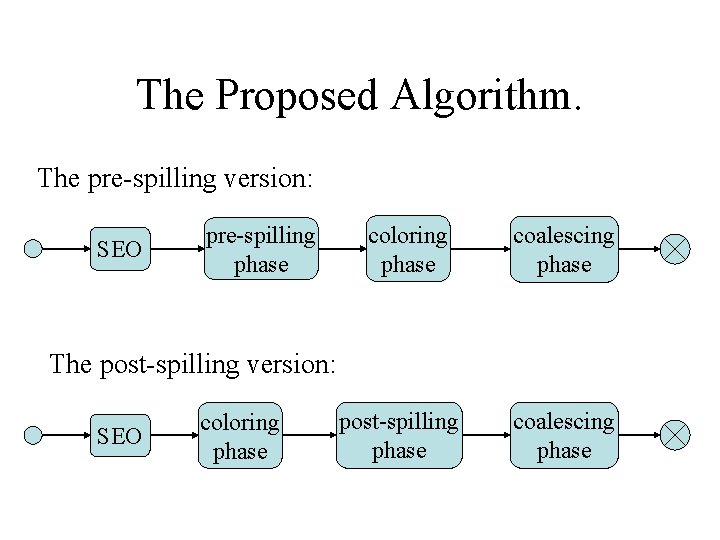
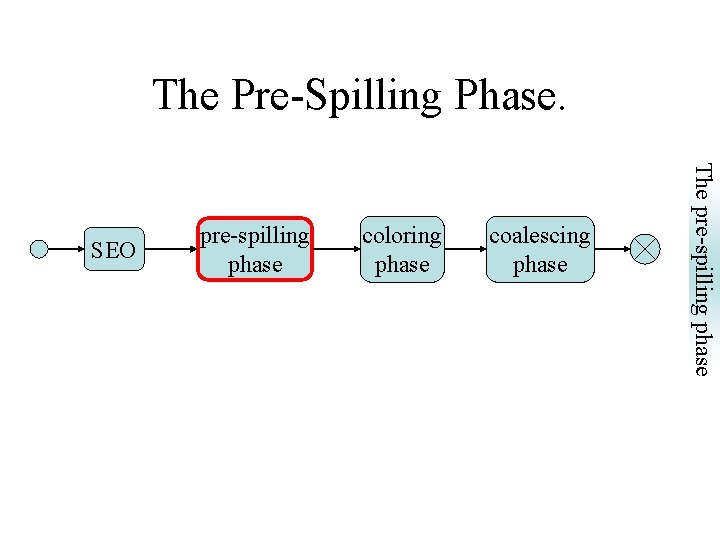
The Proposed Algorithm. SEO • • pre-spilling phase coloring phase coalescing phase Simple Modular Efficient Works with non-chordal interference graphs.

Some terminology: – Induced subgraphs: H = G[VH] A B A C D B C E D – Induced cycles: H is a cycle. A B E D E C D – Clique: H is a complete graph. A B A C D C E D

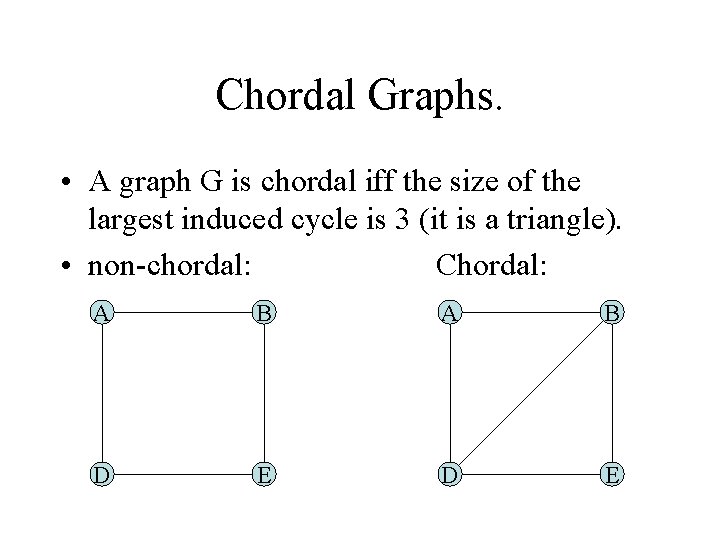
Chordal Graphs. • A graph G is chordal iff the size of the largest induced cycle is 3 (it is a triangle). • non-chordal: Chordal: A B D E

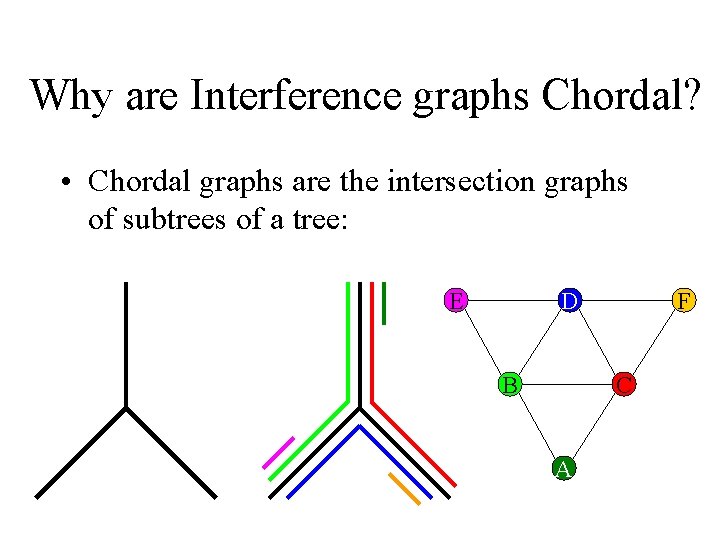
Why are Interference graphs Chordal? • Chordal graphs are the intersection graphs of subtrees of a tree: E D B F C A

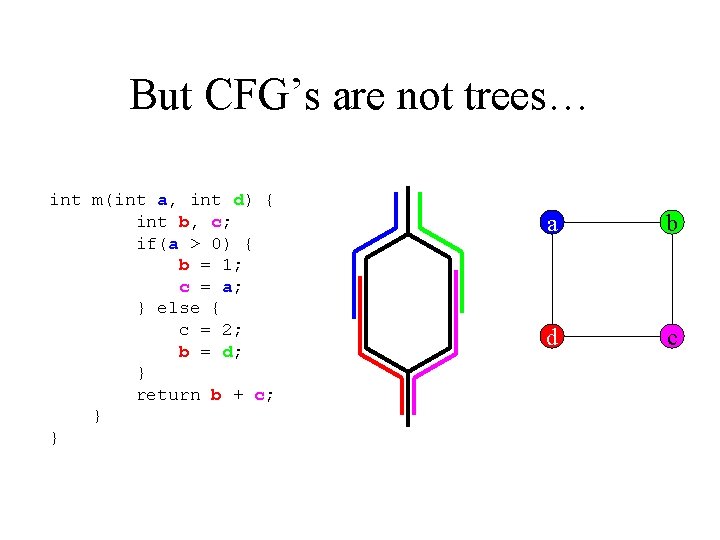
But CFG’s are not trees… int m(int a, int d) { int b, c; if(a > 0) { b = 1; c = a; } else { c = 2; b = d; } return b + c; } } a b d c

Interference graphs of programs in SSA form are chordal. • Independently proved by Brisk[2005], Hack[2005], Bouchez[2005]. • Intuition: – The chordal graphs are the intersection graphs of subtrees of a tree. – Live ranges in SSA are subtrees of the dominance tree.

Why only 95% of chordal graphs? • Executable code is not in SSA form. • SSA elimination. – Phi-functions are abstract constructions. – In executable code, phi functions are replaced by copy instructions. • We call programs after SSA elimination Post. SSA programs. • Some Post-SSA programs are non-chordal : (

The Proposed Algorithm. The pre-spilling version: SEO pre-spilling phase coloring phase coalescing phase The post-spilling version: SEO coloring phase post-spilling phase coalescing phase

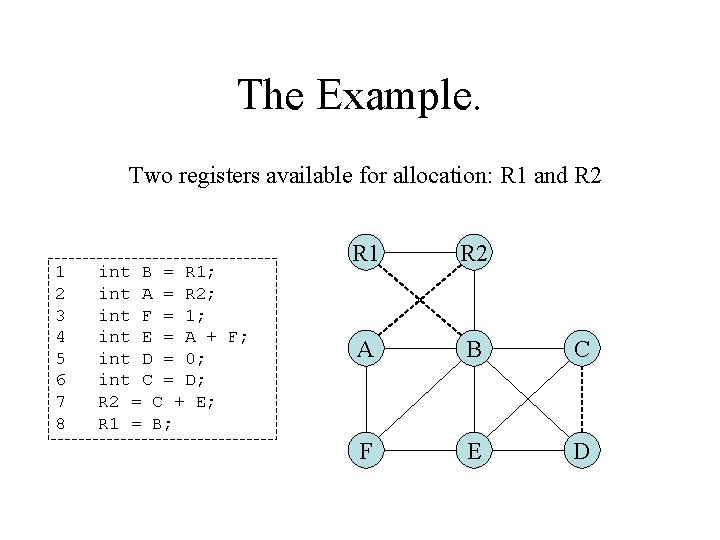
The Example. Two registers available for allocation: R 1 and R 2 1 2 3 4 5 6 7 8 int B = R 1; int A = R 2; int F = 1; int E = A + F; int D = 0; int C = D; R 2 = C + E; R 1 = B; R 1 R 2 A B C F E D

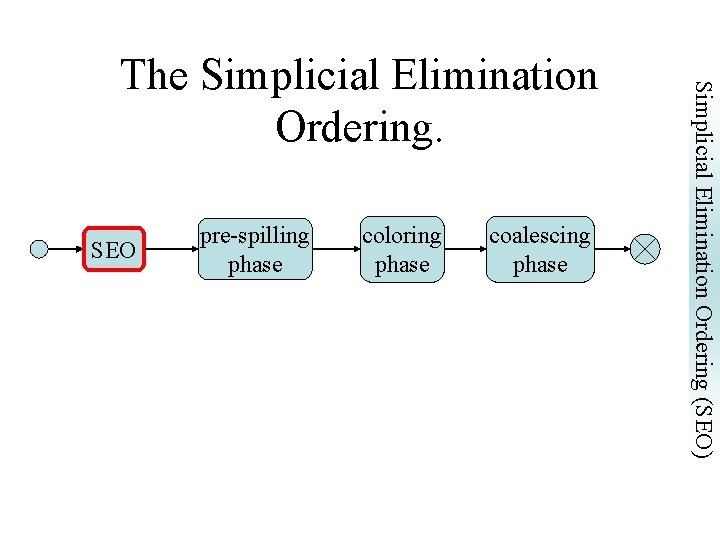
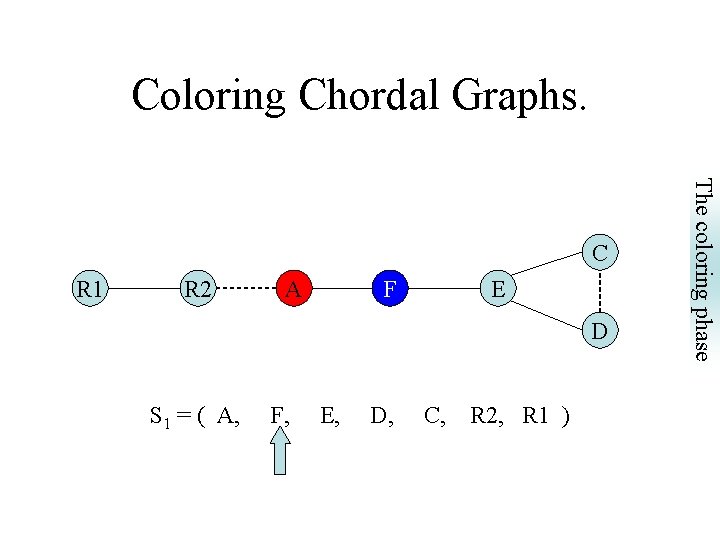
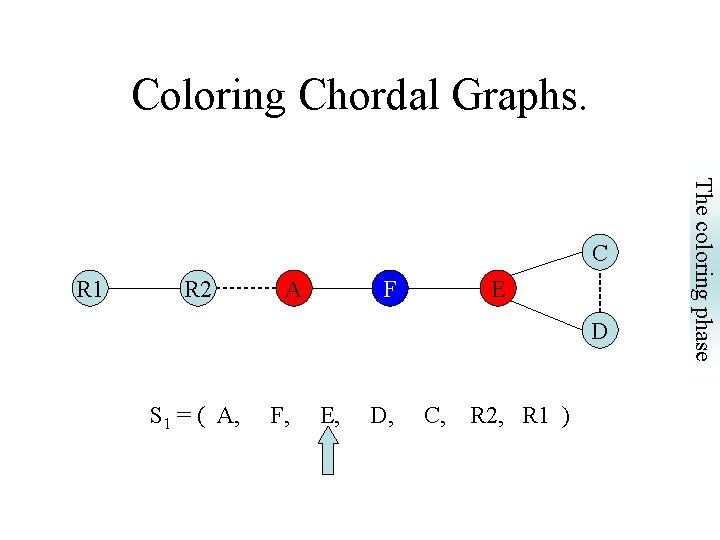
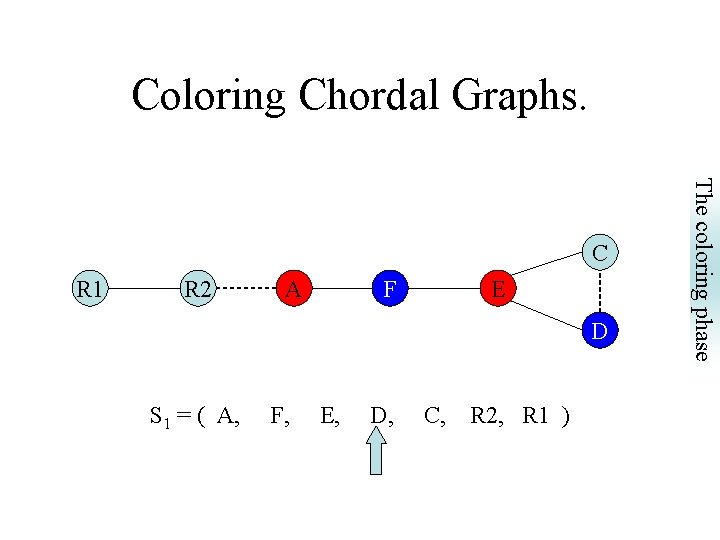
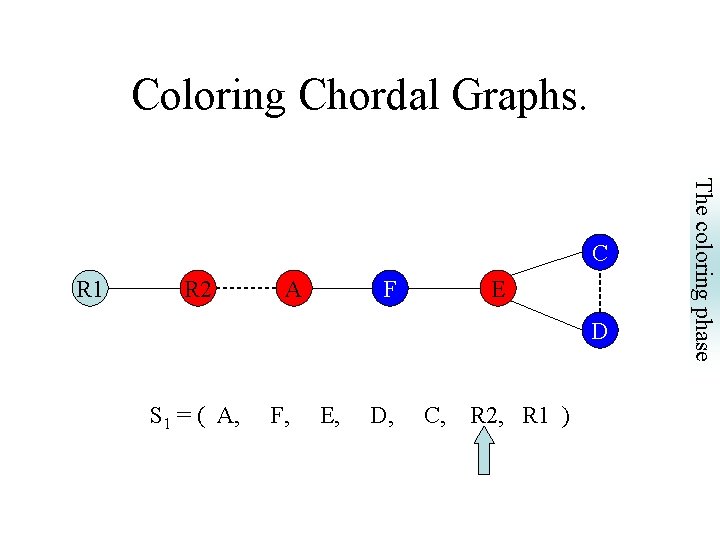
SEO pre-spilling phase coloring phase coalescing phase Simplicial Elimination Ordering (SEO) The Simplicial Elimination Ordering.

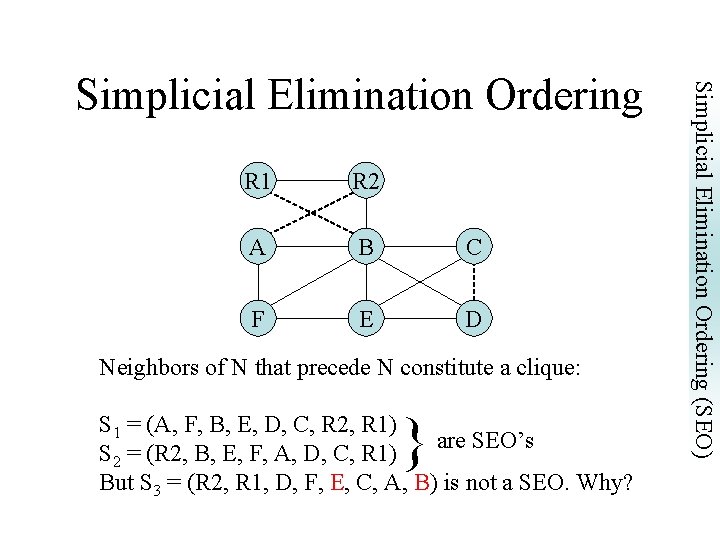
R 1 R 2 A B C F E D Neighbors of N that precede N constitute a clique: } S 1 = (A, F, B, E, D, C, R 2, R 1) are SEO’s S 2 = (R 2, B, E, F, A, D, C, R 1) But S 3 = (R 2, R 1, D, F, E, C, A, B) is not a SEO. Why? Simplicial Elimination Ordering (SEO) Simplicial Elimination Ordering

• A graph G = (V, E) is chordal if, and only if, it has a simplicial elimination ordering [Dirac 61]. • There exist O(|V| + |E|) algorithms to find a simplicial elimination ordering: – Maximum Cardinality Search, – Lexicographical Breadth First Search. Simplicial Elimination Ordering (SEO) A third definition of chordal graph.

The Pre-Spilling Phase. coloring phase coalescing phase The pre-spilling phase SEO pre-spilling phase

The Pre-Spilling Phase – For each register r: • n = number of big cliques that contain r. • f = frequency of use. • s = size of r’s live range. – Spill factor = n * s / f The pre-spilling phase • Chromatic number = size of largest clique. 1 - List all the maximal cliques in the graph. 2 - Remove nodes until all maximal cliques have K or less nodes. 2. 1 - Which registers to remove?

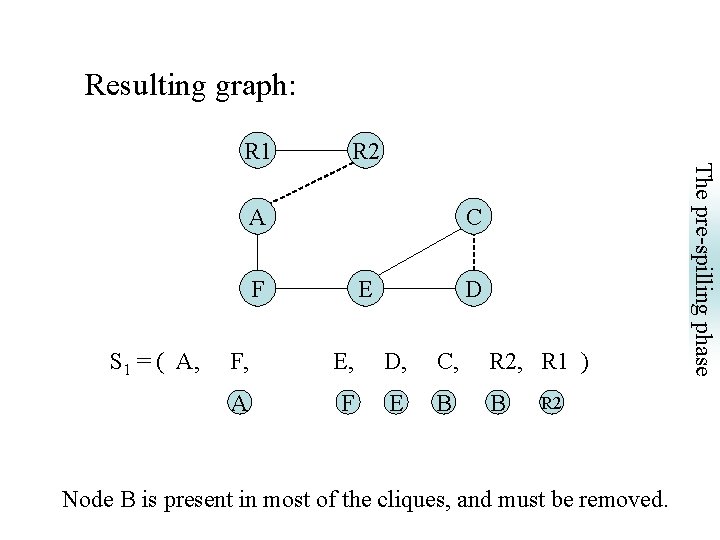
Only look into cliques greater than K = 2. R 2 A B C F E D F, B, E, D, C, R 2, R 1 ) A A B B F F E R 2 Node B is present in most of the cliques, and must be removed. The pre-spilling phase S 1 = ( A, R 1

Resulting graph: R 2 A C F S 1 = ( A, E D F, E, D, C, R 2, R 1 ) A F E B B R 2 Node B is present in most of the cliques, and must be removed. The pre-spilling phase R 1

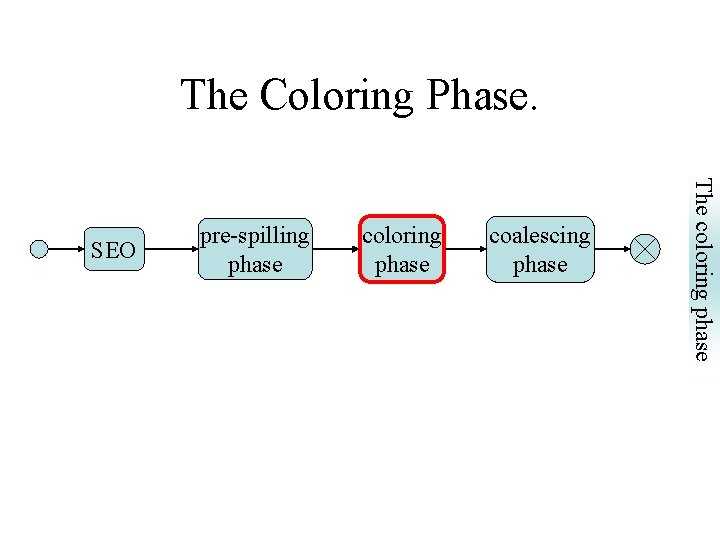
The Coloring Phase. coloring phase coalescing phase The coloring phase SEO pre-spilling phase

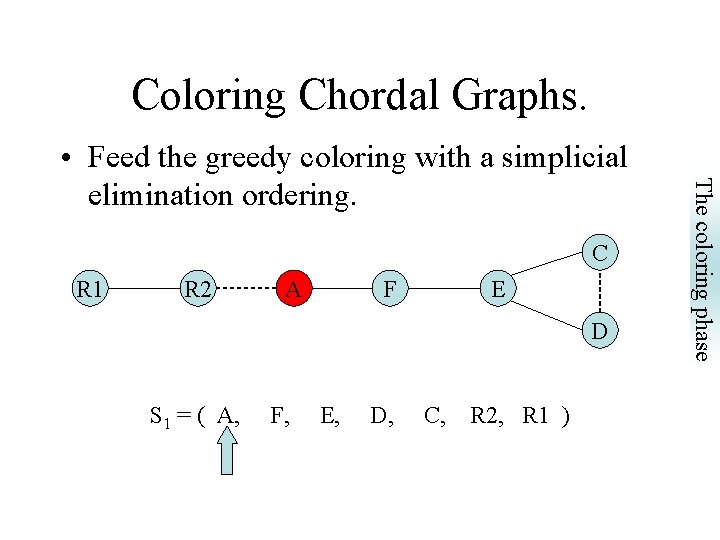
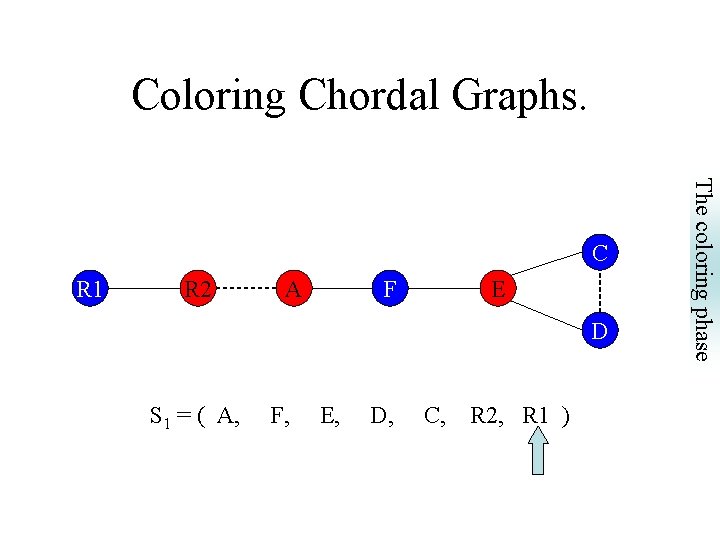
Coloring Chordal Graphs. C R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase • Feed the greedy coloring with a simplicial elimination ordering.

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Coloring Chordal Graphs. R 1 R 2 A F E D S 1 = ( A, F, E, D, C, R 2, R 1 ) The coloring phase C

Register Coalescing. pre-spilling phase coloring phase coalescing phase The coalescing phase SEO

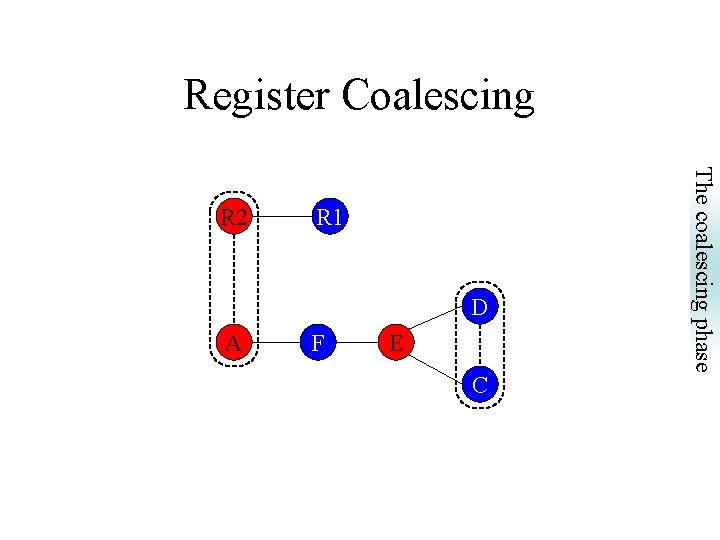
Register Coalescing – Why not before graph coloring? Algorithm: Register Coalescing Input: (G, color(G)) Output: (G, color’(G)) begin for every non-interfering move instruction (x : = y) do let color(x) = color(y) = unused color(N(x) U N(y)); end The coalescing phase • Greedy coalescing after register allocation.

Register Coalescing R 1 D A F E C The coalescing phase R 2

Register Coalescing R 1 D A F E C The coalescing phase R 2

The Post-Spilling Phase. post-spilling phase coalescing phase • Remove nodes assigned same color. E. g: – Remove least used color. – Remove greatest color. • Faster implementation, but generates worse code. The Post-Spilling Phase SEO coloring phase

What about a Non-Chordal Graph? • Coloring is no longer optimal. • The number of colors will be between the optimal, and twice the optimal for almost every possible graph [Bollobas 1988].

Benchmark • The Java 1. 5 standard libraries. – 23, 681 methods. • Algorithms implemented in the Joe. Q framework. • Two test cases: – Code without any transformation: 90% chordal. – Programs in Post-SSA form: 95% chordal.

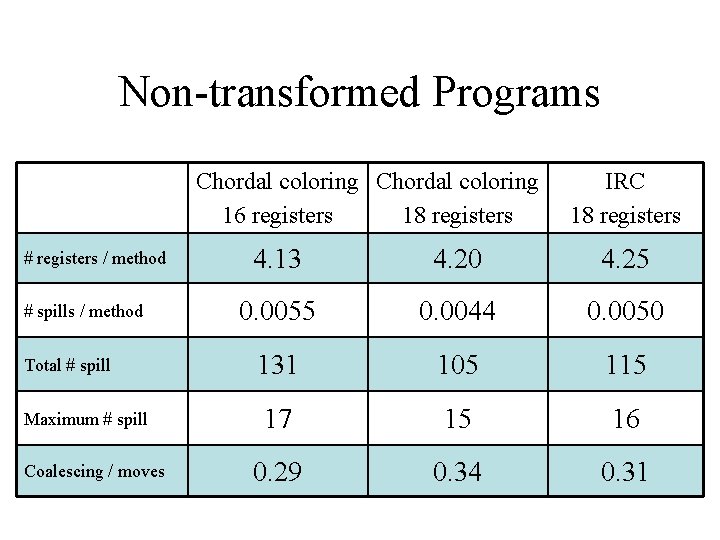
Non-transformed Programs Chordal coloring 16 registers 18 registers # registers / method # spills / method Total # spill Maximum # spill Coalescing / moves IRC 18 registers 4. 13 4. 20 4. 25 0. 0055 0. 0044 0. 0050 131 105 115 17 15 16 0. 29 0. 34 0. 31

Post-SSA Programs Chordal coloring 16 registers 18 registers # registers / method # spills / method Total # spill Maximum # spill Coalescing / moves IRC 18 registers 4. 12 4. 13 4. 17 0. 0053 0. 0040 0. 0049 125 94 118 16 17 27 0. 68 0. 72 0. 70

Methods in Java 1. 5 • • 23, 681 methods; 22, 544 chordal methods. 85% methods could be colored with 6 regs. 99. 8% could be colored with 16 regs. 28 methods demanded more than 16 regs.

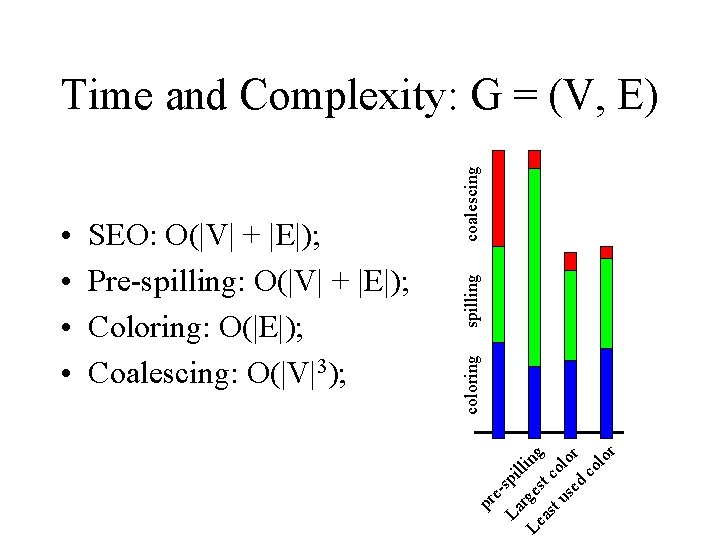
spilling coloring SEO: O(|V| + |E|); Pre-spilling: O(|V| + |E|); Coloring: O(|E|); Coalescing: O(|V|3); pr e. La spi l Le rges ling as t c t u ol se or d co lo r • • coalescing Time and Complexity: G = (V, E)

Related Work. • All the 27, 921 public ML interference graphs are 1 -perfect [Andersson 2003]. – Structured programs have 1 -perfect IG? • Polynomial register allocation [Brisk 2005], [Hack 2005]. – SSA-Interference graphs are chordal.

Conclusions • Many interference graphs of structured programs are chordal; • New algorithm: – Modular; – Efficient; – Competitive; • We have an extended version of the algorithm implemented on top of GCC: – http: //compilers. cs. ucla. edu/fernando/projects/

Are Java Interference Graphs 1 -Perfect? • 1 -Perfect graph: minimum coloring equals largest clique. – It is different of perfect graphs. • All the 27, 921 IG of the ML compiler compiling itself are 1 -perfect [Andersson, 2003]. – Not considering pre-colored registers: 94. 5% of chordal graphs.

SSA and Post-SSA Graphs. • SSA interference graphs: – Chordal – Perfect – 1 -Perfect • Post SSA graphs: – If phi functions are replaced by copy instructions, than register allocation is NPcomplete.

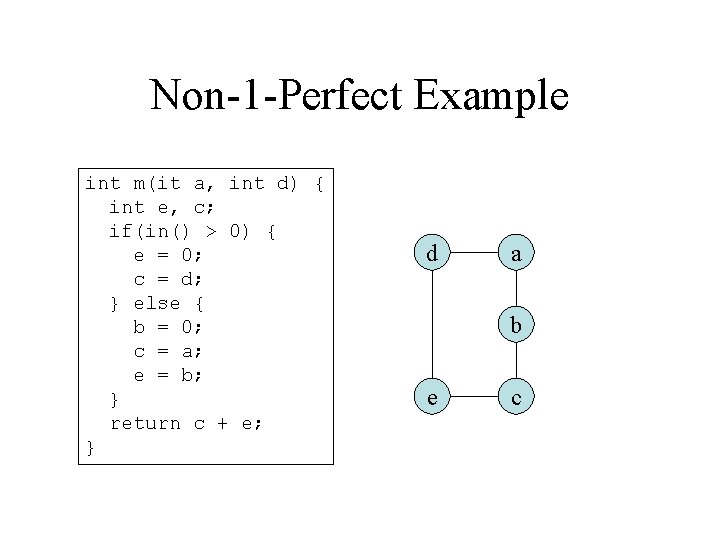
Non-1 -Perfect Example int m(it a, int d) { int e, c; if(in() > 0) { e = 0; c = d; } else { b = 0; c = a; e = b; } return c + e; } d a b e c

The Post SSA Interference Graph. x e 2 = 0; c 2 = d; e = e 2; c = c 2; b = 0; c 1 = d; e 1 = b; c = c 1; e = e 1; return c + e; d a e 2 b c 2 c 1 e e 1 c

References • [Andersson 2003] Christian Andersson, Register Allocation by Optimal Graph Coloring, 12 th Conference on Compiler Construction • [Brisk 2005] Philip Brisk and Foad Dabiri and Jamie Macbeth and Majid Sarrafzadeh, Polynomial-Time Graph Coloring Register Allocation, 14 th International Workshop on Logic and Synthesis • [Hack 2005] Sebastian Hack and Daniel Grund and Gerhard Goos, Towards Register Allocation for Programs in SSA-form.