Refractive Distortions to HBT A Classical View Scott

Refractive Distortions to HBT A Classical View Scott Pratt Michigan State University

OUTLINE • Theory background • Classical description of refractive distortion • Examples • Classical vs. Quantum Cramer et al. , Miller, PRL 94, 102302 (05), Miller and Cramer, nucl-th/0507004 H. W. Barz, PRC 59, 2214 (99); PRC 53, 2536 (96) Scott Pratt Michigan State University

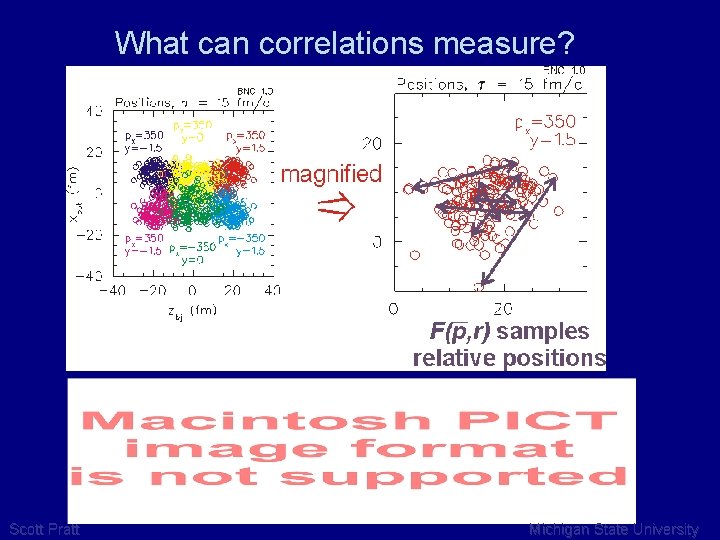
What can correlations measure? Scott Pratt Michigan State University

What is puzzling about HBT • Several simple models work • Blast wave parameters: R=13 fm, =10 fm/c, v=0. 7 c • Surface grows 7 fm in 10 fm/c • What about acceleration? • Reducing Rside or increasing would help Scott Pratt Michigan State University

Adding Mean Field Classical Method: • Calculate trajectories • Weight with 1 + cos(pa-pb)·(xa-xb) Quantum Method: • Sample ‘last-collision’ points • Weight with | (pa, xa)|2| (pb, xb)|2 +� (pa, xa) (pb, xa)· (pa, xb) (pb, xb) Outgoing wave functions Scott Pratt Michigan State University

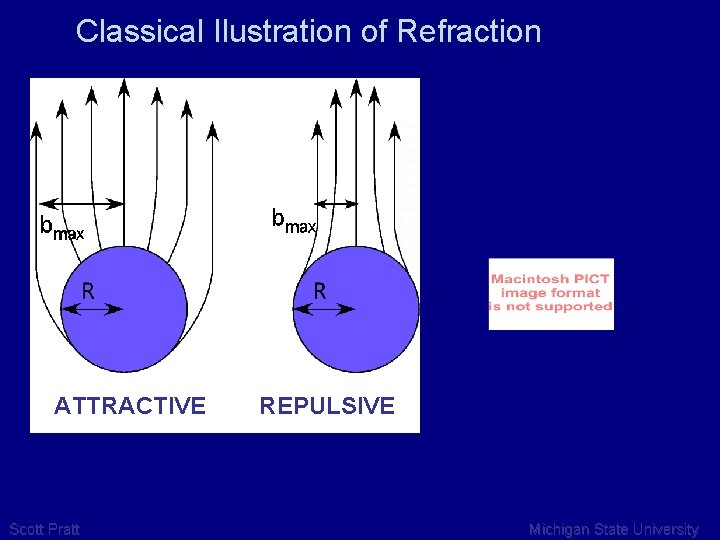
Classical Ilustration of Refraction ATTRACTIVE Scott Pratt REPULSIVE Michigan State University

Louisville Theorem and Refraction • Escaping attractive mean field lowers (contracts) p • Contraction of p space -> expansion of x space Scott Pratt Michigan State University

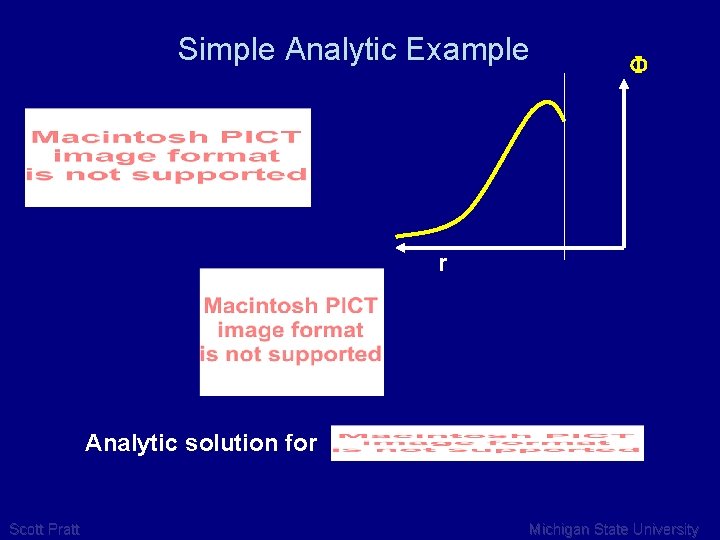
Simple Analytic Example F r Analytic solution for Scott Pratt Michigan State University

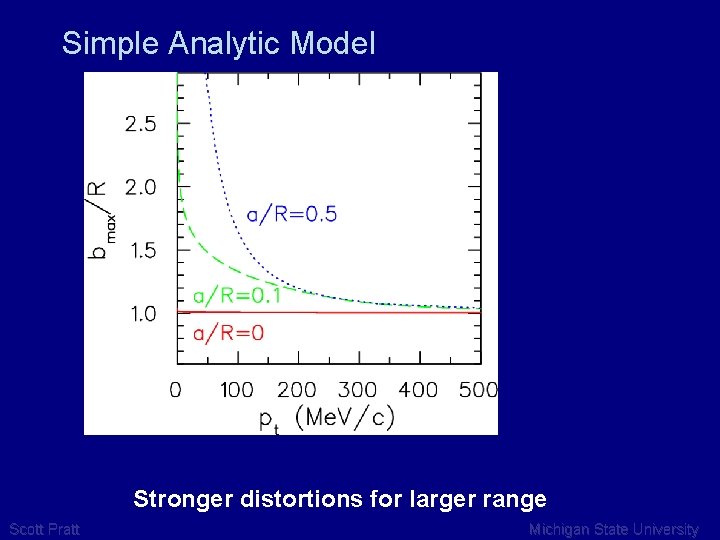
Simple Analytic Model Stronger distortions for larger range Scott Pratt Michigan State University

Simple Model with Collective Flow • • • Classical trajectories begin at R Thermal: T=120, y. M=0. 8 Longitudinal boost invariance Let mean field ~ exp{-(r-R)/a} R moves outward with rapidity ( =9 fm/c, R=9 fm, y. B = 0. 4) ( =12 fm/c, R=12 fm, y. B = 0) ( =15 fm/c, R=9 fm, y. B = -0. 4) • Surface consumes returning trajectories Scott Pratt Michigan State University

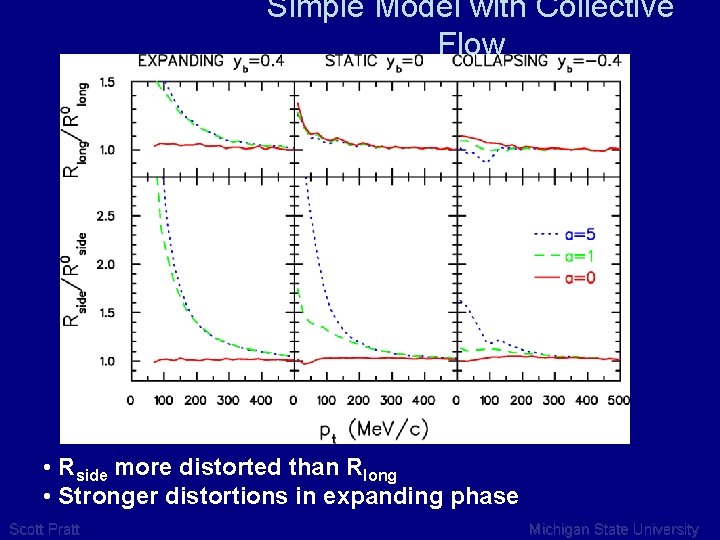
Simple Model with Collective Flow • Rside more distorted than Rlong • Stronger distortions in expanding phase Scott Pratt Michigan State University

Quantum vs. Classical r 0 Scott Pratt Michigan State University

Quantum Classical Scott Pratt Michigan State University

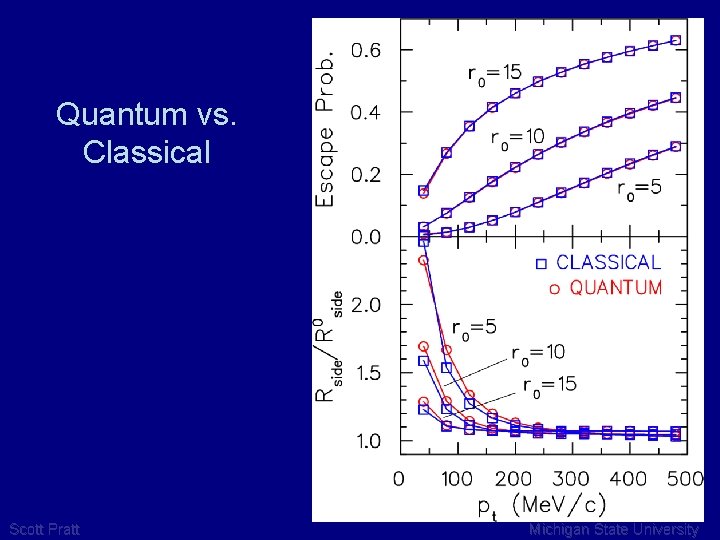
Quantum vs. Classical Scott Pratt Michigan State University

Quantum vs. Classical: Eikonal Phases Kapusta and Li, www. ar. Xiv. org: 0505075 C. Y. Wong, J. Phys G 30, S 1053 (04) [ar. Xiv: hep-ph/0403025 M. Chu et al. , PRC 50, 3079 (94) Interference phase: Use v=d. E/dp & assume pa-pb is small: = Classical asymptotic separation time delay Scott Pratt Michigan State University

Summary • • Refraction can be important Attractive forces help interpretation of Rside Any attractive interaction should help (pisobar…) Classical treatments (Boltzmann) work Scott Pratt Michigan State University