Refraction of light Transition from air to water

Refraction of light Transition from air to water In dense media such as water or glass, light travels slower than in thin media such as air or vacuum. This causes the phenomenon of refraction, which includes the phenomenon of the “broken stick”. The velocity (c) of light in vacuum is 300. 000 km/second, the highest speed possible in our universe. If the velocity of light in a medium is v, then the “refractive index” (n) of that medium is given by: n= c v The refractive idex of matter thus is always greater than 1, for example: Air: n = 1. 0003 Water: n = 1. 33 Glass: n = 1. 52 The refractive index of matter bears relevance to the functionality of security features, such as pearl luster ink, optically variable ink and transparent overlays.

Refraction and reflection of light Transition from “thin” to “dense” matter air water i r Refraction also makes a light beam “break” when it transits from a thin to a dense medium under an angle with the interface between both media. Here a laser beam enters a vessel of water under an angle i to become refracted under an angle r. The laser beam has been visualized by blowing smoke in its path in air and by adding some milk to the water. Willebrord Snel in 1621 discovered the law of refraction, which formulated the relation between the refractive indices of both media n 1 (e. g. of air) and n 2 (e. g. of water) and the angle of entrance i and refraction r: n 1 sin ( i ) = n 2 sin ( r )

Refraction and reflection of light Transition from “thin” to “dense” matter air water i r The phenomenon is sometimes compared to the change of direction that a marching column of soldiers would undergo when it transits from a paved street to loose sand under an angle with the interface between both media: paved street and sand. The soldier that first enters the sand, is slowed down while the soldier next to him still proceeds faster on the paved street. The result is illustrated in the next slide.

Refraction and reflection of light Transition from “thin” to “dense” matter air water n = velocity 1 velocity 2 paved street: fast loose sand: slow Analogy of the marching column of soldiers

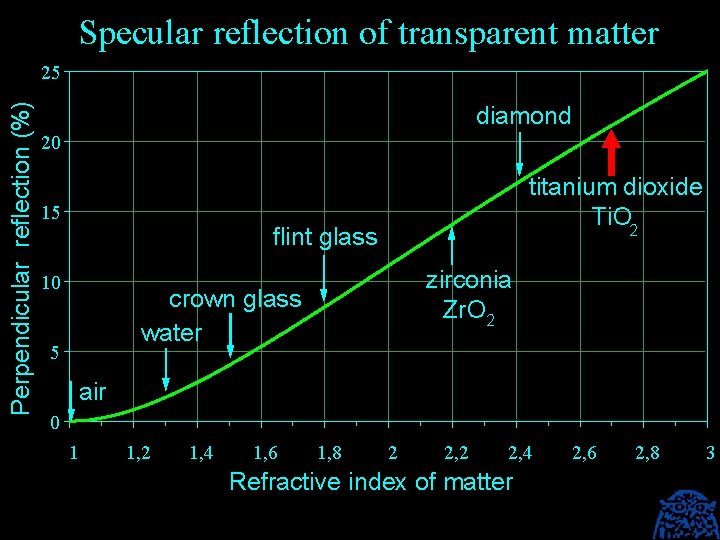
Reflection and refractive index (n) reflection low n = low water n = 1, 33 magnesium fluoride n = 1, 38 reflection high n = high diamond n = 2, 3 titanium dioxide n = 2, 7 The higher the refractive index, the stronger the reflection and the refraction.

Specular reflection of transparent matter Perpendicular reflection (%). 25 diamond 20 15 titanium dioxide Ti. O 2 flint glass 10 zirconia Zr. O 2 crown glass water 5 air 0 1 1, 2 1, 4 1, 6 1, 8 2 2, 4 Refractive index of matter 2, 6 2, 8 3

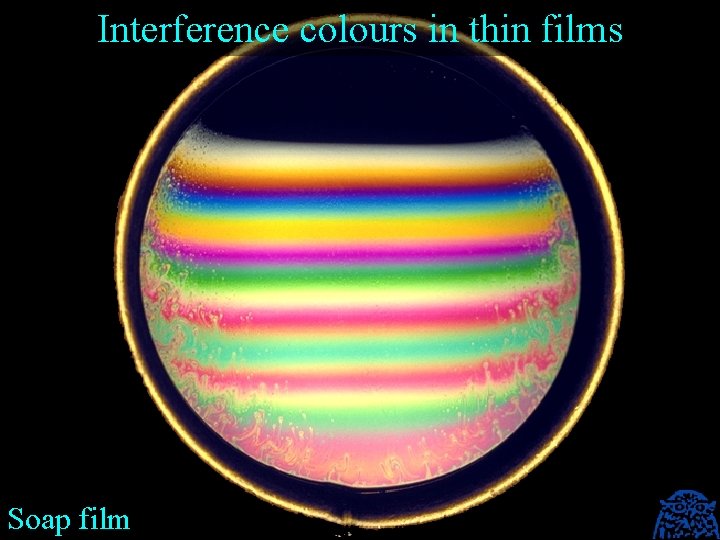
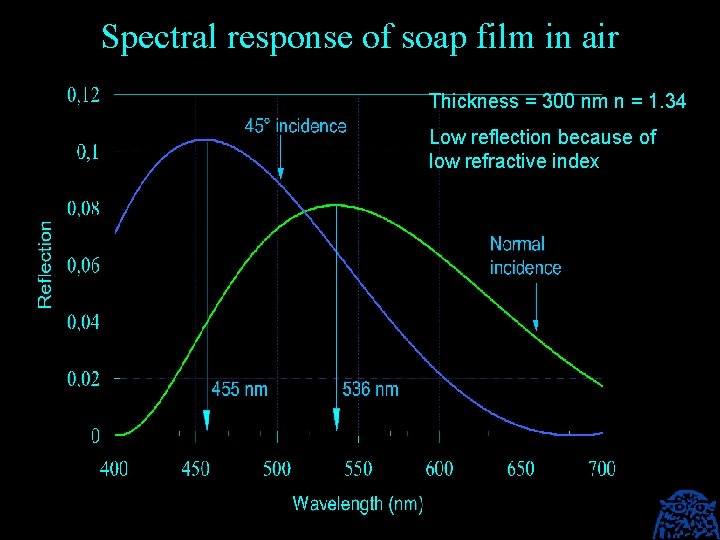
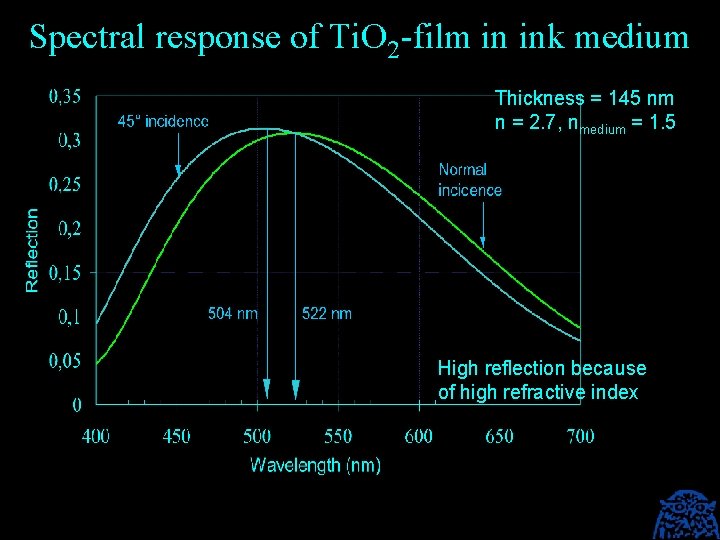
Colour shift and refractive index of single thin interference films The next slides show that thin interference films with a low refractive index, such as a soap film, display a considerable colour shift with the angle of observation. However, because of that low refractive index, their reflection is low. Interference Security Image Structures (ISIS) must have a sufficient reflection and therefore single thin film devices must be based on a high refractive index material. Titanium dioxide (n = 2. 7) is the basis of pearl luster ink. Pearl luster inks have a significant reflection, but, because of their high refractive index, their color shift is negligible. Pearl luster ink is an interference based ink, but calling it iridescent is highly overdone.

Interference colours in thin films Soap film

Interference colours in thin films Newton rings in an air film between two glasses Newton rings in an oil film on a wet road

Spectral response of soap film in air Thickness = 300 nm n = 1. 34 Low reflection because of low refractive index

Pearl luster ink structure Ti. O 2 n = 2, 7 Substrate: mica flakes Ti. O 2 n = 2, 7 Medium: transparent ink

Spectral response of Ti. O 2 -film in ink medium Thickness = 145 nm n = 2. 7, nmedium = 1. 5 High reflection because of high refractive index

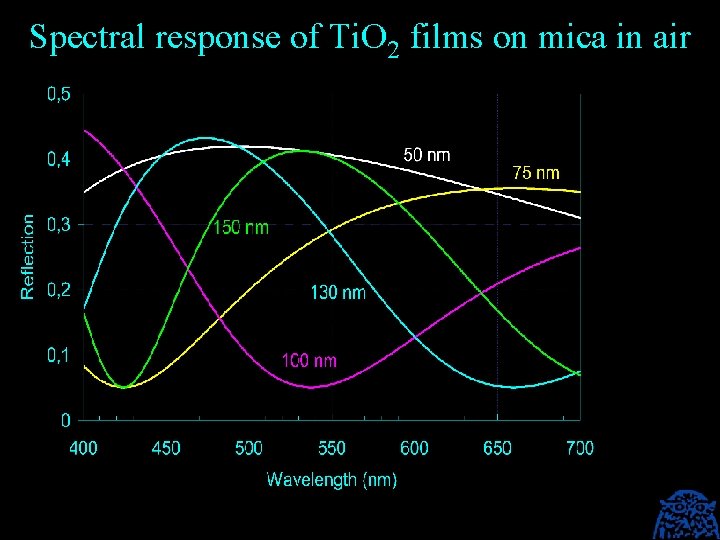
Spectral response of Ti. O 2 films on mica in air

Pearl luster ink on 5, 10 and 20 euro notes

Pearl luster ink on Swiss notes Diffuse reflection (outside the gloss) Reflection (in the gloss)

Pearl lustre ink in transparent window Papua New Guinea 100 kina note with G-switch® feature. The feature shifts between purple in glossy reflection and green against a light background, but displays no appreciable color shift with angle of reflection. No polarization effects are present. This is typical of pearl lustre ink. Black background W purple -purple White printed background

Microphotos of pearl lustre ink transmission 1 div = 10 µm reflection 1 div = 10 µm

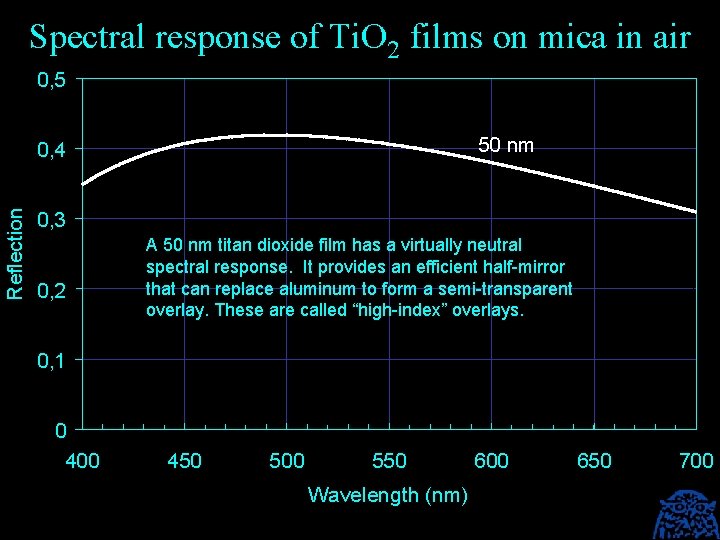
Spectral response of Ti. O 2 films on mica in air 0, 5 50 nm Reflection 0, 4 0, 3 0, 2 A 50 nm titan dioxide film has a virtually neutral spectral response. It provides an efficient half-mirror that can replace aluminum to form a semi-transparent overlay. These are called “high-index” overlays. 0, 1 0 400 450 500 550 Wavelength (nm) 600 650 700

Transparent (high-index) overlay film Replace aluminium by a high refractive index substance such as titan dioxide or zinc selenide. OVD Kinegram Corp, Switzerland

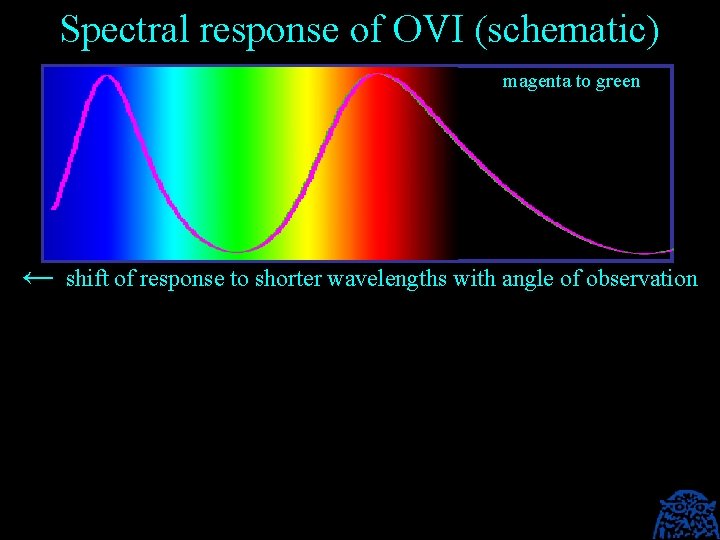
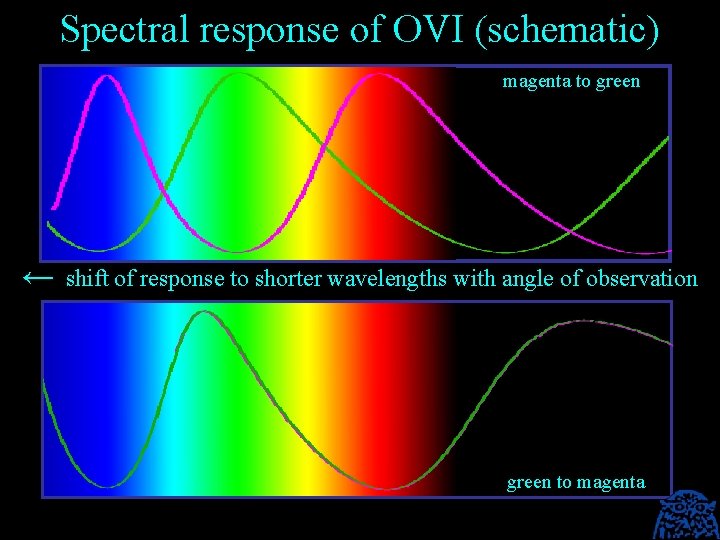
Colour shift and refractive index of Optically Variable Ink (OVI) The next slides show that the large color shift of OVI is based on the low refractive index of magnesium fluoride (n = 1. 38). On itself, this would render the thin film a reflection about as low as that of water (n = 1. 33). However, by adding a reflective aluminum layer and a semireflective chromium layer, the structure becomes a highly efficient iridescent reflector, often called a Fabry-Perot interference filter or Fabry-Perot etalon. The thickness of the magnesium fluoride layer defines the particular color shift of the thin film. In order to make the OVI flakes independent of orientation on printing, the thin film structure has been made symmetric.

Optically Variable Ink (OVI) Cr Mg. F 2 5 nm (variable thickness) n = 1, 38 Al Mg. F 2 30 nm Low refractive index (variable thickness) n = 1, 38 Cr 5 nm Medium: transparent ink

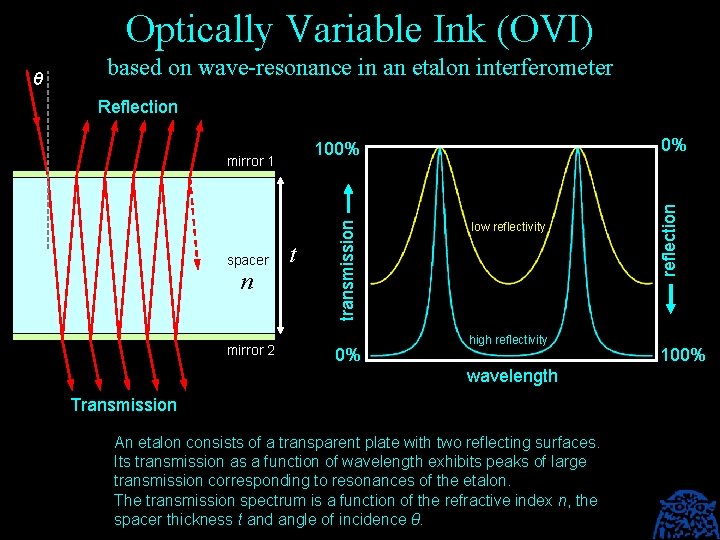
Optically Variable Ink (OVI) based on wave-resonance in an etalon interferometer Reflection n mirror 2 t 0% low reflectivity high reflectivity wavelength Transmission An etalon consists of a transparent plate with two reflecting surfaces. Its transmission as a function of wavelength exhibits peaks of large transmission corresponding to resonances of the etalon. The transmission spectrum is a function of the refractive index n, the spacer thickness t and angle of incidence θ. reflection mirror 1 spacer 0% 100% transmission θ 100%

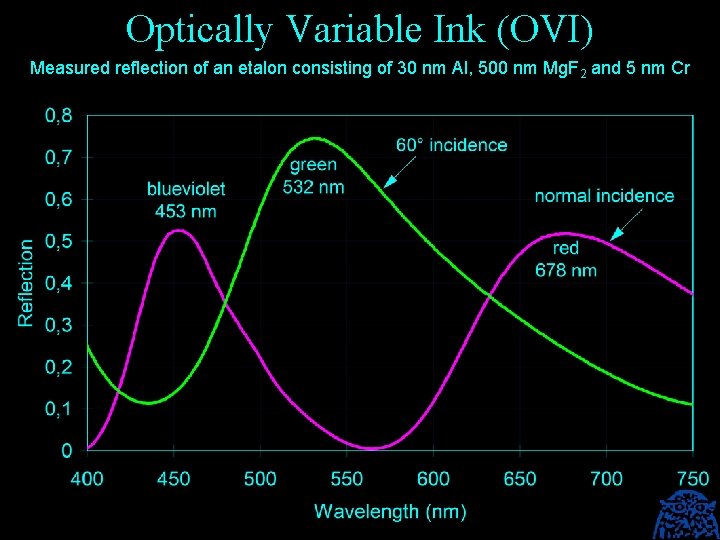
Optically Variable Ink (OVI) Measured reflection of an etalon consisting of 30 nm Al, 500 nm Mg. F 2 and 5 nm Cr

Optically Variable Ink (OVI) Swiss passport, detail 14 x 19 mm

Spectral response of OVI (schematic) magenta to green ← shift of response to shorter wavelengths with angle of observation

Spectral response of OVI (schematic) magenta to green ← shift of response to shorter wavelengths with angle of observation green to magenta

End of presentation