Refraction How Entering a New Medium Affects Light

Refraction How Entering a New Medium Affects Light

Broad Sense Refraction • When light enters a new medium, it will change speeds based upon the ability of the light of move through the new medium. More specifically, we will look at the mathematics when light enters a new medium.

c=fλ speed = (freq)(wavelength) • Substances transmit light differently. • Index of Refraction, n, a relative measure of how fast light will propagate (travel)in a medium. Higher number, slower the light moves. For air n = 1. 00 n = c/v c = 3. 0 x 108 m/s. (EQ 1) With this slowdown, something else must change about the wave as well.

• The frequency must remain constant otherwise waves would be destroyed or stack up at boundary. • n 1λ 1 = n 2λ 2 (EQ 2) • To find new wavelength of light traveling in new medium

• When a ray of light strikes a new medium obliquely (at an angle)the direction of the ray in the new medium, the refracted ray, will be different than the incident ray.

Angles measured to the Normal • Snell’s Law: • n 1 sin Θi = n 2 sin Θr Where Θi is the angle of incidence, Θr the angle of refraction as measured to the Normal of the interface between the two media. • If n 1< n 2 Θr < Θi • If n 1> n 2 Θr > Θi

• It turns out that in reality, the index of refraction for a substance is dependent upon the wavelength of light. From the EQ 2 above, λ and n are inversely related. For specific wavelengths, as wavelength decreases, index of refraction increases. This phenomena of varying index of refraction is known as dispersion. Dispersion leads to the such things as rainbows.

• When white light enters a triangular prism it will be separated into varying component colors because each different wavelength will be refracted by a different amount. With shorter wavelengths being refracted more; Yielding the spectrum.

White light enters the raindrop where the edges of the drop refract each wavelength differently with the angles for red (highest λ) and violet (shortest) Being the two extremes. The red will hit your eye while the violet will be above your head, and at the bottom of the rainbow, the violet will catch your eye while the red will be below.

• Drops at top of rainbow yield red rays to eyes, while at bottom, only violet encounters eye.

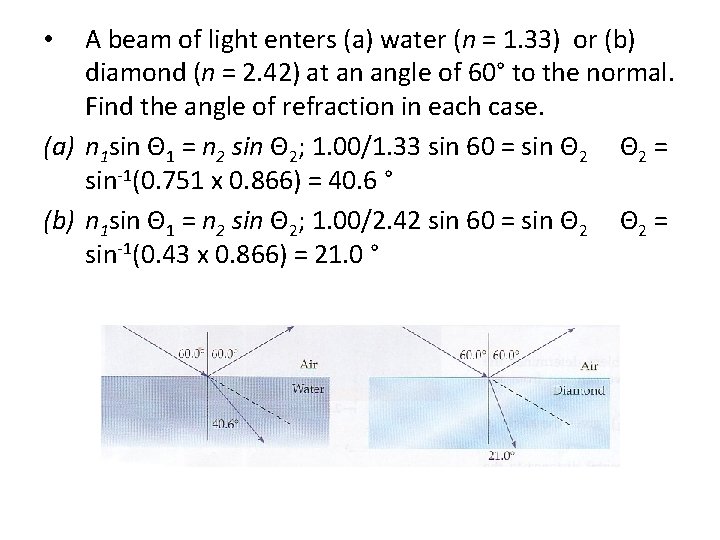
A beam of light enters (a) water (n = 1. 33) or (b) diamond (n = 2. 42) at an angle of 60° to the normal. Find the angle of refraction in each case. (a) n 1 sin Θ 1 = n 2 sin Θ 2; 1. 00/1. 33 sin 60 = sin Θ 2 = sin-1(0. 751 x 0. 866) = 40. 6 ° (b) n 1 sin Θ 1 = n 2 sin Θ 2; 1. 00/2. 42 sin 60 = sin Θ 2 = sin-1(0. 43 x 0. 866) = 21. 0 ° •

• Some light will reflect back into the denser medium. As Θ 1 increases, Θ 2 increases as well. Eventually Θ 1 will be such that Θ 2 will be 90° (all light will refract along boundary). This incident angle is known as the critical angle, and when Θ 1 is greater than the critical angle, all the light will be reflected back into the denser medium, a state known as total internal reflection. • sin Θcrit = n 2 /n 1

• Total internal reflection can only occur when light moves from a more dense medium to a less dense medium. ( From higher index of refraction to lower) • Find the critical angle for light moving from glass (n = 1. 50) into (a) air (n= 1. 00) and (b) water (n = 1. 33) • sin-1 n 2/n 1 = sin-1 1/1. 5 = 41. 8° • sin-1 n 2/n 1 = sin-1 1. 33/1. 5 = 62. 5°