Refraction Corrections for Surface Integral Methods in Jet

Refraction Corrections for Surface Integral Methods in Jet Aeroacoustics Fong. Loon Pan Purdue University, West Lafayette, IN Ali Uzun Florida State University, Tallahassee, FL Anastasios Lyrintzis Purdue University, West Lafayette, IN 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 1

Outline Surface Integral Methods – Porous FW-H method Refraction Corrections – – Simple geometric acoustics theory (GA) Lilley’s equation Validation (Simple point source) Application (Jet noise prediction using LES) Conclusions 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 2

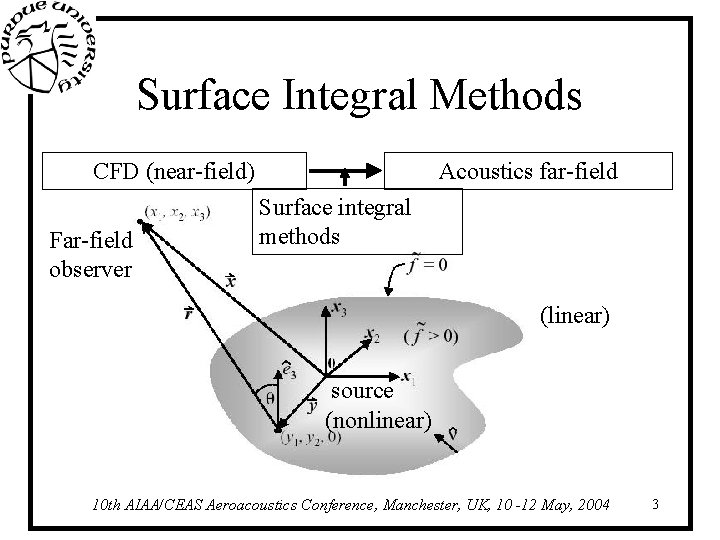
Surface Integral Methods CFD (near-field) Far-field observer Acoustics far-field Surface integral methods (linear) source (nonlinear) 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 3

Porous FW-H Method (Time Domain) where 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 4

Porous FW-H Method (Frequency Domain) and are Fourier transform of Lr and Un 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 5

Jet Noise Predictions • S cannot surround the entire source region • MGB can be used outside S • Refraction corrections (predict zone of silence) 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 6

Simple Geometric Acoustics (GA) Ray Theory (1977) • Refraction of sound through thick cylindrical shear layer • Acoustic wavelength < shear layer thickness • Ray angle & amplitude correction 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 From Papamochou 7

Simple Geometric Acoustics (GA) Ray Theory Asymmetric parallel shear flow U : the velocity at the downstream end of the control surface : the sound emission angle with respect to the jet axis : the emission angle in the ambient air 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 8

Lilley’s Equation (1974) where P : acoustic pressure fluctuation normalized by G : acoustic source distribution : mean flow velocity 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 9

Lilley’s Equation xs : Green’s function associated to Fourier transformed solution of Lilley’s wave equation : source position 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 10

High-Frequency Asymptotic Approximations Assumptions: • Distance between source and jet centerline axis is sufficiently large (i. e. several factors of 1/ko), R (ko is streamwise wavenumber, ko = w/ao) Critical azimuthal wavenumber, n can be scaled to the order of ko i. e. (Asymmetric, high-frequency) As source moves closer to the jet centerline axis i. e. (Quasi-symmetric, high-frequency) 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 11

Lilley’s Approximation Solutions : reduced Green’s function : free-space Green’s function 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 12

Asymmetric, Far-field Approximation where 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 13

Quasi-symmetric, Far-field Approximation where 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 14

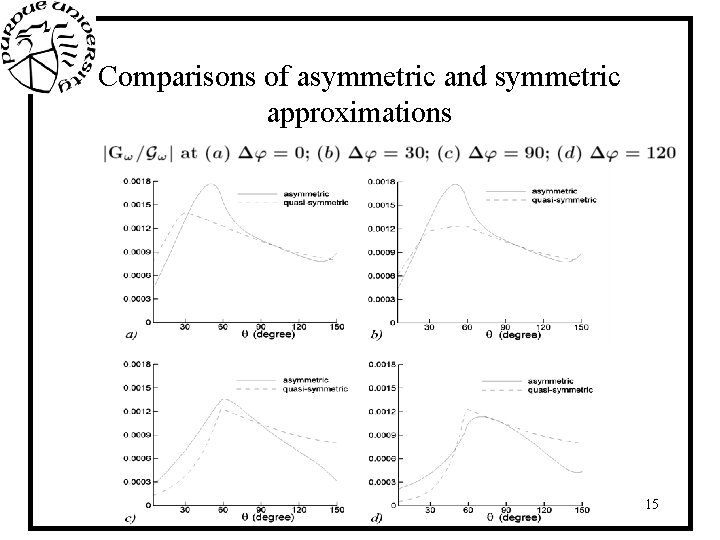
Comparisons of asymmetric and symmetric approximations 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 15

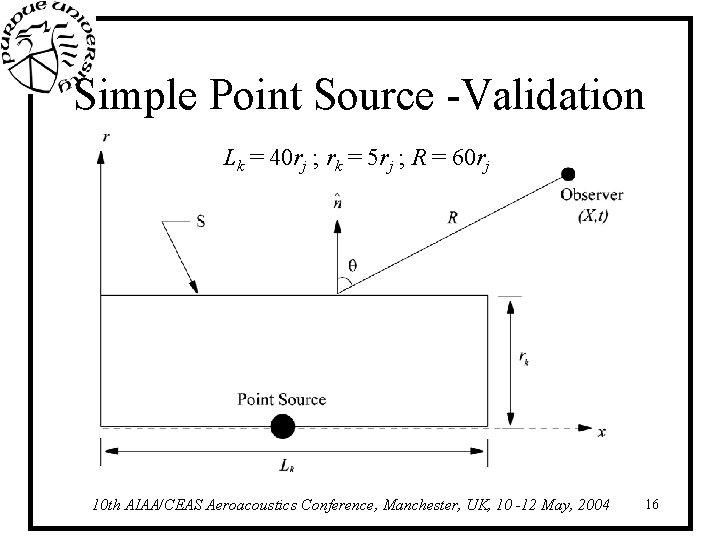
Simple Point Source -Validation Lk = 40 rj ; rk = 5 rj ; R = 60 rj 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 16

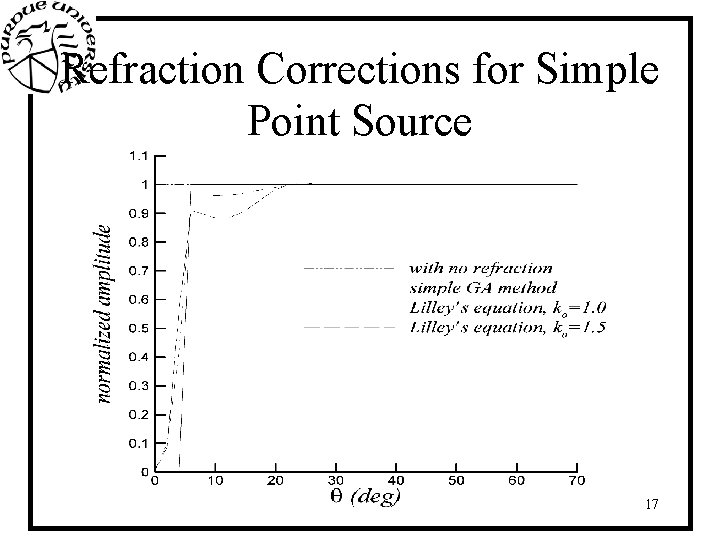
Refraction Corrections for Simple Point Source 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 17

Mach 0. 9, Reynolds Number 400, 000 Isothermal Jet LES • • 6 -th order compact spatial differencing 6 -th order compact spacial filter No explicit SGS model 15. 6 million grid points Streamwise length 35 ro ; width and height 30 ro 50, 000 time steps 5. 5 days of run time using 200 POWER 3 processors on an IBM-SP 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 18

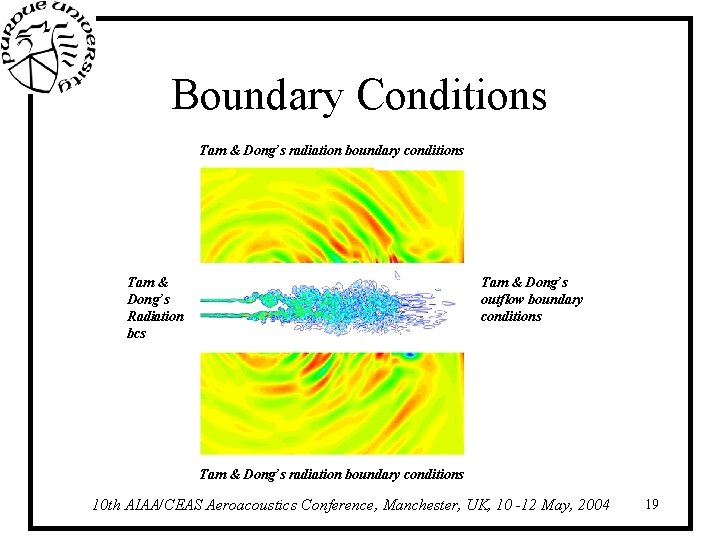
Boundary Conditions Tam & Dong’s radiation boundary conditions Tam & Dong’s Radiation bcs Tam & Dong’s outflow boundary conditions Tam & Dong’s radiation boundary conditions 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 19

FW-H Control Surface 7. 8 rj 30 rj 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 20

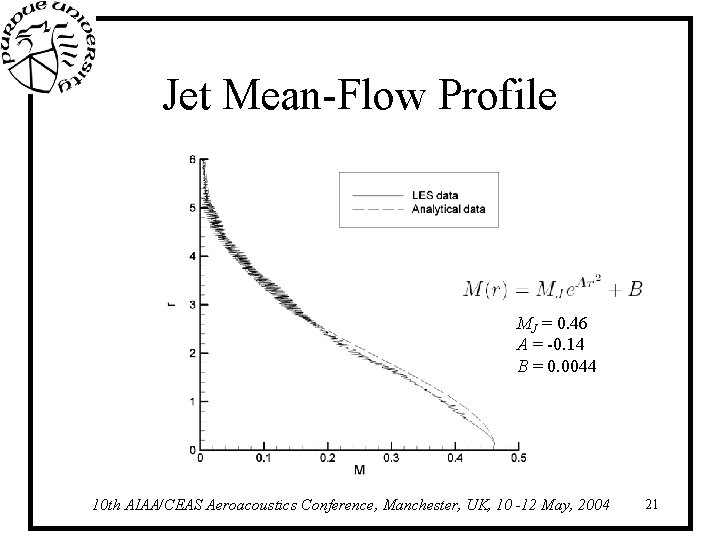
Jet Mean-Flow Profile MJ = 0. 46 A = -0. 14 B = 0. 0044 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 21

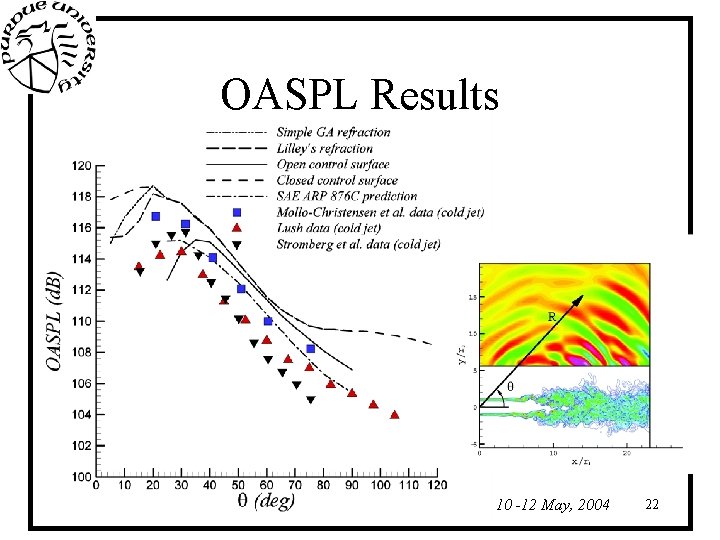
OASPL Results 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 22

Jet Aeroacoustics • Acoustic data collected every 5 time steps over a period of 25, 000 time steps • Maximum Strouhal numbers resolved (based on grid spacing) St=3. 0 • Open surface: shallow angles ( ) not accurate, since streamwise control surface is relatively short • Closed surface: spurious effects at ( ) due to a line of dipoles on the outflow surface, as quadrupoles exit the domain 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 23

Lighthill Code • Code employs the time derivative formulation of Lighthill’s volume integral • Uses the time history of the jet flow data provided by the 3 -D LES code • 8 th-order accurate explicit scheme to compute the time derivatives • Cubic spline interpolation to evaluate the source term at retarded times 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 24

Lighthill Code (continued) • Time accurate data was saved inside the jet at every 10 time steps over a period of 40, 000 time steps • 1. 2 Terabytes (TB) of total data to process • Used 1160 processors in parallel for the volume integrals • Cut-off frequency corresponds to Strouhal number 4. 0 due to the fine grid spacing inside the jet 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 25

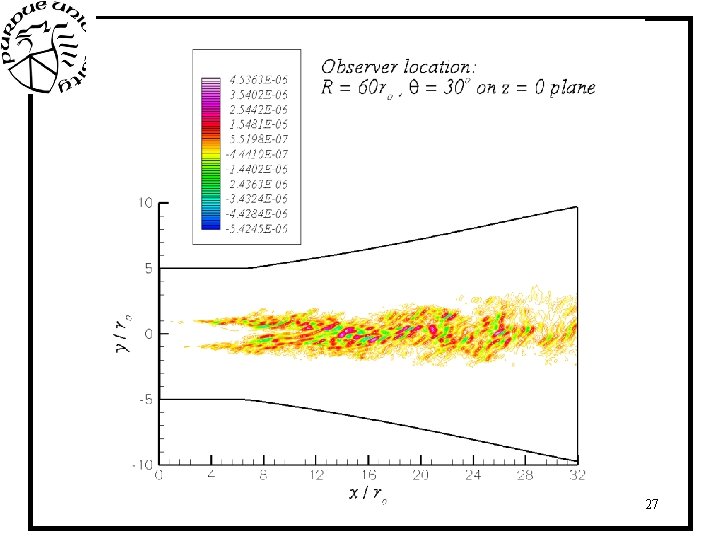
Animation • Animation on the next slide shows the time variation of the Lighthill sources that radiate noise in the direction of the observer located at R = 60 ro, q = 30 o on the far-field arc 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 26

10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 27

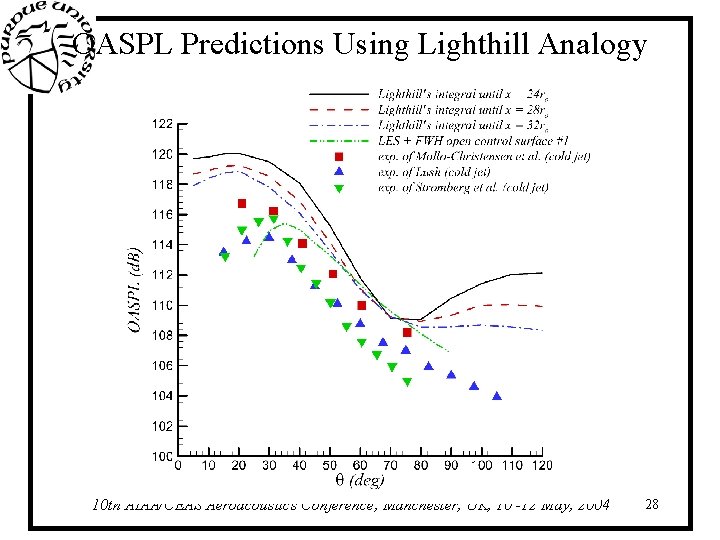
OASPL Predictions Using Lighthill Analogy 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 28

Conclusions • Simple GA method and Lilley’s equation are added to the surface integral methods to predict zone of silence • Jet noise LES results were improved • GA method is simpler, but does not take azimuthal variation into account • Lilley’s equation is up to 60 times more expensive 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 29

The End 10 th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10 -12 May, 2004 30