Reflections What will we accomplish in todays lesson

Reflections

What will we accomplish in today’s lesson? • • Given a pre-image and its reflected image, determine the line of reflection. Given a pre-image and its reflected image graphed on the coordinate plane, determine the line of reflection and give a function rule for the reflection. Given the line of reflection, draw a reflection on plain paper. Given a horizontal or vertical line of reflection or function rule, draw a reflection on the coordinate plane. Reflections • A reflection is a transformation that flips a figure across a line, called the line of reflection. • Segments connecting corresponding points of a pre-image and its reflected image are bisected by the line of reflection. • Corresponding points of a pre-image and its reflected image are equidistant from the line of reflection. • The reflection of a figure changes orientation so that it faces in the opposite direction of the original figure.

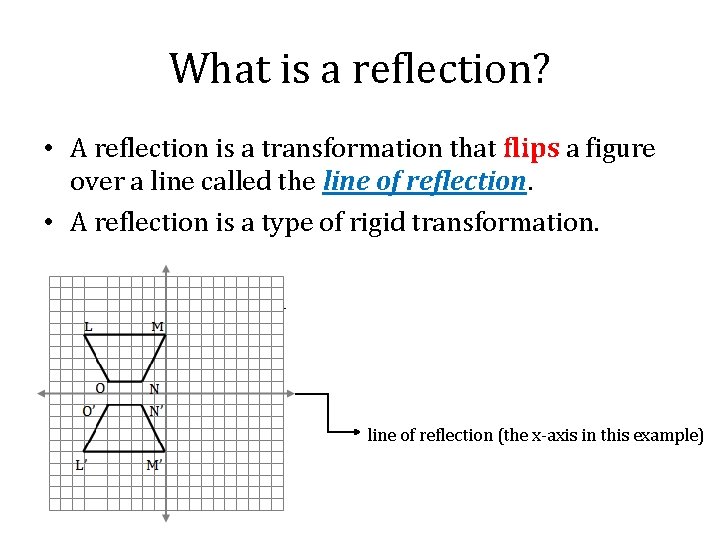
What is a reflection? • A reflection is a transformation that flips a figure over a line called the line of reflection. • A reflection is a type of rigid transformation. line of reflection (the x-axis in this example)

Properties of Reflections • Segments connecting corresponding points of a pre-image and its reflected image are bisected by the line of reflection.

Properties of Reflections • Corresponding points of a pre-image and its reflected image are equidistant from the line of reflection. • The reflection of a figure changes orientation so that it faces in the opposite direction of the original figure.

Coordinate notation for reflections in the coordinate plane 3 rules for reflections in a coordinate plane • reflection across the x-axis: (x, y) (x, -y) • reflection across the y-axis: (x, y) (-x, y) • reflection across the line y=x: (x, y) (y, x)

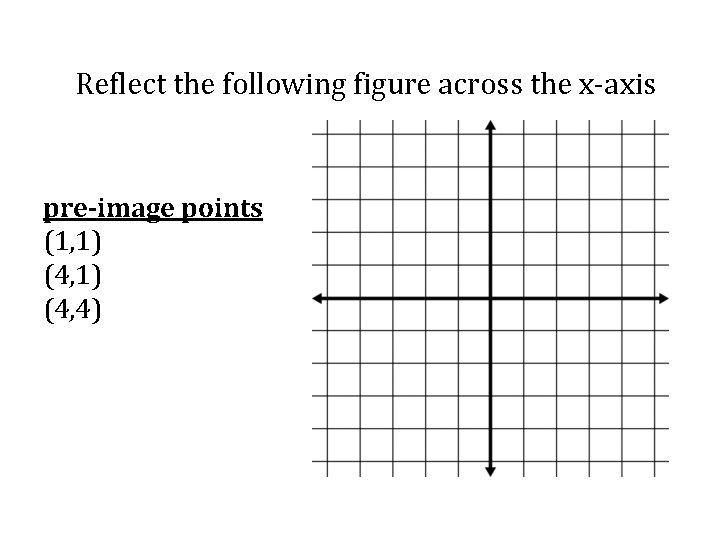
Reflect the following figure across the x-axis pre-image points (1, 1) (4, 4)

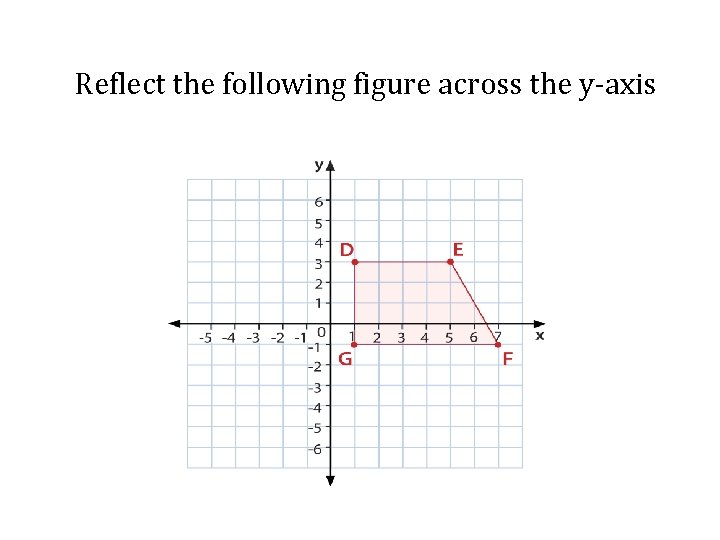
Reflect the following figure across the y-axis

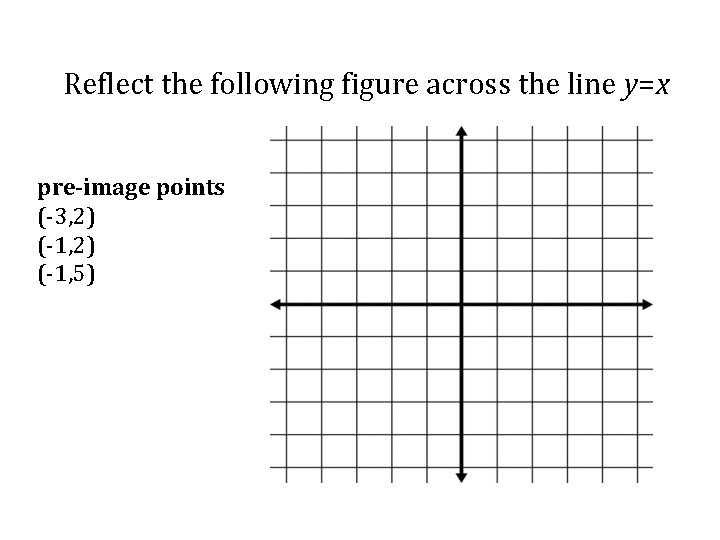
Reflect the following figure across the line y=x pre-image points (-3, 2) (-1, 5)

Options for the line of reflection • A reflection can occur across any line. • It is not limited just to the x-axis, y-axis, and line y=x.

Identifying the equation for the line of reflection helps to see the change between the coordinates of the pre-image and image. The line of reflection is represented by the equation x = -2. To begin, find the distance from the pre-image point to the line of reflection. Each image point must be that same distance in the opposite direction from the line of reflection. For example, point A is 3 units from the line of reflection. So A' must be three units in the opposite direction from the line of reflection.

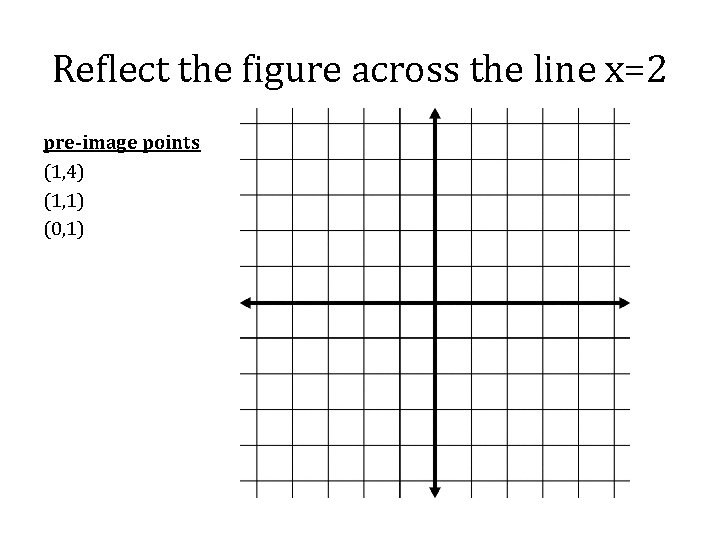
Reflect the figure across the line x=2 pre-image points (1, 4) (1, 1) (0, 1)

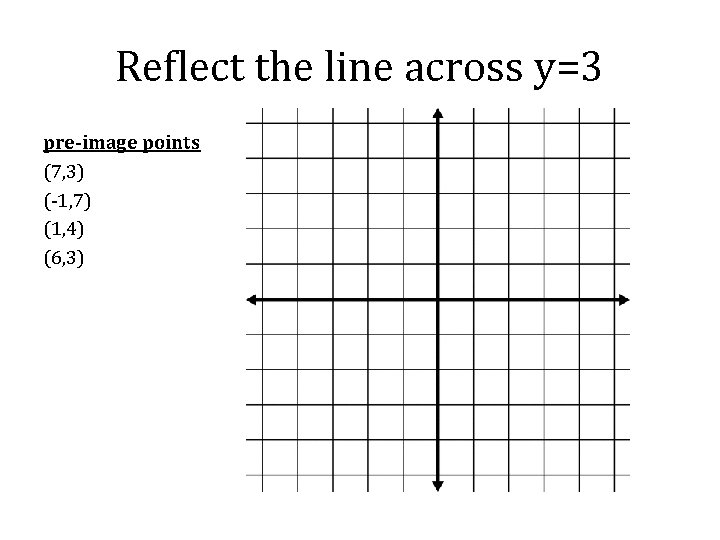
Reflect the line across y=3 pre-image points (7, 3) (-1, 7) (1, 4) (6, 3)

Try it yourself! • http: //www. shodor. org/interactivate/activi ties/Transmographer/