Reflection Symmetry and EnergyLevel Ordering of Frustrated Ladder



![Outline of the Proof [Lieb & Mattis, 1962] The spin of can be found Outline of the Proof [Lieb & Mattis, 1962] The spin of can be found](https://slidetodoc.com/presentation_image_h2/7db74e4eaf49ea94cc42ee22c491e40e/image-7.jpg)

![Frustrated Spin-1/2 Ladder: Generalized Lieb-Mattis Theorem [T. Hakobyan, Phys. Rev. B 75, 214421 (2007)] Frustrated Spin-1/2 Ladder: Generalized Lieb-Mattis Theorem [T. Hakobyan, Phys. Rev. B 75, 214421 (2007)]](https://slidetodoc.com/presentation_image_h2/7db74e4eaf49ea94cc42ee22c491e40e/image-11.jpg)




- Slides: 17

Reflection Symmetry and Energy-Level Ordering of Frustrated Ladder Models The extension of Lieb-Mattis theorem [1962] to a frustrated spin system Tigran Hakobyan Yerevan State University & Yerevan Physics Institute T. Hakobyan, Phys. Rev. B 75, 214421 (2007)

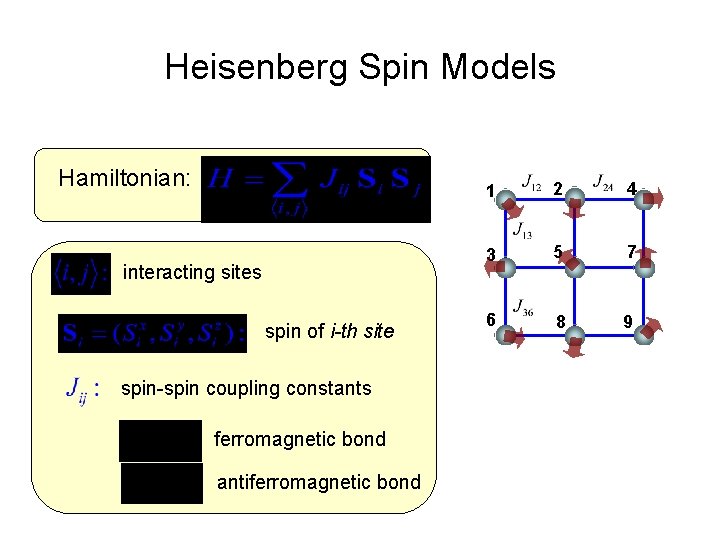
Heisenberg Spin Models Hamiltonian: interacting sites spin of i-th site spin-spin coupling constants ferromagnetic bond antiferromagnetic bond 1 2 4 3 5 7 6 8 9

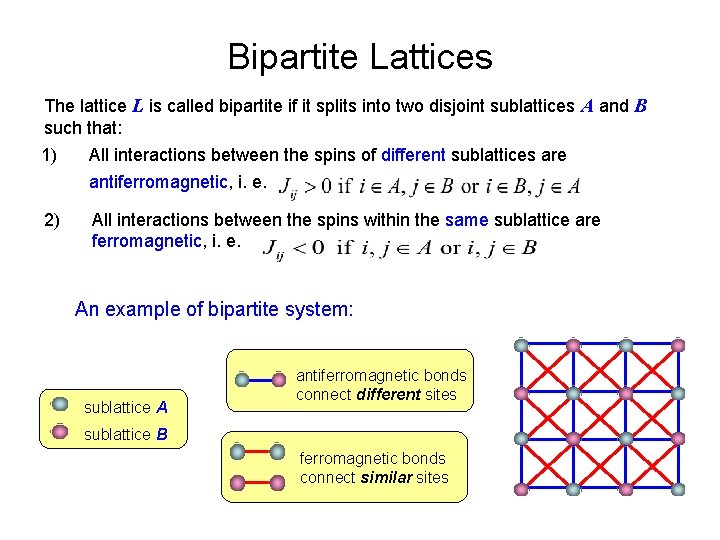
Bipartite Lattices The lattice L is called bipartite if it splits into two disjoint sublattices A and B such that: 1) All interactions between the spins of different sublattices are antiferromagnetic, i. e. 2) All interactions between the spins within the same sublattice are ferromagnetic, i. e. An example of bipartite system: sublattice A antiferromagnetic bonds connect different sites sublattice B ferromagnetic bonds connect similar sites

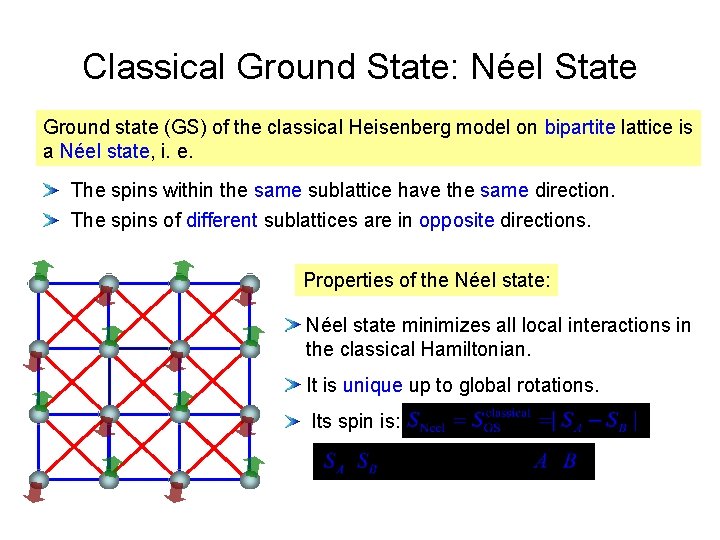
Classical Ground State: Néel State Ground state (GS) of the classical Heisenberg model on bipartite lattice is a Néel state, i. e. The spins within the same sublattice have the same direction. The spins of different sublattices are in opposite directions. Properties of the Néel state: Néel state minimizes all local interactions in the classical Hamiltonian. It is unique up to global rotations. Its spin is:

Quantum GS: Lieb-Mattis Theorem The quantum fluctuations destroy Néel state and the ground state (GS) of quantum system has more complicated structure. However, for bipartite spin systems, the quantum GS inherits some properties of its classical counterpart. Lieb & Mattis [J. Math. Phys. 3, 749 (1962)] proved that The quantum GS of a finite-size system is a unique multiplet with total spin , i. e. The lowest-energy . in the sector, where the total spin is equal to S, is a monotone increasing function of S for any [antiferromagnetic ordering of energy levels]. All lowest-energy spin-S states form one multiplet for [nondegeneracy of the lowest levels].

Steps of the Proof Perron-Frobenius theorem: The lowest eigenvalue of any connected matrix having negative or vanishing off-diagonal elements is nondegenerate. Correponding eigenvector is a positive superposition of all basic states. After the rotation of all spins on one sublattice on reads generate negative off-diagonal elements The matrix of Hamiltonian being restricted to any connected in the standard Ising basis. Perron-Frobenius theorem is applied to any Relative GS , the Hamiltonian are diagonal subspace is subspace:
![Outline of the Proof Lieb Mattis 1962 The spin of can be found Outline of the Proof [Lieb & Mattis, 1962] The spin of can be found](https://slidetodoc.com/presentation_image_h2/7db74e4eaf49ea94cc42ee22c491e40e/image-7.jpg)
Outline of the Proof [Lieb & Mattis, 1962] The spin of can be found by constructing a trial state being a positive superposition of (shifted) Ising basic states and having a definite value of the spin. Then it will overlap with. The uniqueness of the relative GS then implies that both states have the same spin. As a result, The multiplet containing all states with spin has the lowest-energy value. It it nondegenerate. Antiferromagnetic ordering of energy levels: The ground state is a unique multiplet with spin among

Generalizations The Lieb-Mattis theorem have been generalized to: • Ferromagnetic Heisenberg spin chains B. Nachtergaele and Sh. Starr, Phys. Rev. Lett. 94, 057206 (2005) • SU(n) symmetric quantum chain with defining representation T. Hakobyan, Nucl. Phys. B 699, 575 (2004) • Spin-1/2 ladder model frustrated by diagonal interaction T. Hakobyan, Phys. Rev. B 75, 214421 (2007) The topic of this talk

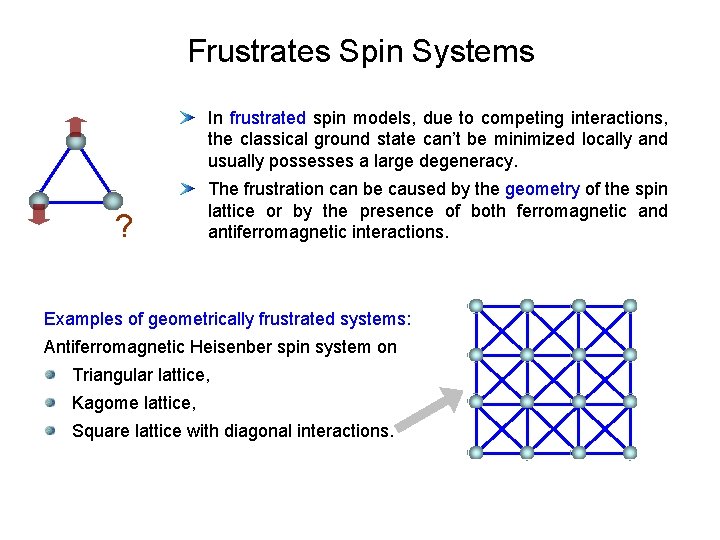
Frustrates Spin Systems In frustrated spin models, due to competing interactions, the classical ground state can’t be minimized locally and usually possesses a large degeneracy. ? The frustration can be caused by the geometry of the spin lattice or by the presence of both ferromagnetic and antiferromagnetic interactions. Examples of geometrically frustrated systems: Antiferromagnetic Heisenber spin system on Triangular lattice, Kagome lattice, Square lattice with diagonal interactions.

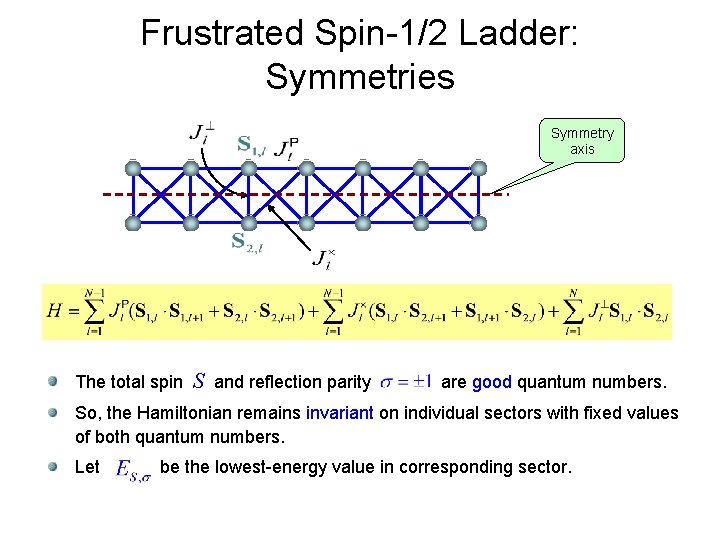
Frustrated Spin-1/2 Ladder: Symmetries Symmetry axis The total spin S and reflection parity are good quantum numbers. So, the Hamiltonian remains invariant on individual sectors with fixed values of both quantum numbers. Let be the lowest-energy value in corresponding sector.
![Frustrated Spin12 Ladder Generalized LiebMattis Theorem T Hakobyan Phys Rev B 75 214421 2007 Frustrated Spin-1/2 Ladder: Generalized Lieb-Mattis Theorem [T. Hakobyan, Phys. Rev. B 75, 214421 (2007)]](https://slidetodoc.com/presentation_image_h2/7db74e4eaf49ea94cc42ee22c491e40e/image-11.jpg)
Frustrated Spin-1/2 Ladder: Generalized Lieb-Mattis Theorem [T. Hakobyan, Phys. Rev. B 75, 214421 (2007)] N = number of rungs The minimum-energy levels are nondegenerate (except perhaps the one with and ) and are ordered according to the rule: The ground state in entire sector is a spin singlet while in sector is a spin triplet. In both cases it is unique.

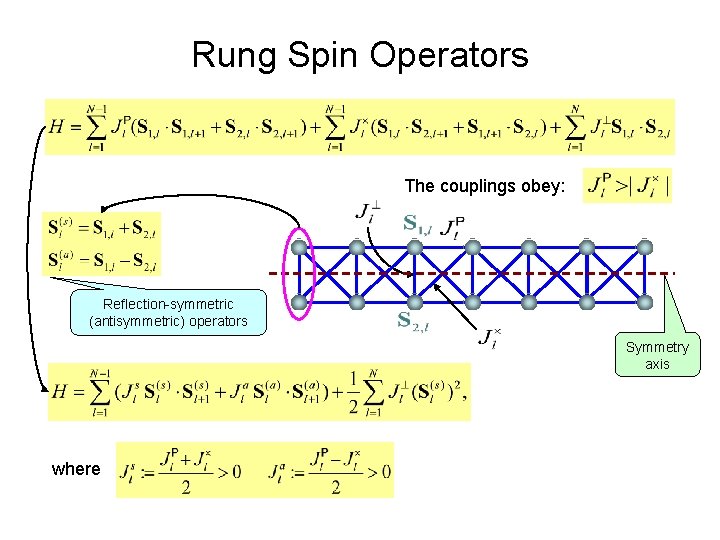
Rung Spin Operators The couplings obey: Reflection-symmetric (antisymmetric) operators Symmetry axis where

Construction of Nonpositive Basis: Rung Spin States We use the following basis for 4 rung states: Rung singlet 1) Rung triplet We use the basis constructed from rung singlet and rung triplet states: The reflection operator R is diagonal in this basis. the number of rung singlets. Define unitary operator, which rotates the odd-rung spins around where z axis on is

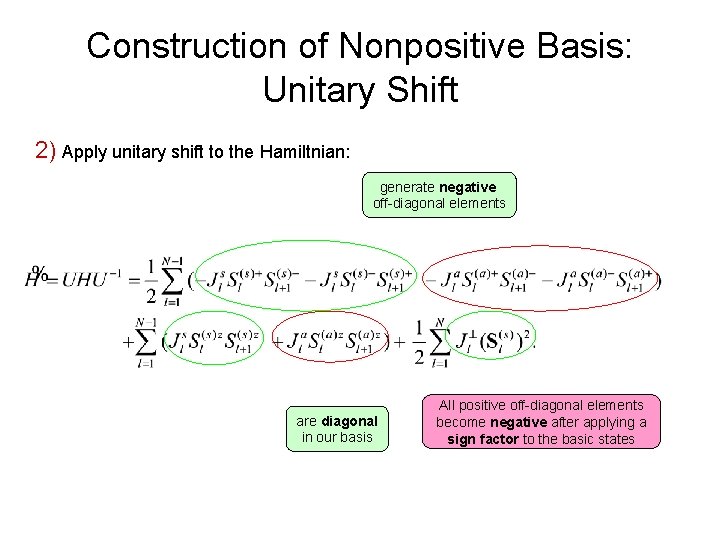
Construction of Nonpositive Basis: Unitary Shift 2) Apply unitary shift to the Hamiltnian: generate negative off-diagonal elements are diagonal in our basis All positive off-diagonal elements become negative after applying a sign factor to the basic states

Construction of Nonpositive Basis: Sign Factor 3) It can be shown that all non-diagonal matrix elements of become nonpositive in the basis = the number of pairs in the sequence is on the left hand side from = the number of rung singlets . in where

Subspaces and Relative Ground States Due to and reflection R symmetries, the Hamiltonian is invariant on each subspace with the definite values of spin projection and reflection operators, which we call subspace: The matrix of the Hamiltonian in the basis being restricted on any subspace is connected [easy to verify]. Perron-Frobenius theorem can be applied to subspace: The relative ground state of in subspace is unique and is a positive superposition of all basic states:

Relative ground states The spin of can be found by constructing a trial state being a positive superposition of defined basic states and having a definite value of the spin. Then it will overlap with. The uniqueness of the relative GS then implies that both states have the same spin. As a result,
 Total internal reflection
Total internal reflection Total internal reflection
Total internal reflection Frustrated total internal reflection touch screen
Frustrated total internal reflection touch screen Diffuse reflection vs regular reflection
Diffuse reflection vs regular reflection Metric shuffle ladder
Metric shuffle ladder Frustrated freemen and bacon's rebellion
Frustrated freemen and bacon's rebellion Order of rotational symmetry
Order of rotational symmetry Glide reflectional symmetry
Glide reflectional symmetry 7.g rotation vs translation
7.g rotation vs translation Freight
Freight Frustrated simile
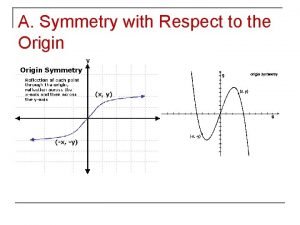
Frustrated simile The graph is symmetric with respect to the origin
The graph is symmetric with respect to the origin Representing comparing and ordering decimals
Representing comparing and ordering decimals Ordering fractions decimals and percentages
Ordering fractions decimals and percentages Describe generic-specific-ordering of hypotheses.
Describe generic-specific-ordering of hypotheses. How do you compare and order integers
How do you compare and order integers Time clocks and the ordering of events
Time clocks and the ordering of events Ordering fractions decimals and percentages gcse questions
Ordering fractions decimals and percentages gcse questions