Reflection Plane Mirrors Curved Mirrors Refraction Snells Law

§ Reflection – Plane Mirrors – Curved Mirrors § Refraction – Snell’s Law – Dispersion § Total Internal Reflection – Critical angle Reeves Chapters 14 -15

Light Rays A point source of light emits spherical waves in all directions. Each circle represents a wave front or crest of a wave. Rays are: perpendicular to wave fronts point in the direction of wave travel are straight lines If we are far enough away from the light source, the spherical wave front looks flat. plane waves Note that for plane waves: wave fronts are parallel to each other rays are parallel to each other and to wave fronts Reeves Chapters 14 -15

Geometrical Optics § We assume that light follows straightline paths (rays) § Changes occur when a ray hits a boundary – ray may bounce off (reflection) – ray may bend into the other medium (refraction) – ray may be absorbed (light energy thermal energy) Reeves Chapters 14 -15

Angles are Measured from the Normal In geometrical optics, angles are always measured Inc ide nt ray 30 normal with respect to the normal of the interface 60 o o Reeves Chapters 14 -15 interface

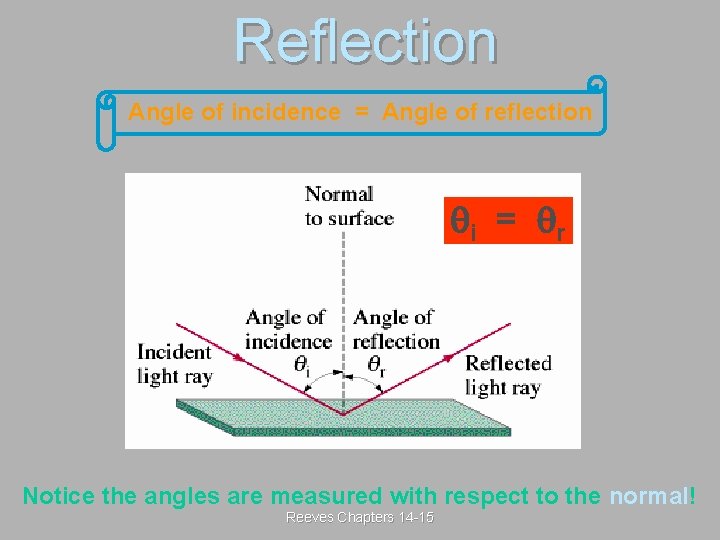
Reflection Angle of incidence = Angle of reflection i = r Notice the angles are measured with respect to the normal! Reeves Chapters 14 -15

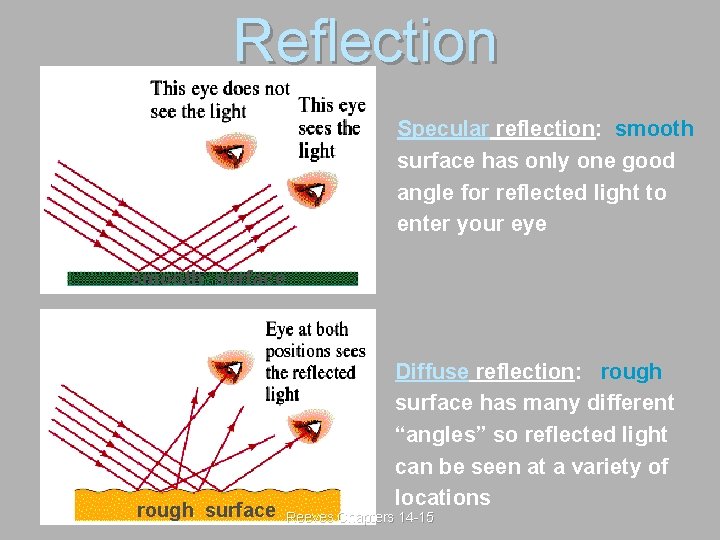
Reflection Specular reflection: smooth surface has only one good angle for reflected light to enter your eye smooth surface rough surface Diffuse reflection: rough surface has many different “angles” so reflected light can be seen at a variety of locations Reeves Chapters 14 -15

§ Conundrum 1(Post) 1 (1) the Moon is very large When watching the Moon over the ocean, you often see a long streak of light on the surface of the water. This occurs because: (2) atmospheric conditions are just right (3) the ocean is calm (4) the ocean is wavy (5) motion of the Moon Reeves Chapters 14 -15

§ Conundrum 1(ans) 1 (1) the Moon is very large When watching the Moon over the ocean, you often see a long streak of light on the surface of the water. This occurs because: (2) atmospheric conditions are just right (3) the ocean is calm (4) the ocean is wavy (5) motion of the Moon When the water surface changes, the angle of incidence also changes. Thus, different spots on the water can reflect the Moon into your eyes at different times. Reeves Chapters 14 -15

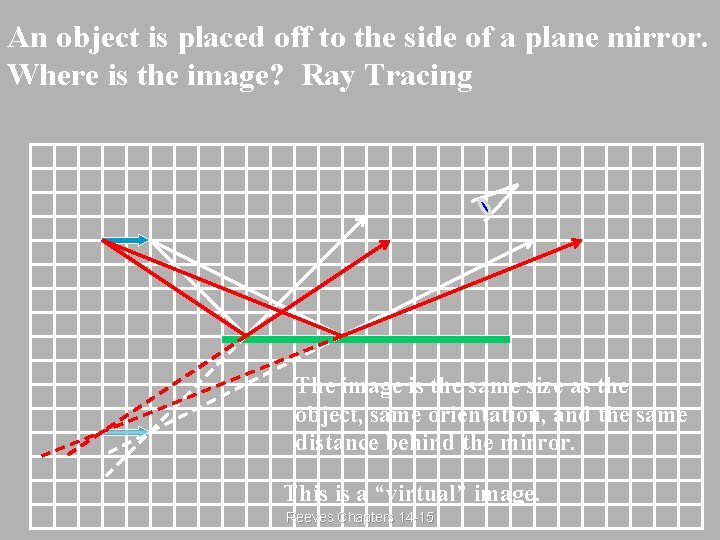
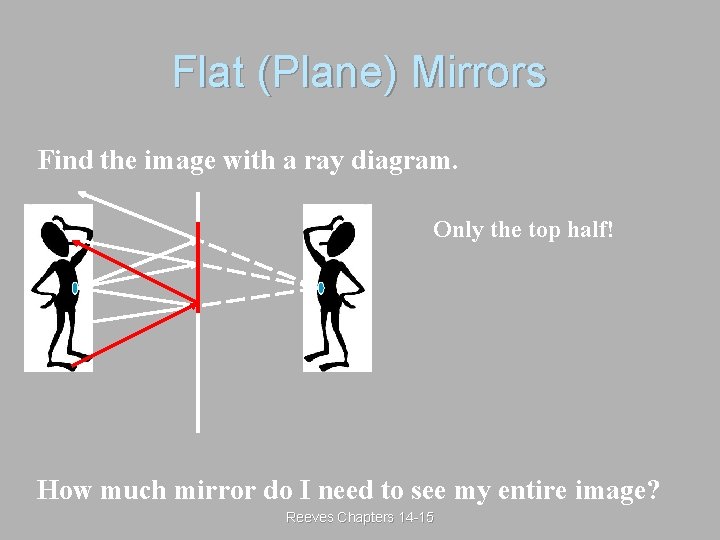
An object is placed off to the side of a plane mirror. Where is the image? Ray Tracing The image is the same size as the object, same orientation, and the same distance behind the mirror. This is a “virtual” image. Reeves Chapters 14 -15

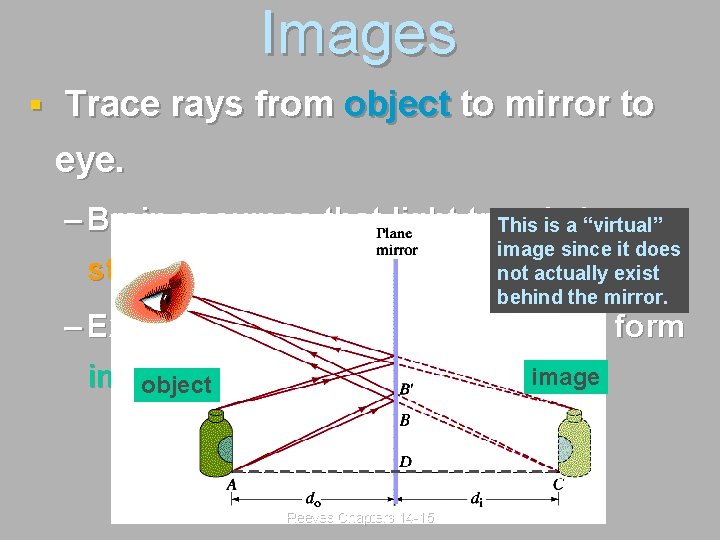
Images § Trace rays from object to mirror to eye. – Brain assumes that light travels a This is a in “virtual” image since it does not actually exist straight line !! behind the mirror. – Extend rays back behind mirror to form image. object Reeves Chapters 14 -15

§ Conundrum 2(Post) 2 An observer at point O is facing a mirror and observes a light source S. Where does the observer perceive the mirror image of the source to be located? mirror 3 O 1 S 2 4 Reeves Chapters 14 -15

§ Conundrum 2(ans) 2 An observer at point O is facing a mirror and observes a light source S. Where does the observer perceive the mirror image of the source to be located? mirror 3 O 1 S 2 Trace the light rays from the object to the mirror to the eye. Since the brain assumes that light travels in a straight line, simply extend the rays back behind the mirror to locate the image. Reeves Chapters 14 -15 4

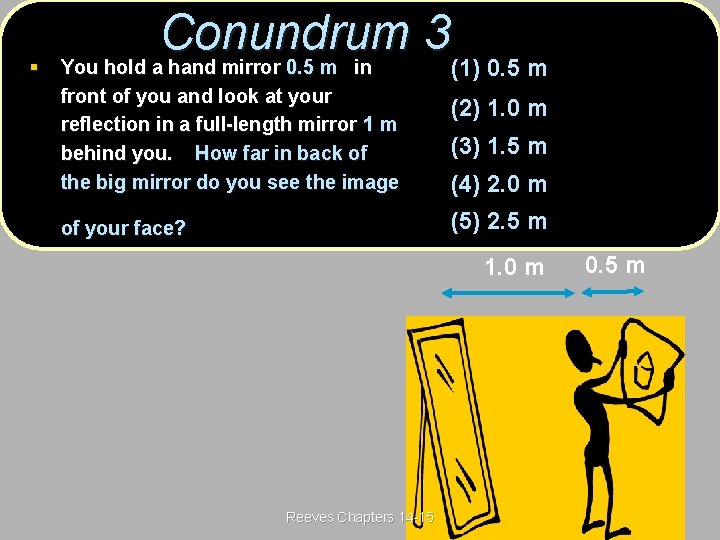
§ Conundrum 3(Post) 3 You hold a hand mirror 0. 5 m in (1) 0. 5 m front of you and look at your reflection in a full-length mirror 1 m behind you. How far in back of the big mirror do you see the image (2) 1. 0 m (3) 1. 5 m (4) 2. 0 m (5) 2. 5 m of your face? 1. 0 m Reeves Chapters 14 -15 0. 5 m

§ Conundrum 3(ans) 3 You hold a hand mirror 0. 5 m in (1) 0. 5 m front of you and look at your reflection in a full-length mirror 1 m behind you. How far in back of the big mirror do you see the image of your face? (2) 1. 0 m (3) 1. 5 m (4) 2. 0 m (5) 2. 5 m 1. 0 m The image of the face reflected in the small mirror appears 0. 5 m behind the small mirror. This image (which is the object for the big mirror) mirror is 2. 0 m away from the big mirror. So the final image is 2. 0 m behind the big mirror Reeves Chapters 14 -15 0. 5 m

Flat (Plane) Mirrors Find the image with a ray diagram. Only the top half! How much mirror do I need to see my entire image? Reeves Chapters 14 -15

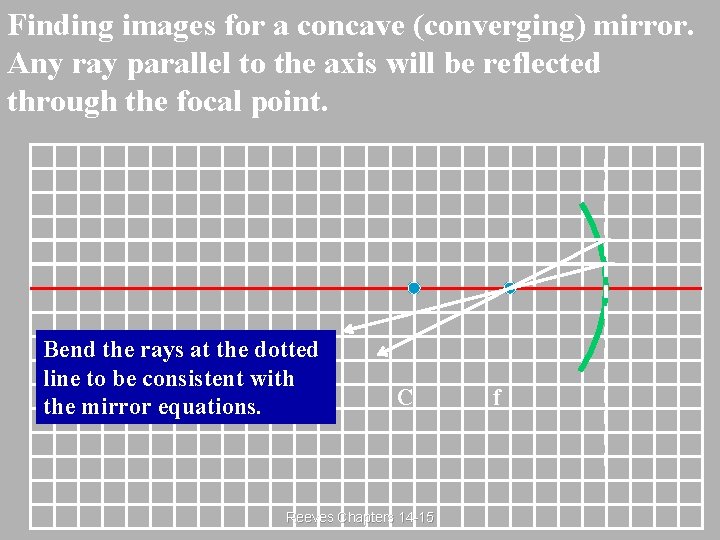
Finding images for a concave (converging) mirror. R stands for the “radius of curvature” of the mirror R Center of curvature Focal point = R/2 Reeves Chapters 14 -15

Finding images for a concave (converging) mirror. Any ray parallel to the axis will be reflected through the focal point. Bend the rays at the dotted line to be consistent with the mirror equations. C Reeves Chapters 14 -15 f

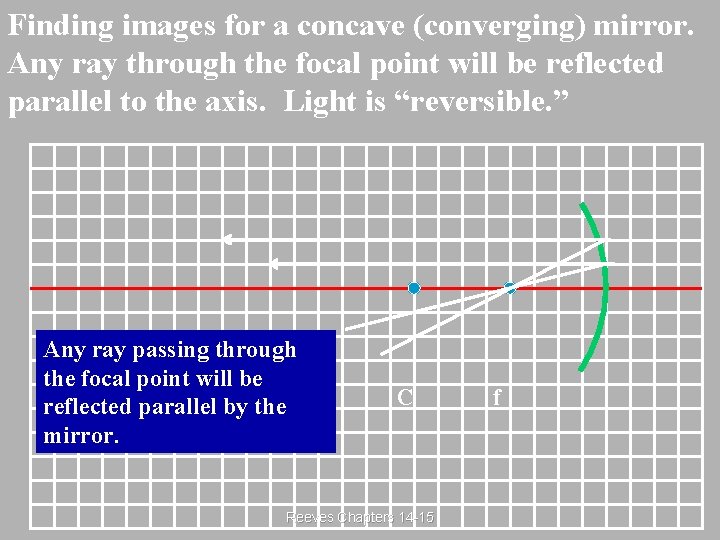
Finding images for a concave (converging) mirror. Any ray through the focal point will be reflected parallel to the axis. Light is “reversible. ” Any ray passing through the focal point will be reflected parallel by the mirror. C Reeves Chapters 14 -15 f

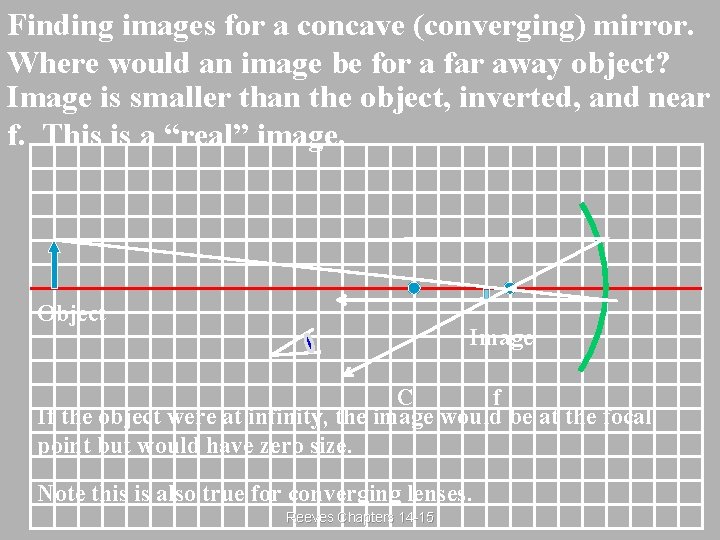
Finding images for a concave (converging) mirror. Where would an image be for a far away object? Image is smaller than the object, inverted, and near f. This is a “real” image. Object Image C f If the object were at infinity, the image would be at the focal point but would have zero size. Note this is also true for converging lenses. Reeves Chapters 14 -15

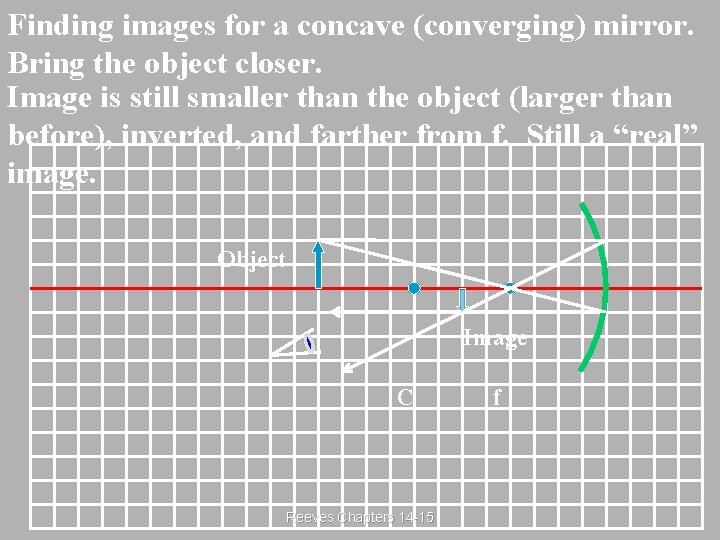
Finding images for a concave (converging) mirror. Bring the object closer. Image is still smaller than the object (larger than before), inverted, and farther from f. Still a “real” image. Object Image C Reeves Chapters 14 -15 f

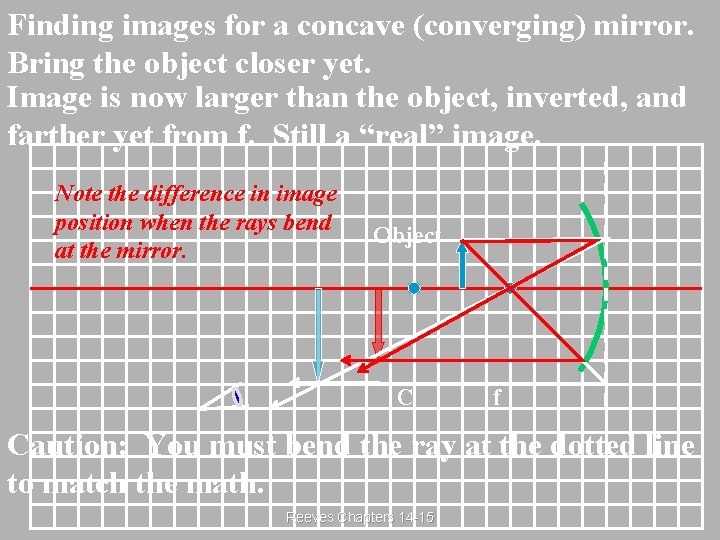
Finding images for a concave (converging) mirror. Bring the object closer yet. Image is now larger than the object, inverted, and farther yet from f. Still a “real” image. Note the difference in image position when the rays bend at the mirror. Object C f Caution: You must bend the ray at the dotted line to match the math. Reeves Chapters 14 -15

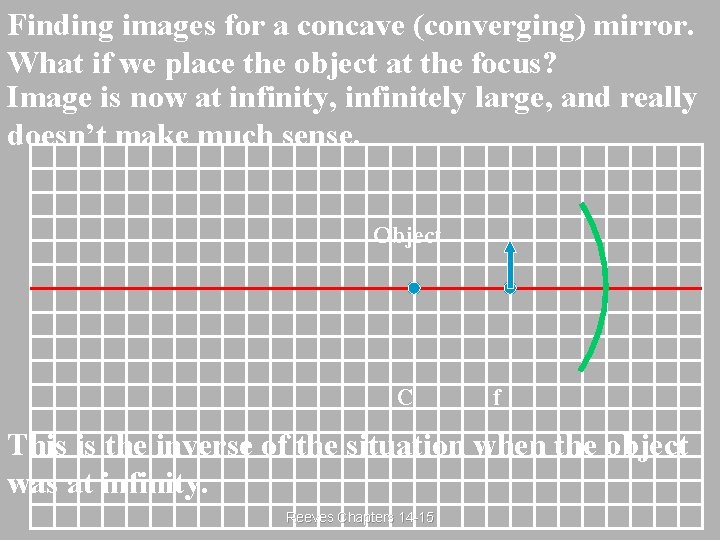
Finding images for a concave (converging) mirror. What if we place the object at the focus? Image is now at infinity, infinitely large, and really doesn’t make much sense. Object C f This is the inverse of the situation when the object was at infinity. Reeves Chapters 14 -15

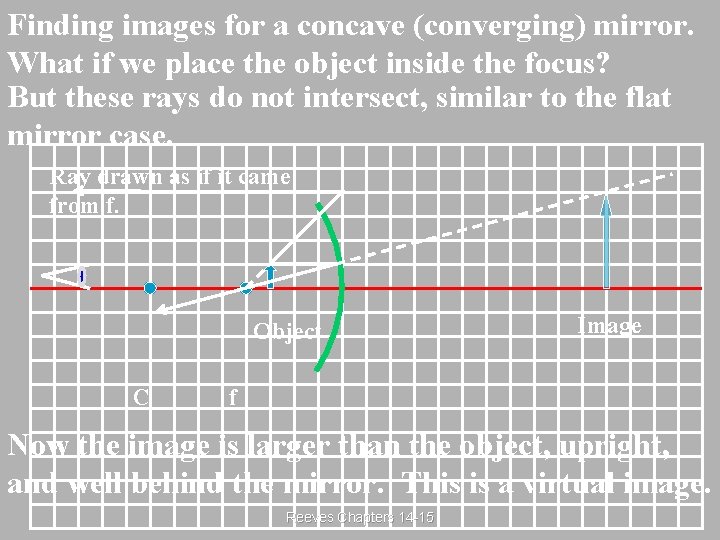
Finding images for a concave (converging) mirror. What if we place the object inside the focus? But these rays do not intersect, similar to the flat mirror case. Ray drawn as if it came from f. Object C Image f Now the image is larger than the object, upright, and well behind the mirror. This is a virtual image. Reeves Chapters 14 -15

Finding images for a concave (converging) mirror. Last time, very close to the mirror. This is getting very much like the flat mirror case. Object C Image f Now the image is slightly larger than the object, upright, and nearly the same distance behind the Reeves Chapters 14 -15 mirror. This is a virtual image.

Mirror Equations: (look familiar? !) § Image location § Magnification Minus signs are important! Reeves Chapters 14 -15

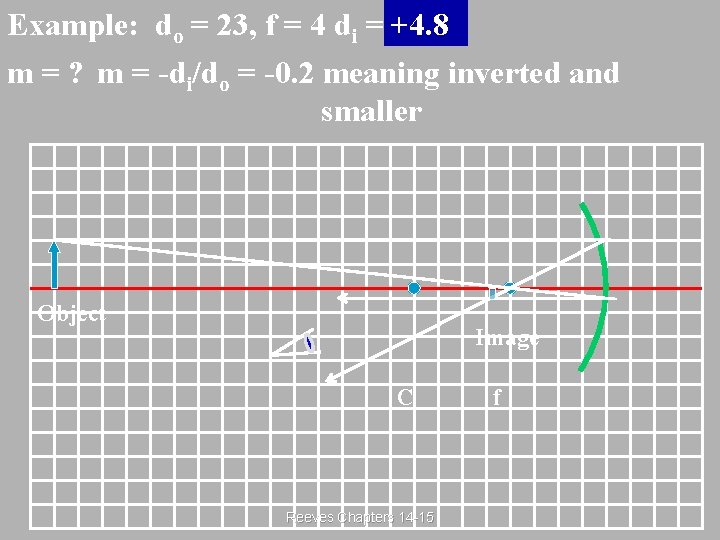
Example: do = 23, f = 4 di = +4. 8 ? m = -di/do = -0. 2 meaning inverted and smaller Object Image C Reeves Chapters 14 -15 f

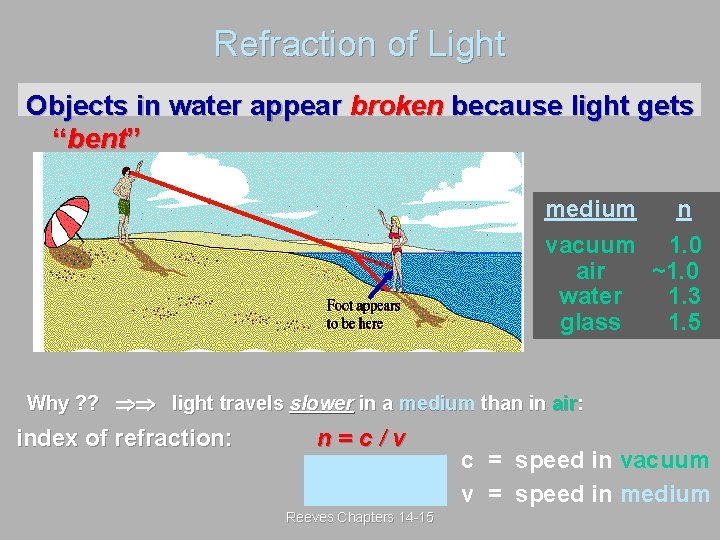
Refraction of Light Objects in water appear broken because light gets “bent” medium n vacuum 1. 0 air ~1. 0 water 1. 3 glass 1. 5 Why ? ? light travels slower in a medium than in air: index of refraction: n=c/v Reeves Chapters 14 -15 c = speed in vacuum v = speed in medium

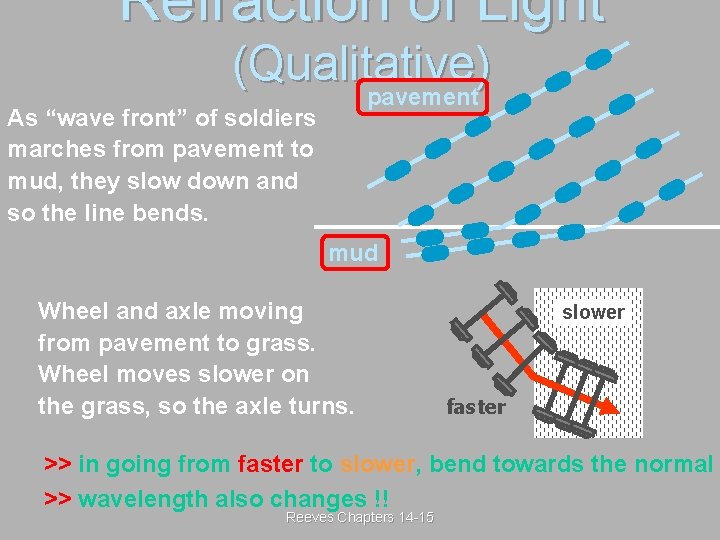
Refraction of Light (Qualitative) pavement As “wave front” of soldiers marches from pavement to mud, they slow down and so the line bends. mud Wheel and axle moving from pavement to grass. Wheel moves slower on the grass, so the axle turns. slower faster >> in going from faster to slower, bend towards the normal >> wavelength also changes !! Reeves Chapters 14 -15

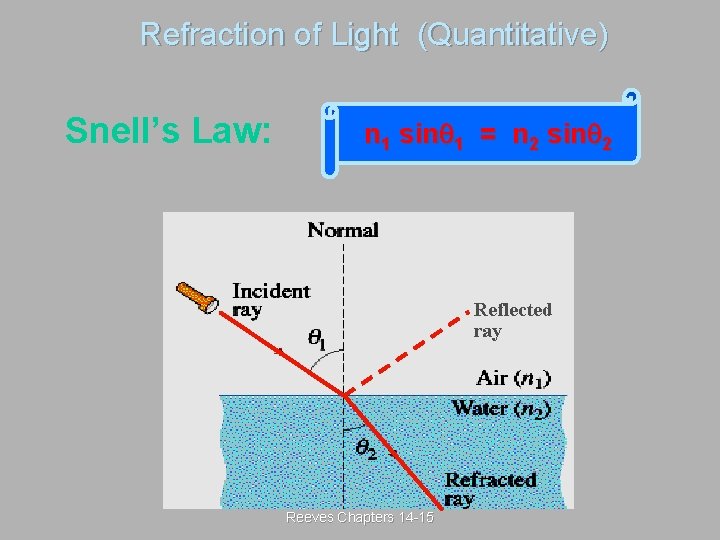
Refraction of Light (Quantitative) Snell’s Law: n 1 sin 1 = n 2 sin 2 Reflected ray Reeves Chapters 14 -15

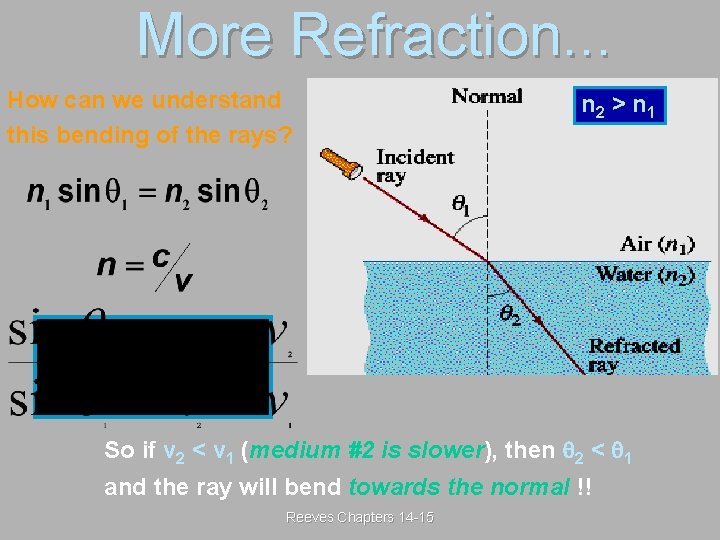
More Refraction. . . How can we understand this bending of the rays? n 2 > n 1 So if v 2 < v 1 (medium #2 is slower), then 2 < 1 and the ray will bend towards the normal !! Reeves Chapters 14 -15

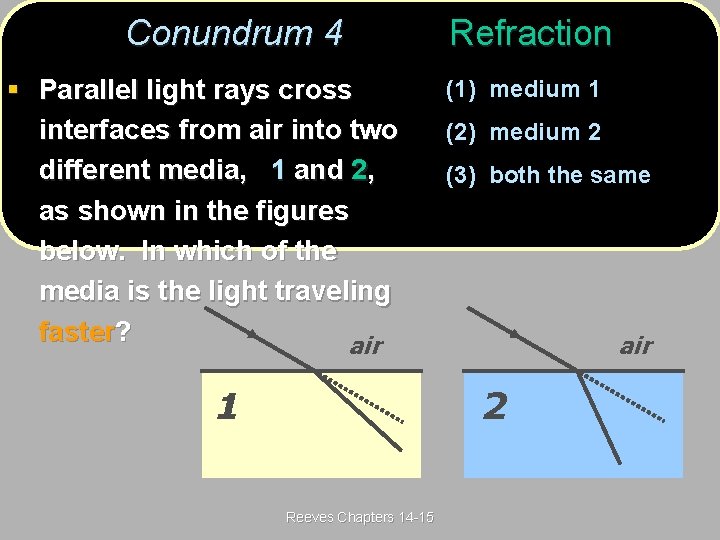
Conundrum 4(Post) Refraction 4 § Parallel light rays cross interfaces from air into two different media, 1 and 2, as shown in the figures below. In which of the media is the light traveling faster? air 1 (1) medium 1 (2) medium 2 (3) both the same air 2 Reeves Chapters 14 -15

Conundrum 4(Ans) Refraction 4 § Parallel light rays cross (1) medium 1 interfaces from air into two (2) medium 2 different media, 1 and 2, (3) both the same as shown in the figures below. In which of the media is the light traveling How does the speed in air faster? compare to that in 1 or 2 ? The greater the difference in the speed air of light between the two media, the greater the bending of the light rays. 1 Reeves Chapters 14 -15 air 2

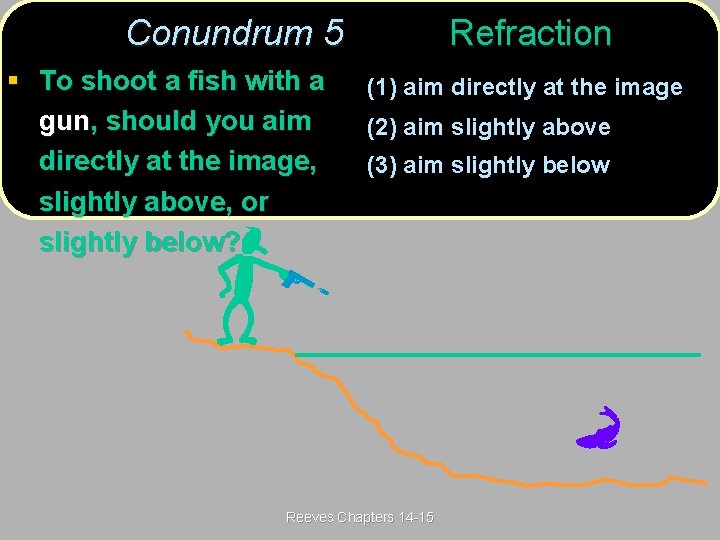
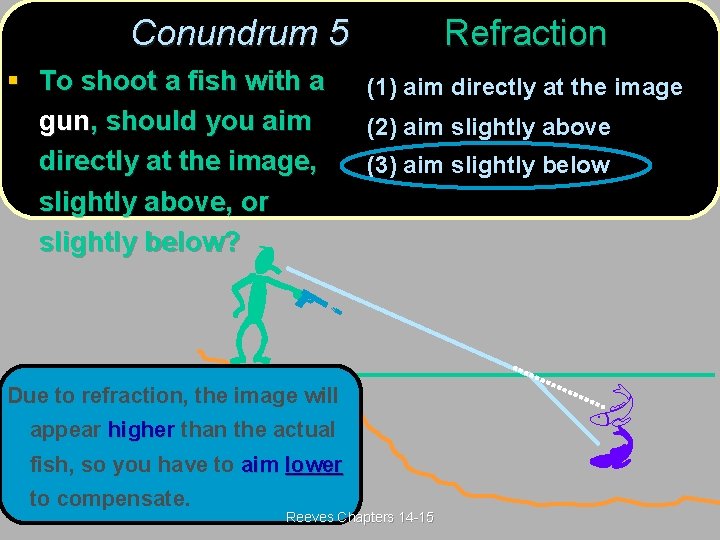
Conundrum 5(Post) Refraction 5 § To shoot a fish with a gun, should you aim directly at the image, slightly above, or slightly below? (1) aim directly at the image (2) aim slightly above (3) aim slightly below Reeves Chapters 14 -15

Conundrum 5(Ans) Refraction 5 § To shoot a fish with a gun, should you aim directly at the image, slightly above, or slightly below? (1) aim directly at the image (2) aim slightly above (3) aim slightly below Due to refraction, the image will appear higher than the actual fish, so you have to aim lower to compensate. Reeves Chapters 14 -15

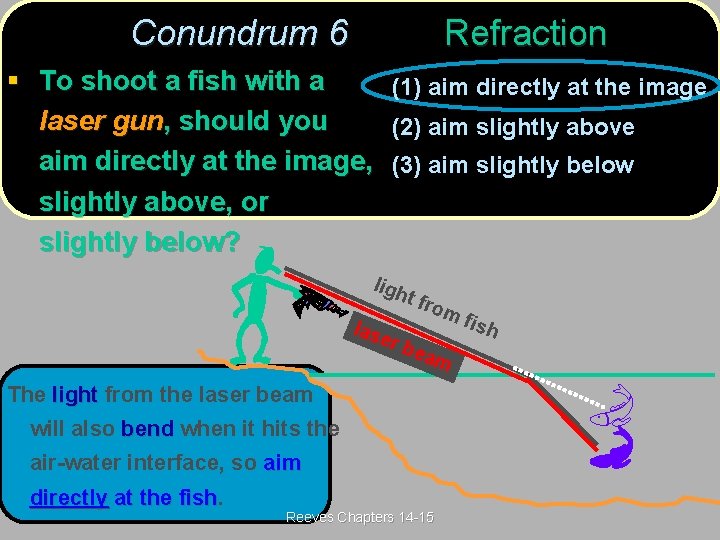
Conundrum 6(Post) Refraction 6 § To shoot a fish with a (1) aim directly at the image laser gun, should you (2) aim slightly above aim directly at the image, (3) aim slightly below slightly above, or slightly below? Reeves Chapters 14 -15

Conundrum 6(Ans) Refraction 6 § To shoot a fish with a (1) aim directly at the image laser gun, should you (2) aim slightly above aim directly at the image, (3) aim slightly below slightly above, or slightly below? ligh las t fro mf er b eam The light from the laser beam will also bend when it hits the air-water interface, so aim directly at the fish Reeves Chapters 14 -15 ish

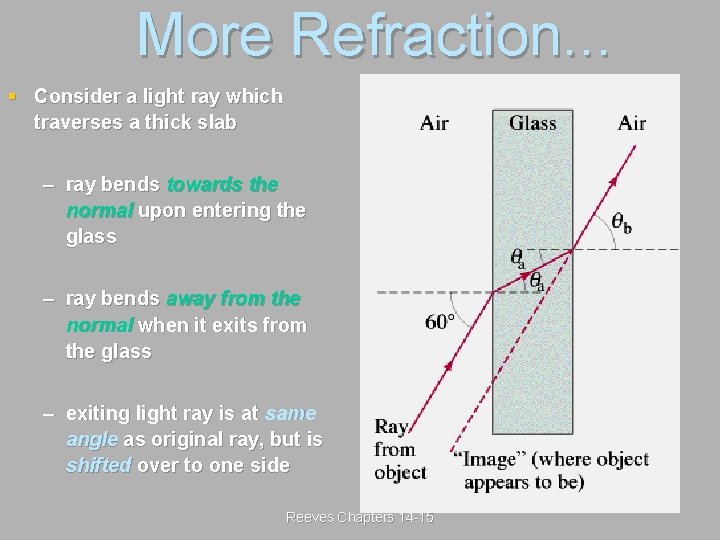
More Refraction. . . § Consider a light ray which traverses a thick slab – ray bends towards the normal upon entering the glass – ray bends away from the normal when it exits from the glass – exiting light ray is at same angle as original ray, but is shifted over to one side Reeves Chapters 14 -15

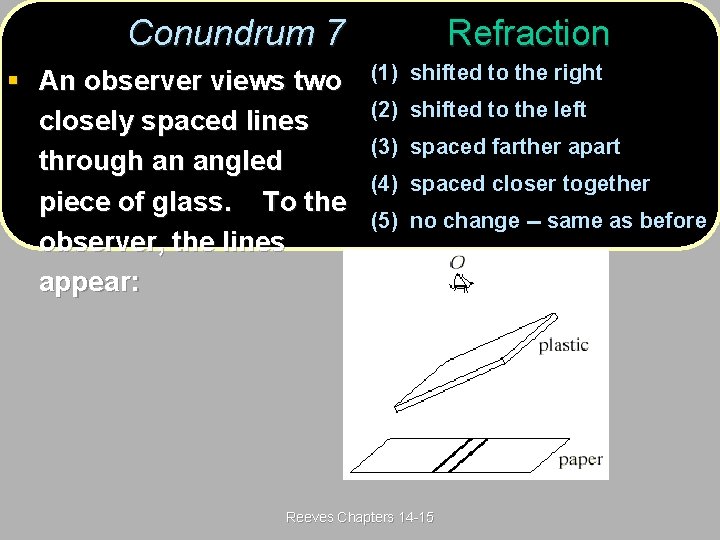
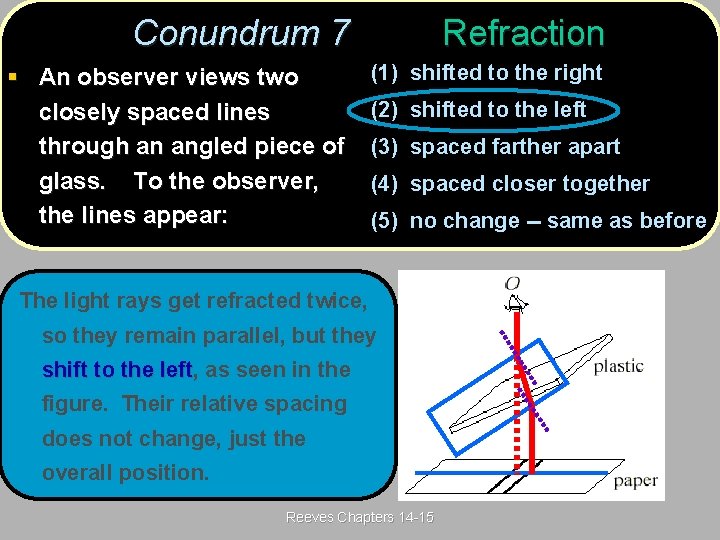
Conundrum 7(post) Refraction 7 § An observer views two closely spaced lines through an angled piece of glass. To the observer, the lines appear: (1) shifted to the right (2) shifted to the left (3) spaced farther apart (4) spaced closer together (5) no change -- same as before Reeves Chapters 14 -15

Conundrum 7(ans) Refraction 7 § An observer views two closely spaced lines through an angled piece of glass. To the observer, the lines appear: (1) shifted to the right (2) shifted to the left (3) spaced farther apart (4) spaced closer together (5) no change -- same as before The light rays get refracted twice, so they remain parallel, but they shift to the left, left as seen in the figure. Their relative spacing does not change, just the overall position. Reeves Chapters 14 -15

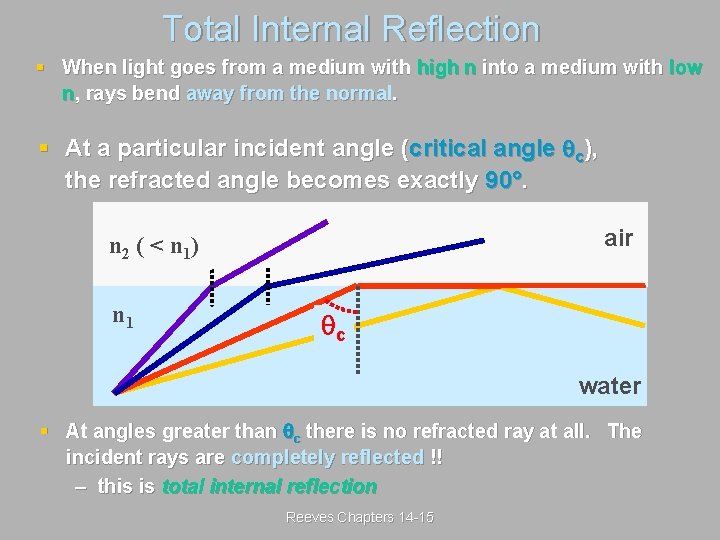
Total Internal Reflection § When light goes from a medium with high n into a medium with low n, rays bend away from the normal. § At a particular incident angle (critical angle c), the refracted angle becomes exactly 90°. air n 2 ( < n 1) n 1 c water § At angles greater than c there is no refracted ray at all. The incident rays are completely reflected !! – this is total internal reflection Reeves Chapters 14 -15

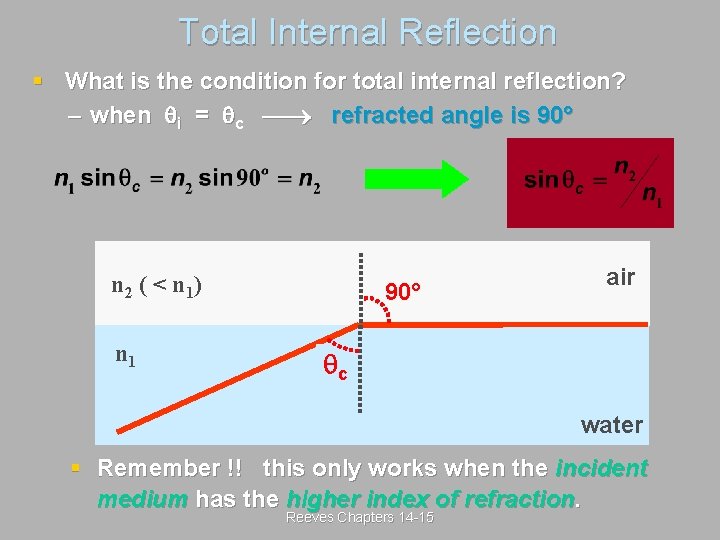
Total Internal Reflection § What is the condition for total internal reflection? – when i = c refracted angle is 90° n 2 ( < n 1) n 1 90° air c water § Remember !! this only works when the incident medium has the higher index of refraction. Reeves Chapters 14 -15

Refraction § A beam of light is emitted in a pool of water from a depth of 62 cm. How far away must it strike the air-water surface, relative to the spot directly above it, so that the light does not exit the water? See Problem 23 -42 Reeves Chapters 14 -15

The Visible Spectrum § Remember that white light contains all the colors of the spectrum – recall the separation of colors from Reeves Chapters 14 -15

Diffraction grating with different colors § If the light has two wavelengths, we get two sets of maxima: § If it is white light (all colors, therefore all wavelengths): Reeves Chapters 14 -15

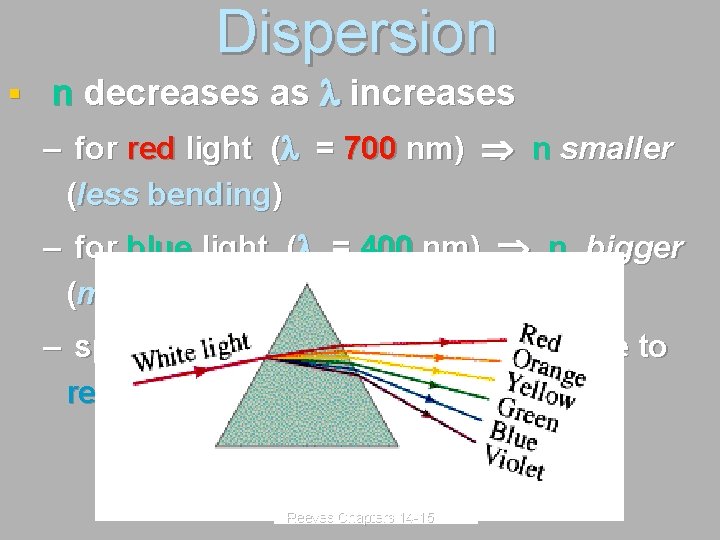
Dispersion § n decreases as l increases – for red light (l = 700 nm) n smaller (less bending) – for blue light (l = 400 nm) n bigger (more bending) – spreading (dispersion) of colors due to refraction !! Reeves Chapters 14 -15

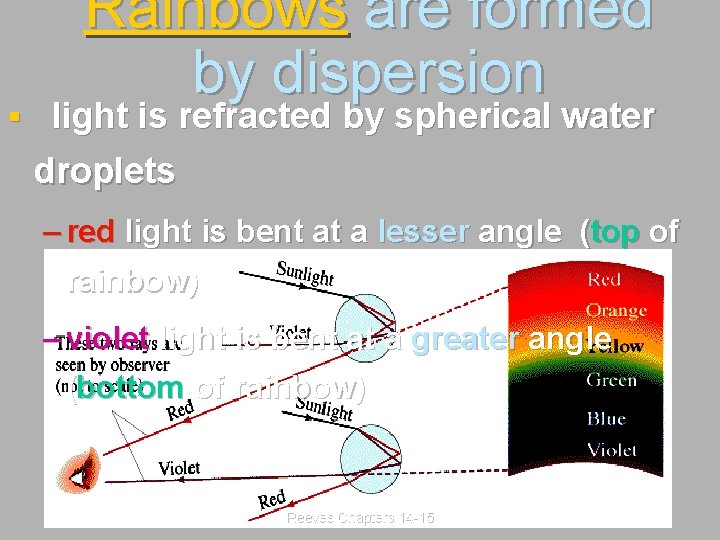
Rainbows are formed by dispersion § light is refracted by spherical water droplets – red light is bent at a lesser angle (top of rainbow) – violet light is bent at a greater angle (bottom of rainbow) Reeves Chapters 14 -15