Reflection MCC 8 G 3 Describe the effect

Reflection MCC 8. G. 3 Describe the effect of dilations, translations, rotations and reflections on two-dimensional figures using coordinates.

• One type of transformation uses a line that acts like a mirror, with an image reflected across a line is a reflection and the mirror line is the line of reflection.

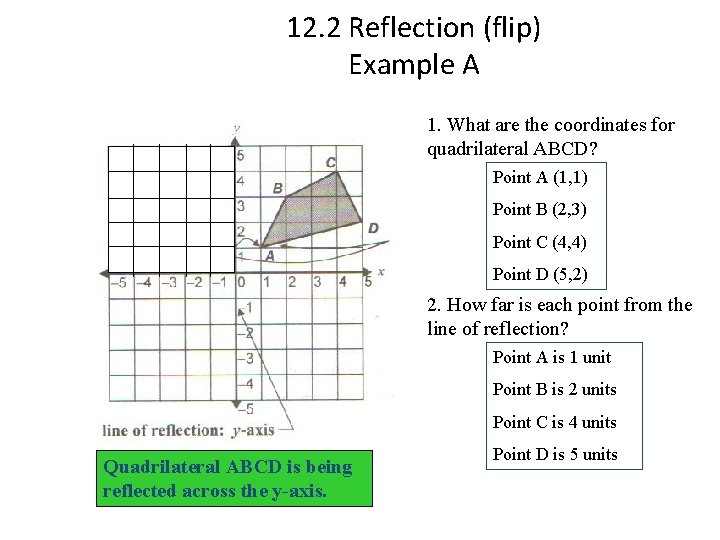
12. 2 Reflection (flip) Example A 1. What are the coordinates for quadrilateral ABCD? Point A (1, 1) Point B (2, 3) Point C (4, 4) Point D (5, 2) 2. How far is each point from the line of reflection? Point A is 1 unit Point B is 2 units Point C is 4 units Quadrilateral ABCD is being reflected across the y-axis. Point D is 5 units

12. 2 Reflection (flip) Example A 3. Using the information in question 2, how far should the image be from the line of reflection? Pre-image Image Point A is 1 unit Point A′ is 1 unit Point B is 2 units Point B′ is 2 units Point C is 4 units Point C′ is 4 units Point D is 5 units Point D′ is 5 units REMEMBER: Each vertex should be the same distance from the line of symmetry, just in the opposite position.

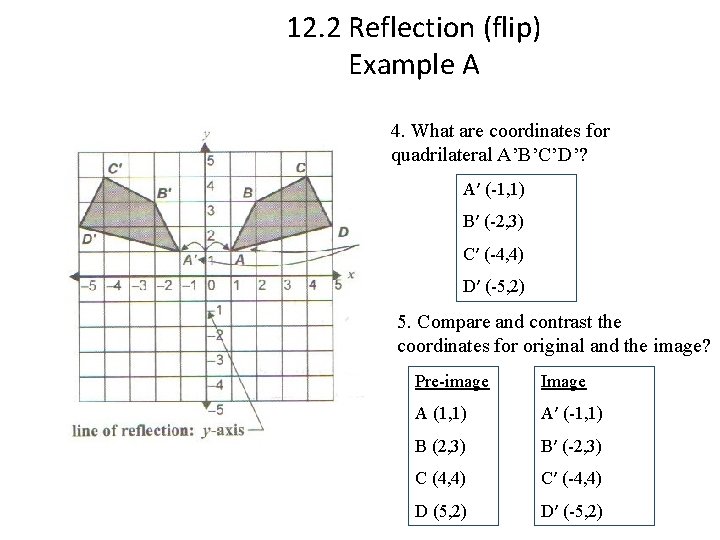
12. 2 Reflection (flip) Example A 4. What are coordinates for quadrilateral A’B’C’D’? A′ (-1, 1) B′ (-2, 3) C′ (-4, 4) D′ (-5, 2) 5. Compare and contrast the coordinates for original and the image? Pre-image Image A (1, 1) A′ (-1, 1) B (2, 3) B′ (-2, 3) C (4, 4) C′ (-4, 4) D (5, 2) D′ (-5, 2)

12. 2 Reflection (flip) Example B Write down the coordinates for the original and the image. Compare and contrast the coordinates? This time the original is being reflected over the x-axis. Pre-Image F (2, 3) F′ (2, -3) G (4, 1) G′ (4, -1) H (1, 0) H′ (1, 0)

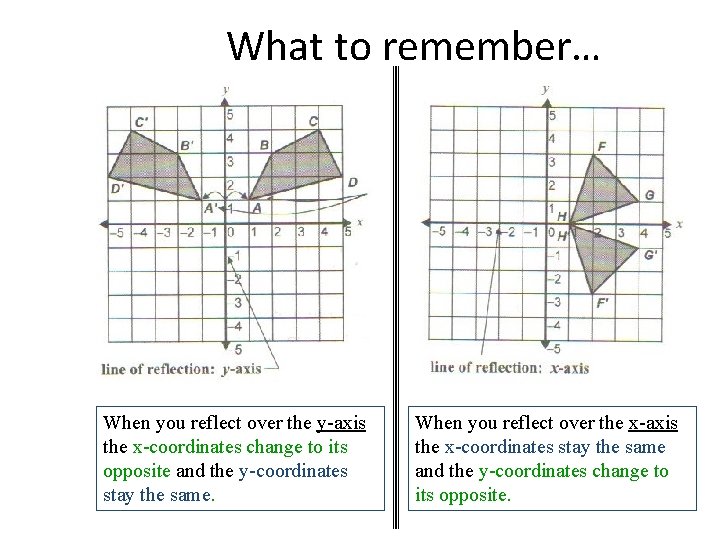
What to remember… When you reflect over the y-axis the x-coordinates change to its opposite and the y-coordinates stay the same. When you reflect over the x-axis the x-coordinates stay the same and the y-coordinates change to its opposite.

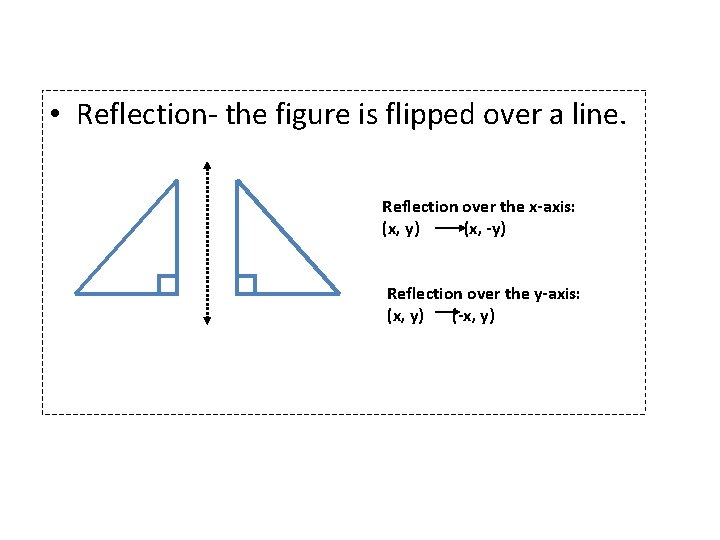
• Reflection- the figure is flipped over a line. Reflection over the x-axis: (x, y) (x, -y) Reflection over the y-axis: (x, y) (-x, y)

What happens if the line of reflection is not the axis?

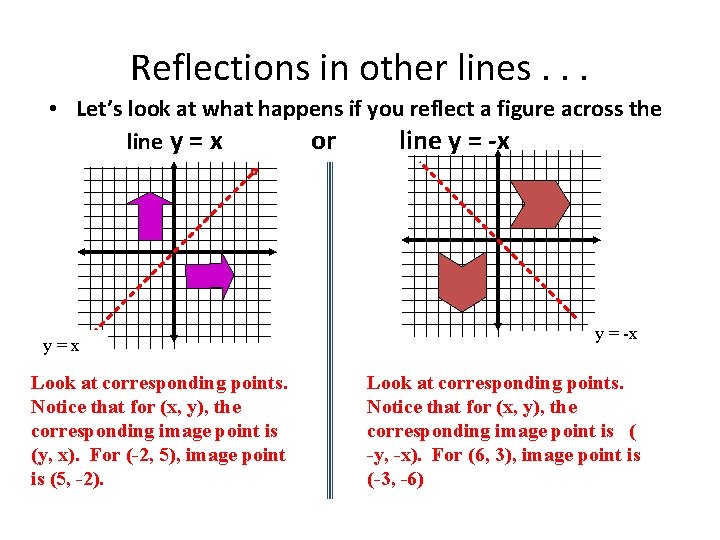
Reflections in other lines. . . • Let’s look at what happens if you reflect a figure across the line y = x or line y = -x y=x Look at corresponding points. Notice that for (x, y), the corresponding image point is (y, x). For (-2, 5), image point is (5, -2). y = -x Look at corresponding points. Notice that for (x, y), the corresponding image point is ( -y, -x). For (6, 3), image point is (-3, -6)

What does y=a look like? • a represents any number. Let’s graph y = 3 y=3 x -2 1 4 y 3 3 3 What type of line did you graph? Horizontal line (x, y) (-2, 3) (1, 3) (4, 3)

What does x=c look like? • c represents any number. Let’s graph x = -2 x -2 -2 -2 y 5 0 -3 What type of line did you graph? Vertical line (x, y) (-2, 5) (-2, 0) (-2, -3)

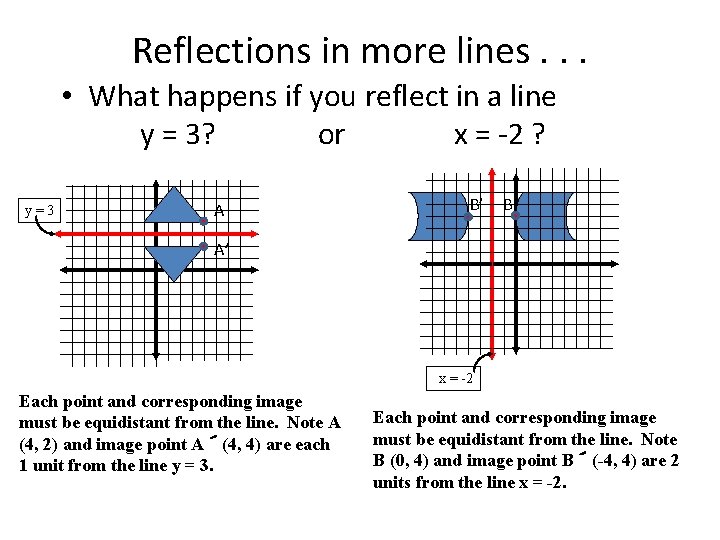
Reflections in more lines. . . • What happens if you reflect in a line y = 3? or x = -2 ? y=3 A B’ B A’ x = -2 Each point and corresponding image must be equidistant from the line. Note A (4, 2) and image point A′(4, 4) are each 1 unit from the line y = 3. Each point and corresponding image must be equidistant from the line. Note B (0, 4) and image point B′(-4, 4) are 2 units from the line x = -2.

Steps to finding the image coordinates 1. Determine if the figure will reflect horizontally or vertically. This will tell you which coordinate will change. Since it Y=3 only the y-coordinate will change. 2. Find the distance between the pre-image coordinate and the line of reflection by subtracting the coordinate from the value of the line. U (-3, 5) 5– 3=2 U is 2 units above y=3 So how far should U′ be the line of reflection? 2 units below

Steps to finding the image coordinates 3. Since it should be below, subtract the distance from the value of the line of reflection. U (-3, 5) U′ should be 2 units below Line of reflection y=3 3 -2 = 1 So U′ should be at (-3, 1) 4. Check by graphing

Reteach Video next

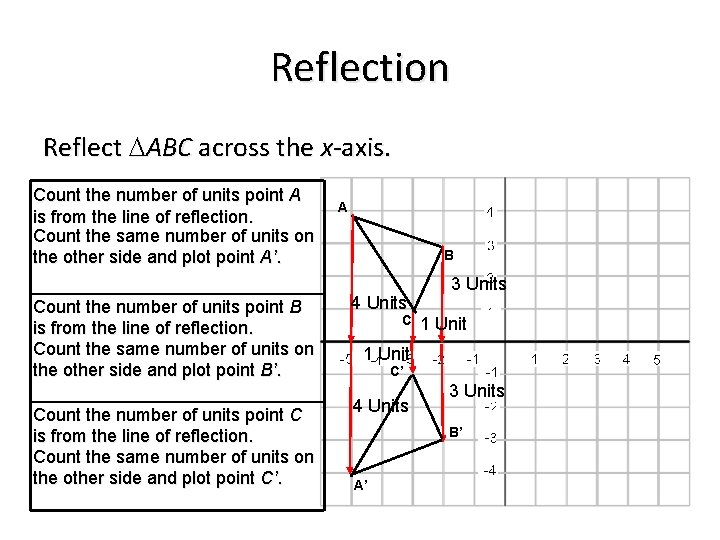
Reflection Reflect ABC across the x-axis. Count the number of units point A is from the line of reflection. Count the same number of units on the other side and plot point A’. A B Count the number of units point B is from the line of reflection. Count the same number of units on the other side and plot point B’. 4 Units Count the number of units point C is from the line of reflection. Count the same number of units on the other side and plot point C’. 4 Units C 3 Units 1 Unit C’ 3 Units B’ A’

Reflections in a line • Reflections can be made across the x-axis Look at the corresponding points in the figures. The point (-4, 4) corresponds to the image point (-4, -4). The point (2, 4) corresponds to (2, -4). Notice that in a reflection over the x-axis, the coordinates of the x’s stay the same but the y’s change sign. In a reflection across the x-axis, the point (x, y) reflects onto image (x, -y).

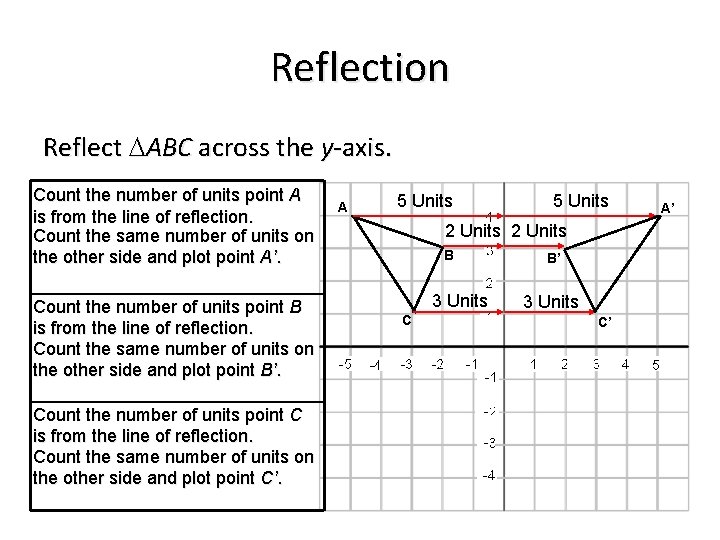
Reflection Reflect ABC across the y-axis. Count the number of units point A is from the line of reflection. Count the same number of units on the other side and plot point A’. Count the number of units point B is from the line of reflection. Count the same number of units on the other side and plot point B’. Count the number of units point C is from the line of reflection. Count the same number of units on the other side and plot point C’. A 5 Units 2 Units B 3 Units C B’ 3 Units C’ A’

Reflections in the y axis • Reflections can be made across the y-axis Check the corresponding points here. Notice that the point (2, 1) corresponds to (-2, 1). The point (7, 1) corresponds to (-7, 1). The y values stay the same, but the x values change sign. In a reflection across the y axis, the point (x, y) reflects onto image (-x, y).