Reflecting Points on the Coordinate Plane Review of

Reflecting Points on the Coordinate Plane

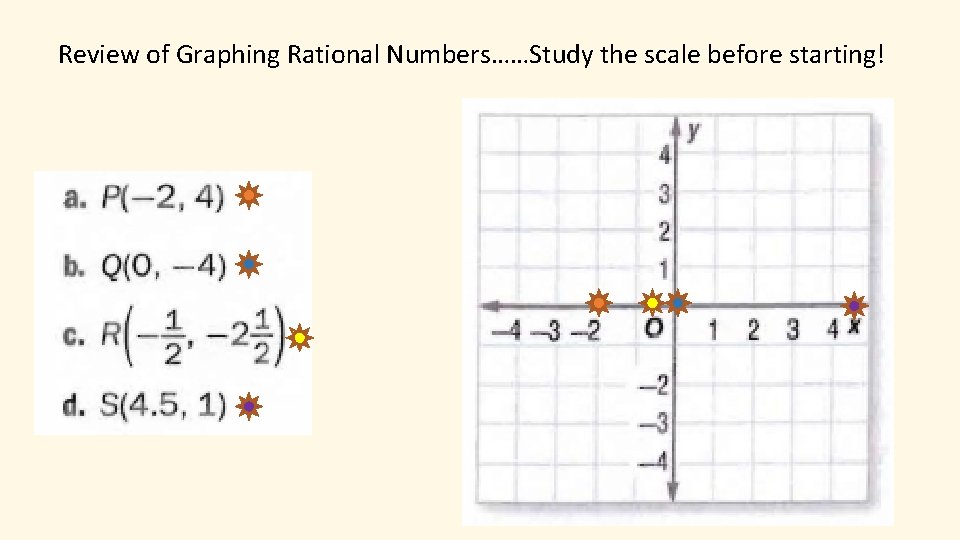
Review of Graphing Rational Numbers……Study the scale before starting!

Reflections • The vocabulary associated with reflections • What they look like • Graphing reflections • Finding the rule

In mathematics, a transformation of an object changes the position or orientation of a figure. There are three types of transformations: translations, rotations, and reflections. The resulting figure is the image of the original. A reflection creates a mirror image of an object or point. The orientation of the object or point is also reversed, creating a mirror image. The line across which the image is reflected is called the line of reflection.

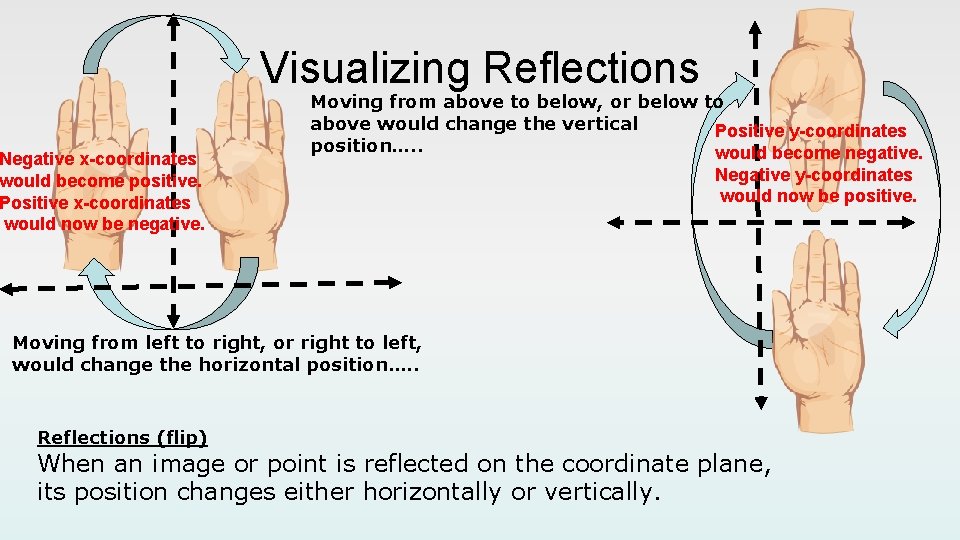
Visualizing Reflections Negative x-coordinates would become positive. Positive x-coordinates would now be negative. Moving from above to below, or below to above would change the vertical Positive y-coordinates position…. . would become negative. Negative y-coordinates would now be positive. Moving from left to right, or right to left, would change the horizontal position…. . Reflections (flip) When an image or point is reflected on the coordinate plane, its position changes either horizontally or vertically.

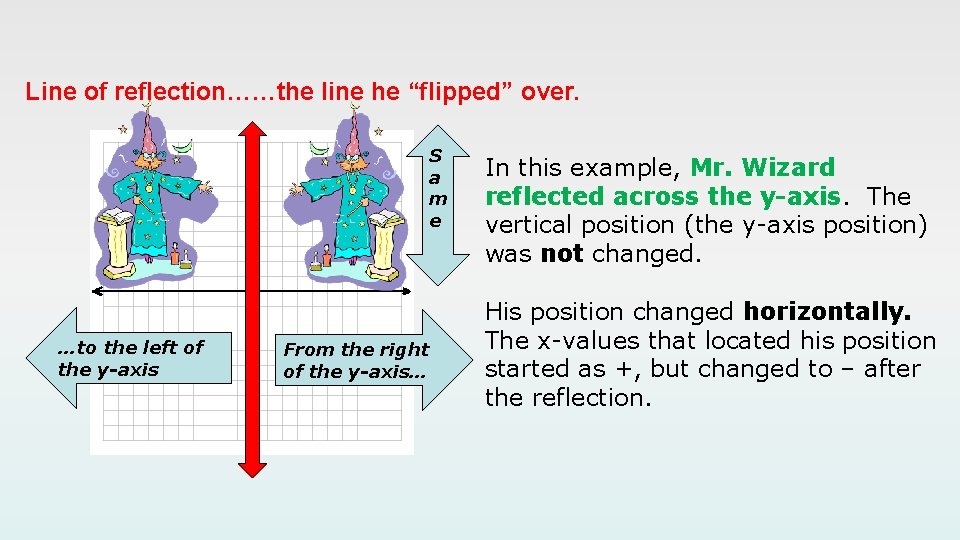
Line of reflection……the line he “flipped” over. S a m e …to the left of the y-axis From the right of the y-axis… In this example, Mr. Wizard reflected across the y-axis. The vertical position (the y-axis position) was not changed. His position changed horizontally. The x-values that located his position started as +, but changed to – after the reflection.

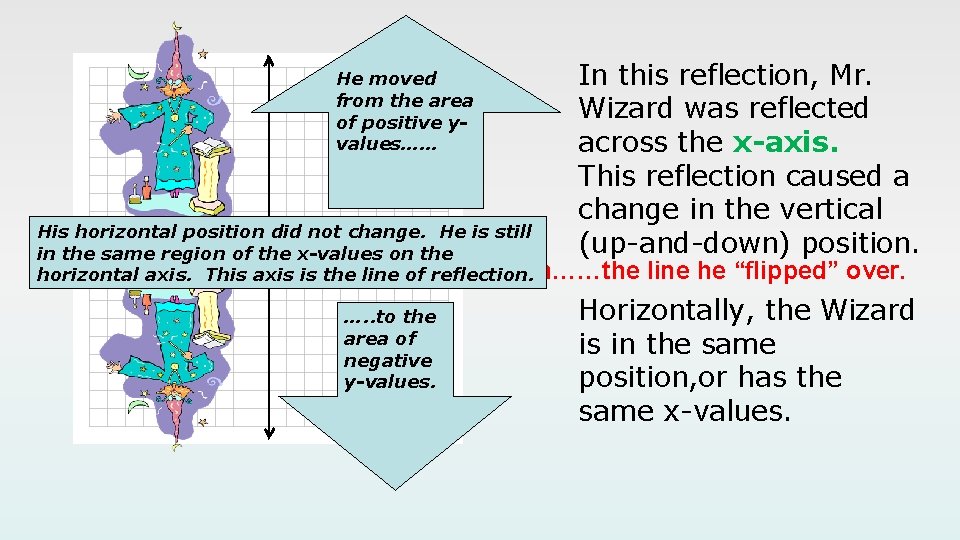
He moved from the area of positive yvalues…… In this reflection, Mr. Wizard was reflected across the x-axis. This reflection caused a change in the vertical (up-and-down) position. His horizontal position did not change. He is still in the same region of the x-values on the ofreflection……the horizontal axis. This axis is the. Line line of …. . to the area of negative y-values. line he “flipped” over. Horizontally, the Wizard is in the same position, or has the same x-values.

When you reflect a point, you have to have a way to separate the original point from the image point. You use a prime notation. A’ is called A prime.

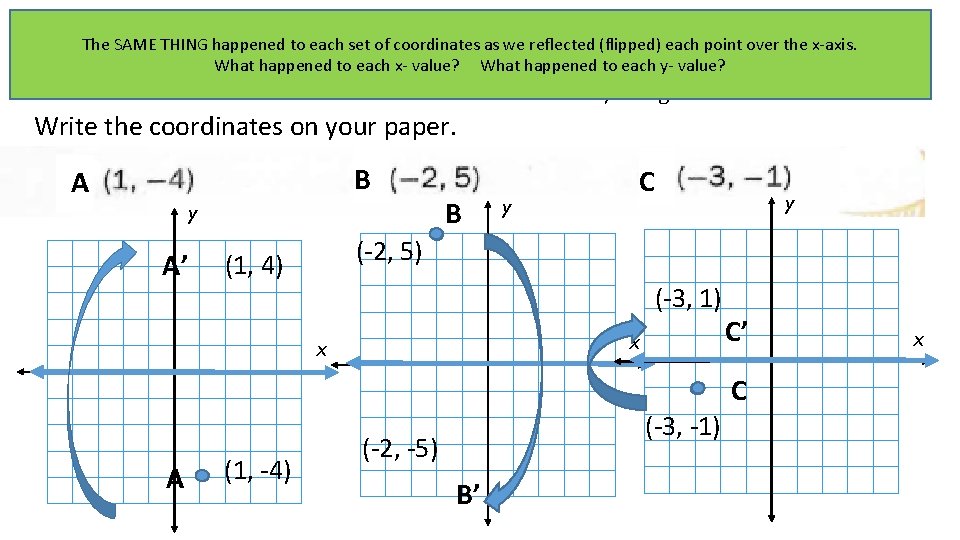
The SAME THING happened to each set of coordinates as we reflected (flipped) each point over the x-axis. We will reflect each point across x-axis. What happened to each y- value? What happened to eachthe x- value? We will name the new location, using the correct notation. Write the coordinates on your paper. B A y A’ B (1, -4) y (-2, 5) (1, 4) (-3, 1) x x A y C (-3, -1) (-2, -5) B’ C’ C x

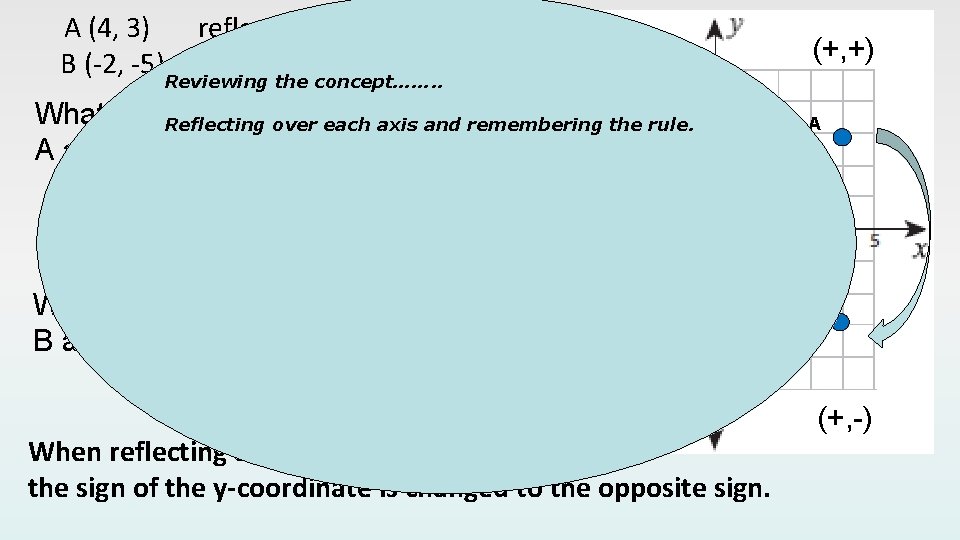
A (4, 3) reflect across the x-axis B (-2, -5)Reviewing reflectthe across the x-axis concept……. . (-, +) B’ What is the distance Reflecting overbetween each axis and remembering the rule. A and A’? A’ ( 4, -3 ) (+, +) A B’ ( -2, 5 ) What is the distance between B and B’? A’ (-, -) B When reflecting across the x-axis the sign of the y-coordinate is changed to the opposite sign. (+, -)

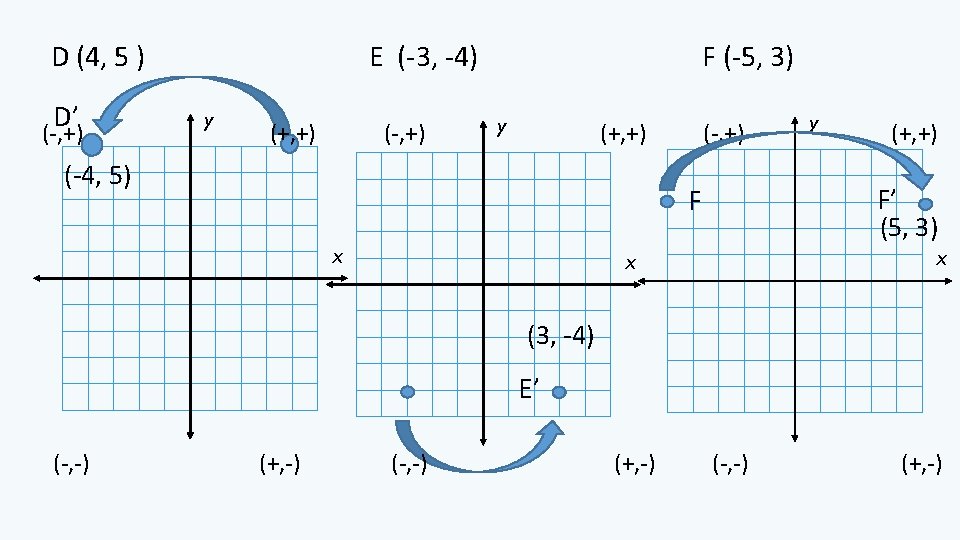
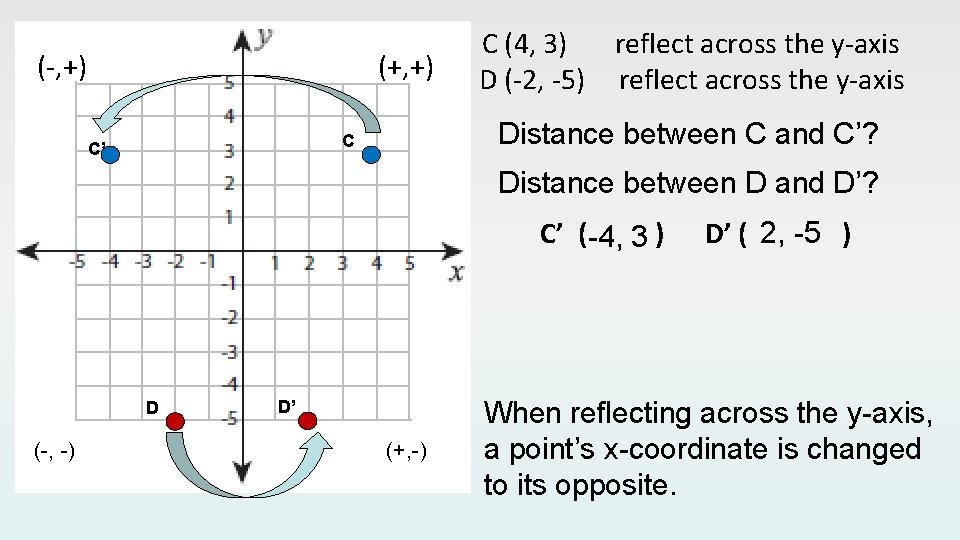
(-, +) (+, +) Distance between C and C’? C C’ C (4, 3) reflect across the y-axis D (-2, -5) reflect across the y-axis Distance between D and D’? C’ ( -4, 3 ) D (-, -) D’ (+, -) D’ ( 2, -5 ) When reflecting across the y-axis, a point’s x-coordinate is changed to its opposite.

What did we accomplish? • We reflected points on the coordinate plane. • We named the new location using prime notation. • We found a rule that applies to all reflections. • Video: • https: //www. youtube. com/watch? v=q. C 9_wj. LVo. P 4

Practice IXL. com • X. Coordinate plane • 1 Objects on a coordinate plane • 2 Graph points on a coordinate plane • 3 Quadrants • 4 Coordinate planes as maps • 5 Distance between two points • 6 Follow directions on a coordinate plane • DD. Symmetry and transformations • 8 Reflections: graph the image