REFLECTED IMPEDANCE POWER EQUIVALENT RESISTANCE REACTANCE PHASOR DIAGRAM











- Slides: 13

REFLECTED IMPEDANCE & POWER EQUIVALENT RESISTANCE, REACTANCE & PHASOR DIAGRAM OF TRANSFORMER Lecture No. 11 By. Sajid Hussain Qazi

REFLECTED IMPEDANCE In the previous section we found that, Dividing the first by the second, we have

REFLECTED IMPEDANCE However, since Then, Equation 1 The above equation states that the impedance of the primary circuit of an ideal transformer is the transformation ratio squared times the impedance of the load.

REFLECTED IMPEDANCE If a transformer is used, therefore, an impedance can be made to appear larger or smaller at the primary by placing it in the secondary of a step-down (a > 1) or step-up (a < 1) transformer, respectively. Note that if the load is capacitive or inductive, the reflected impedance will also be capacitive or inductive.

Power of Transformer For the ideal iron-core transformer,

Example: For the iron-core transformer of Figure shown a. Find the magnitude of the current in the primary and the impressed voltage across the primary. b. Find the input resistance of the transformer.

Example: -

EQUIVALENT RESISTANCE, REACTANCE If we now reflect the secondary circuit through the ideal transformer using Eq. (1), as shown in Figure below, we will have the load and generator voltage in the same continuous circuit.

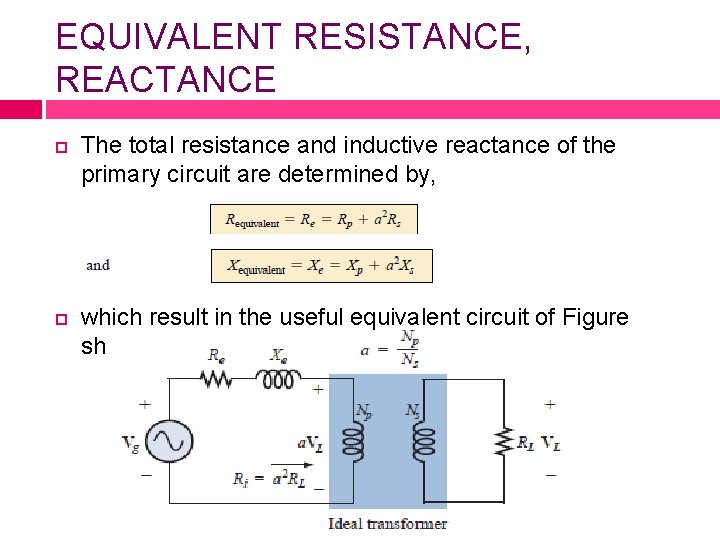
EQUIVALENT RESISTANCE, REACTANCE The total resistance and inductive reactance of the primary circuit are determined by, which result in the useful equivalent circuit of Figure shown.

EQUIVALENT RESISTANCE, REACTANCE The load voltage can be obtained directly from the circuit of Figure shown above through the voltage divider rule: Equation 2

Phasor Diagram of Transformer The figure shown above will also allow us to calculate the generator voltage necessary to establish a particular load voltage. The voltages across the elements of above figure have the phasor relationship indicated in Figure below. . .

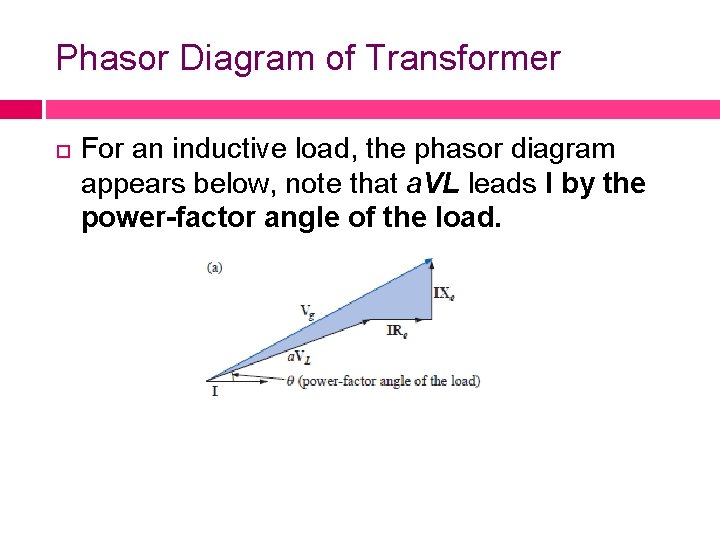
Phasor Diagram of Transformer For an inductive load, the phasor diagram appears below, note that a. VL leads I by the power-factor angle of the load.

Phasor Diagram of Transformer The effect of Re and Xe on the magnitude of Vg for a particular VL is obvious from Eq. (2). For increased values of Re or Xe, an increase in Vg is required for the same load voltage. For Re and Xe=0, VL and Vg are simply related by the turns ratio.