Refining Rules Incorporated into KnowledgeBased Support Vector Learners

Refining Rules Incorporated into Knowledge-Based Support Vector Learners via Successive Linear Programming Richard Maclin University of Minnesota - Duluth Edward Wild, Jude Shavlik, Lisa Torrey, Trevor Walker University of Wisconsin - Madison

The Setting Given • Examples for classification/regression task • Advice from an expert about the task Do • Learn an accurate model • Refine the advice (if needed) Knowledge-Based Support Vector Classification/Regression

Motivation • Advice-taking methods incorporate human user’s knowledge • But users may not be able to precisely define advice • Idea: allow users to specify advice but refine the advice with the data

An Example of Advice True concept IF (3 x 1 – 4 x 2) > -1 THEN class = + ELSE class = Examples 0. 8 , 0. 7 , 0. 3 , 0. 2 , + 0. 2 , 0. 6 , 0. 8 , 0. 1 , Advice IF (3 x 1 – 4 x 2) > 0 THEN class = + ELSE class = (wrong, threshold should be -1)

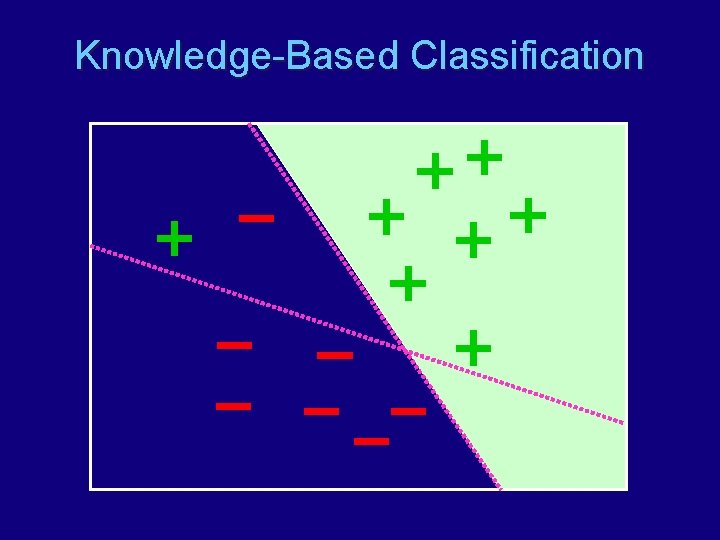
Knowledge-Based Classification

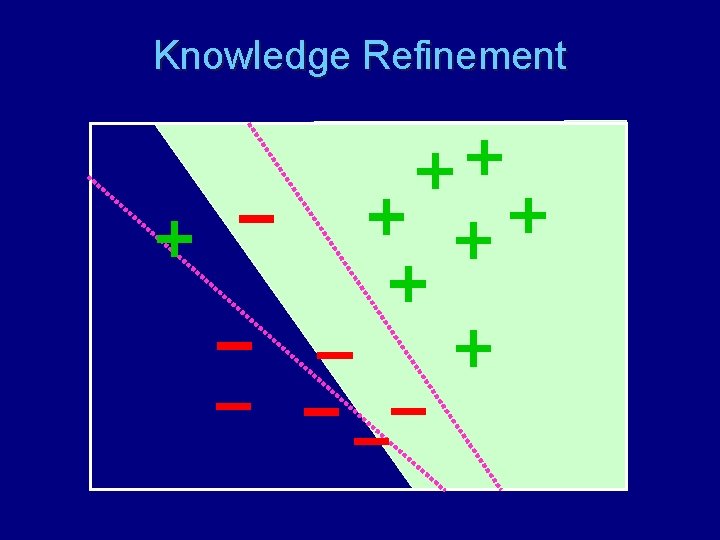
Knowledge Refinement

SVM Formulation min (model complexity) + C (penalties for error) such that model fits data (with slack vars for error)

Knowledge-Based SVMs [Fung et al. , 2002, 2003 (KBSVM), Mangasarian et al. , 2004 (KBKR)] min (model complexity) + C (penalties for error) + (µ 1, µ 2) (penalties for not following advice) such that model fits data (with slack vars for error) + model fits advice (also with slacks)

Refining Advice min (model complexity) + C (penalties for error) + (µ 1, µ 2) (penalties for not following advice) + ρ (penalties for changing advice) such that model fits data (with slack vars for error) + model fits advice (also with slacks) + variables to refine advice

Incorporating Advice in KBKR Advice format Bx ≤ d f(x) ≥ IF (3 x 1 – 4 x 2) > 0 THEN class = + (f(x) ≥ 1) f(x) ≥ 1

Linear Programming with Advice Bx ≤ d f(x) ≥ IF (3 x 1 – 4 x 2) > 0 THEN class = + KBSVMs: min ||w||1 + |b| + C||s||1 sum per advice k µ 1||zk||1+µ 2ζk such that Y(w. Tx +b) + s ≥ 1 for each advice k wk+Bk. Tuk = zk -d. Tuk + ζk ≥ βk – bk (s, uk, ζk)≥ 0

Refining Advice Bx ≤ (d - δ) f(x) ≥ KBSVMs: min ||w||1 + |b| + C||s||1 sum per advice k µ 1||zk||1+µ 2ζk+ρ||δ||1 such that Would like to just Tx +b) + s ≥ 1 Y(w add to linear for each advice k programming wk+Bk. Tuk = zk formulation, but (δ-d)Tuk + ζk ≥ βk – bk Cannot solve for δ and (s, uk, ζk)≥ 0 u simultaneously!

Solution: Successive Linear Programming Rule-Refining Support Vector Machines (RRSVM) algorithm: Set δ=0 Repeat Fix value of δ and solve LP for u Fix value of u and solve LP for δ Until no change to δ or max # of repeats

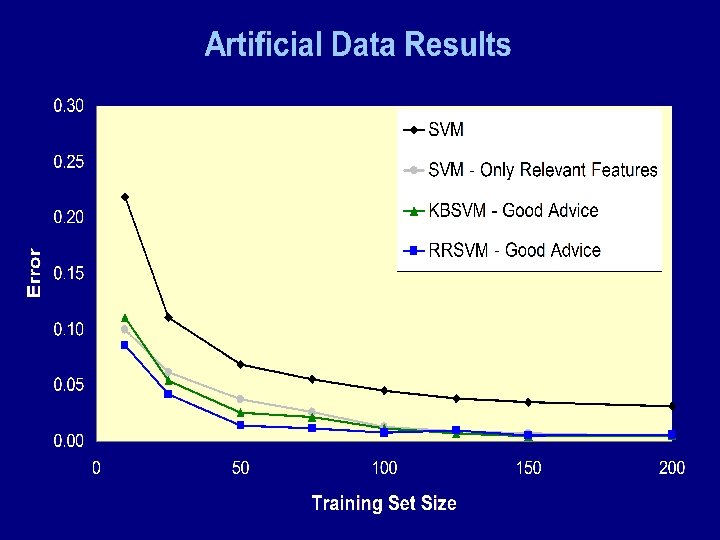
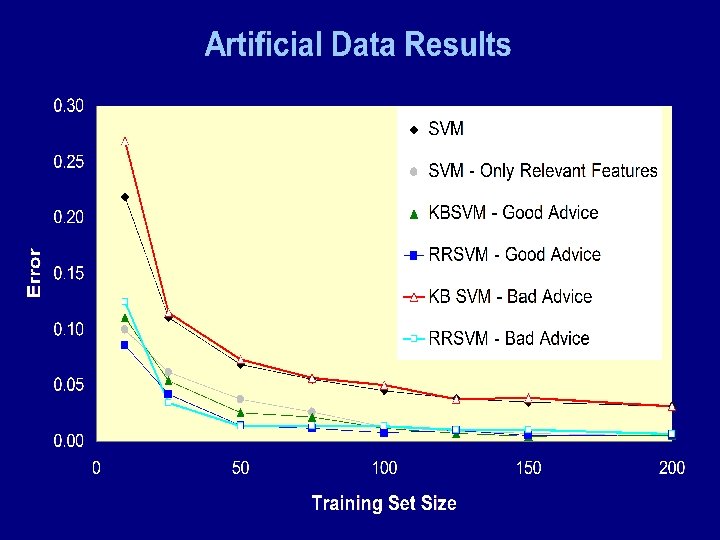
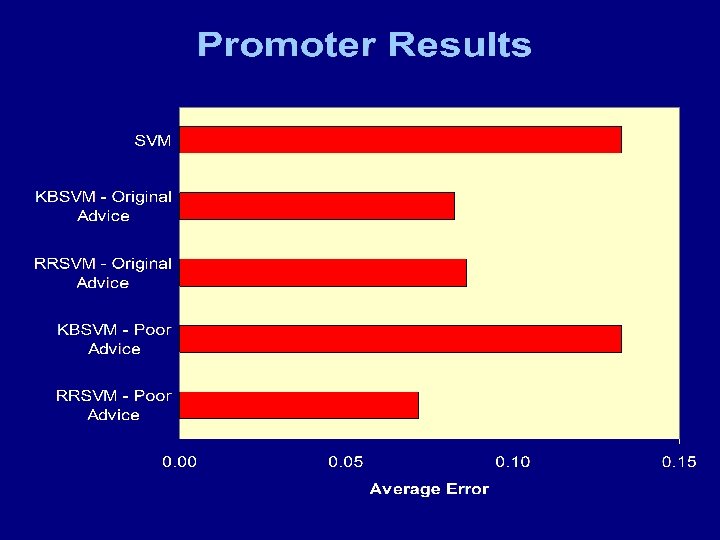
Experiments Artificial data sets IF (3 x 1– 4 x 2)>-1 THEN class = + ELSE class = - Data randomly generated (with and w/o noise) Errors added (e. g. , -1 dropped) to make advice Promoter data set Data: Towell et al. (1990) Domain theory: Ortega (1995)

Methodology • Experiments repeated twenty times • Artificial data results – training and test set randomly generated (separately) • Promoter data – ten fold cross validation • Parameters chosen using cross validation (ten folds) on training data Standard SVMs: KBSVMs: RRSVMs: C C, µ 1, µ 2 , ρ

Related Work • Knowledge-Based Kernel Methods – – – Fung et al. , NIPS 2002, COLT 2003 Mangasarian et al. , JMLR 2005 Maclin et al. , AAAI 2005, 2006 Le et al. , ICML 2006 Mangasarian and Wild, IEEE Trans Neural Nets 2006 • Knowledge Refinement – Towell et al. , AAAI 1990 – Pazzani and Kibler, MLJ 1992 – Ourston and Mooney, AIJ 1994 • Extracting Learned Knowledge from Networks – – Fu, AAAI 1991 Towell and Shavlik, MLJ 1993 Thrun, 1995 Fung et al. , KDD 2005

Future Work • Test on other domains • Address limitations (speed, # of parameters) • Refine multipliers of antecedents • Add additional terms to rules • Investigate rule extraction methods

Conclusions RRSVM • Key idea: refine advice by adjusting thresholds of rules • Can produce more accurate models • Able to produce changes to advice • Have shown that RRSVM converges

Acknowledgements • US Naval Research Laboratory grant N 00173 -06 -1 -G 002 (to RM) • DARPA grant HR 0011 -04 -1 -0007 (to JS)

Questions?