ReferenceBased Alignment in Large Sequence Databases Speaker Panagiotis

Reference-Based Alignment in Large Sequence Databases Speaker: Panagiotis Papapetrou Boston University Joint work with: Vassilis Athitsos (UTA) George Kollios (BU) Dimitrios Gunopulos (UOA and UCR) 1

General Problem Given: S: collection of strings. Q: query string. D: similarity measure. Find that substring of S that is most similar to Q, under the similarity measure D. 2

Motivation Spell-checking: Data cleaning: given some input text the spell-checker consults its dictionary to find words of high similarity to the text, so as to identify potential typos. data obtained from different sources might contain inconsistencies which can be eliminated by looking for similar entities (strings) in the data. Near homology search in biological sequences: given different genomes we want to find regions of high similarity that were the result of a mutation, etc. 3

Motivation Our focus: Near homology search in DNA sequences. Two major requirements: Retrieve near-exact matches of long query sequences efficiently. Q: TCTAGGGCA …ACTTAGCTGTAGTCGTTCTATGGCATATGCTGATCTCGTGCGTCATG… 4

Motivation Large query sizes: Locate genes in large genomes. Find chromosome similarities across different organisms. Chromosomes can be relatively large (e. g. Human Chromosome 1 is approx. 272 million bases). Near homology search: Meaningful for DNA similarity search. Genomes evolve over time due to small mutations. Genomes from different organisms might have high similarity. 5

Problem Statement Given: S: collection of DNA sequences. Q: DNA query sequence. D: similarity measure. Find the most similar subsequence in S with a deviation of at most δ |Q| edit operations. δ at most 15% (near homology search). 6

The Edit Distance [Levenshtein et al. 1966] Measures how dissimilar two strings are. ED (A, B) = minimum number of operations needed to transform A into B. Operations = [insertion, deletion, substitution]. Example: A = ATC and B = ACTG A=A– T C ED (A, B) = 2 B=AC T G 7

The Edit Distance Dynamic Programming Matrix - Match = 0 - In/del/sub = 1 8

The Edit Distance Initialization: 9

The Edit Distance Final Matrix: 10

The Edit Distance Alignment Path: A=A– T C B=AC TG 11

The Edit Distance: Endpoint Subsequence matching Initialization: 12

The Edit Distance: Endpoint Subsequence matching Final Matrix: 13

The Edit Distance: Endpoint Subsequence matching One path: A=AT C B=AC TG 14

Smith-Waterman [Smith&Waterman et al. 1981] Similarity measure used for local alignment: Match can be a subsequence of the query sequence. Define three penalties: match, mismatch, gap. Scoring parameters are defined by the user. Example: A = ATC and B = TATTCG match = 2, mismatch = -1, gap = -1. 15

Smith-Waterman Initialization: 16

Smith-Waterman First column: 17

Smith-Waterman First column: 18

Smith-Waterman Final Matrix: 19

Smith-Waterman Detect highest value: 20

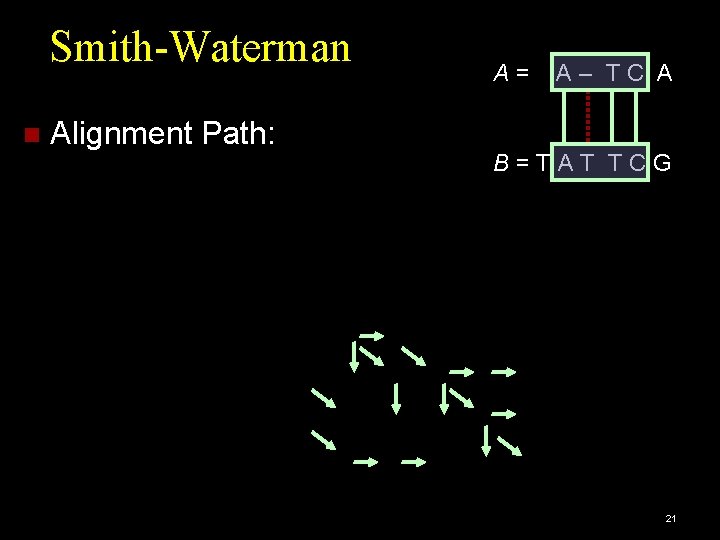
Smith-Waterman Alignment Path: A= A– TC A B=TAT TCG 21

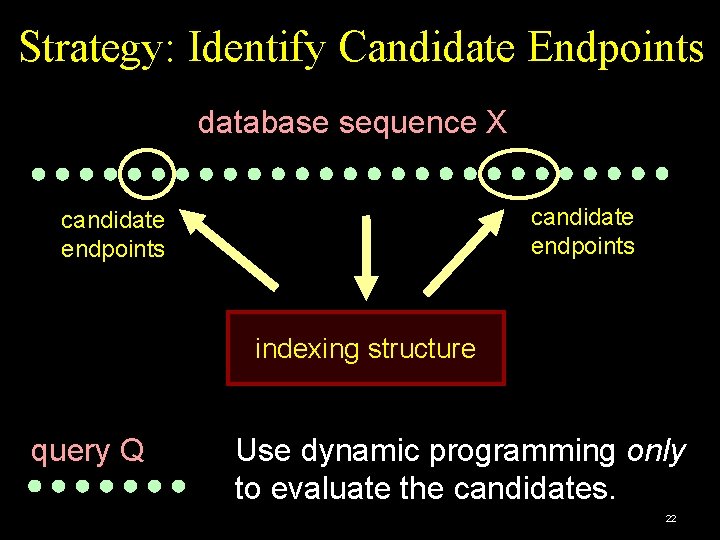
Strategy: Identify Candidate Endpoints database sequence X candidate endpoints indexing structure query Q Use dynamic programming only to evaluate the candidates. 22

RBSA Decompose subsequence matching into two distinct problems: Fixed query length: Assumes all queries have the same length. Variable query length: Uses the solution to the fixed query length problem. Achieves efficient retrieval for queries of arbitrary length. 23

Fixed query length Q: query. (X, t): database position t. Q and (X, t) are mapped into a number: D: the Edit Distance. R: a reference sequence. 24

Lower-bounding the Edit Distance: Metric Property! M (Q, X, t): match of Q in X at position t. X M (Q, X, t) R Q FR (X, t) FR (Q) 25

Database Embedding database X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 sequence 26

Database Embedding database X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 sequence reference set R per DB point 27

Database Embedding database X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 sequence reference set R per DB point query Q 28

Database Embedding database X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 sequence reference set R per DB point query Q query embedding FR (Q) 29

Database Embedding database X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 sequence reference set R per DB point query Q query embedding For each position (X, t): • each Ri is considered. • until an Rj prunes (X, t). FR (Q) Prune using the lower bound 30

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. Xt Q R 1 R 2 R 3 R 4 31

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. ED (Q, X, t) ≥ FRi (X, t) – FRi (Q) Xt Q R 1 R 2 R 3 R 4 32

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. ED (Q, X, t) ≥ FRi (X, t) – FRi (Q) Xt Q R 1 R 2 R 3 R 4 ED (Q, X, t) ≥ 13 -3 = 10 33

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. ED (Q, X, t) ≥ FRi (X, t) – FRi (Q) Xt Q R 1 R 2 R 3 R 4 34

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. ED (Q, X, t) ≥ FRi (X, t) – FRi (Q) Xt Q R 1 R 2 R 3 R 4 ED (Q, X, t) ≥ 14 -3 = 11 35

Filter step Example of filtering: Assume that |Q| = 100 and δ = 10%. We are looking for matches within ED = 10. ED (Q, X, t) ≥ FRi (X, t) – FRi (Q) Xt Q R 1 R 2 R 3 R 4 PRUNE! 36

Refine step Refine only those database positions that were not pruned by filtering. For refinement we can use either the Edit Distance or the Smith-Waterman dynamic programming algorithms. For Smith-Waterman an upper bound can be applied: SW (Q, X, t) ≤ 2|Q| – LBED (Q, X, t) 37

Offline selection of reference sequences Goal: represent each database position (X, t) using a set of reference sequences Rt. Given: Qsample : a set of random queries, of size q. R: a set of random reference sequences of size q. For each (X, t): Choose Rt: that prunes (X, t) for the largest number of queries in Qsample. Greedy selection. 38

Alphabet Reduction Improve filtering power of RBSA by applying alphabet reduction: Σ = {A, C, G, T}. Use four letter collapsing schemes: Scheme 0: no collapsing. Scheme 1: A, C -> X and G, T -> Y. Scheme 2: A, G -> X and C, T -> Y. Scheme 3: A, T -> X and C, G -> Y. The number of possible reference sequences decreases with the alphabet size: 4 q = (2 q)2 vs. 2 q 39

Variable Query Length So far we assumed that |Qi| = q, for every Qi. Q can have arbitrary size: At query time: For simplicity assume that |Q| = αq. Break Q into non-overlapping segments of size q. Two versions of RBSA: Exact and approximate. 40

Exact version Let Xs: t be a subsequence match for Q, within δ |Q|. At least one Qi has within Xs: t a subsequence match within edit distance δ q. α=3 Q 1 q Q Q 2 q Q 3 q …ACTTAGCTGTAGTCGTTCTATGGCATATGCTGATCTCGTGCGTCATG… s Xs: t t 41

Exact version Filter and refine. Break Q into α non-overlapping segments: Q 1, Q 1 q Q Q 2 q Q 2, …, Qα. Q 3 q If for some Qi : ED (Qi, Xs’: t’) ≤ δ q Take the union of all candidates from all Qi s. Perform the refinement step. 42

Approximate version Question: Use only one segment Qi of Q. What is the probability P (Qi) that the subsequence match of Q is included in the candidates of Qi? Proposition: P (Qi) ≥ 50%. Using [Hamza et. al. 1995]. 43

Approximate version By the previous proposition: If a single Qi is chosen and all candidate endpoints are generated, there is at least 50% probability of finding the correct endpoint of the optimal subsequence match. 44

Approximate version By the previous proposition: Assume that the optimal match was not found under Qi. P’ (Qj): probability of not finding the optimal match under Qj, with P’ (Qj) ≤ 0. 5, for j=1, …, α. If we use p segments: Q 1, Q 2, …, Qp P’ (Q 1, Q 2, …, Qp) ≤ (0. 5)p. Thus, the probability of retrieving the optimal match is ≥ 1 – (0. 5)p For p=10, this probability is at least 99. 9%. 45

Experimental Setup Datasets: Database: Human Chromosome 22 (35, 059, 634 bases). Queries: Mouse genome (random chromosomes). Variable size: 40, …, 10 K bases. Similarity to DB varied within 5%, 10% and 15%. Each dataset contains 200 queries. 46

Performance Measures Accuracy: Percentage of queries giving correct results. Efficiency: DP cell cost: cost of dynamic programming, as percentage of brute-force search cost. Retrieval Runtime cost: CPU time per query, as percentage of brute-force CPU time. Brute force: Full Dynamic Programming Algorithm: Edit Distance or Smith-Waterman. 47

Competitors for Endpoint Subsequence Matching: Edit Distance. Q-grams [Burkhardt et al. 1999]. Competitors for Local Alignment: BLAST [Altschul et al. 1990]. BWT-SW [Lam et al. 2008]. 48

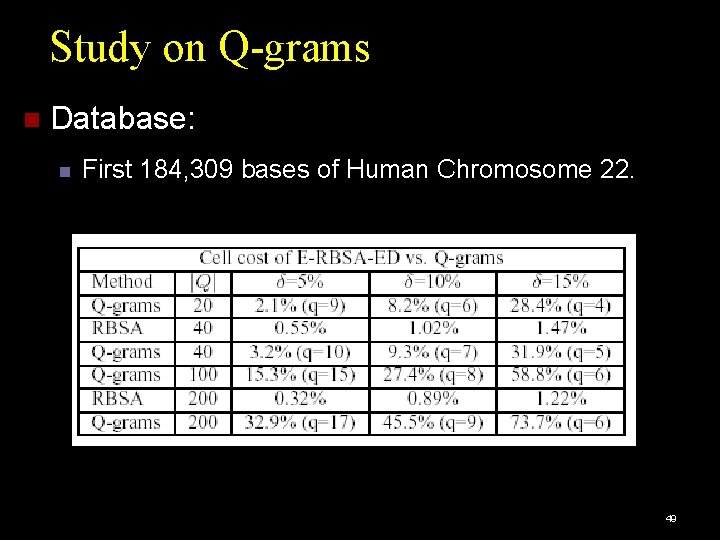
Study on Q-grams Database: First 184, 309 bases of Human Chromosome 22. 49

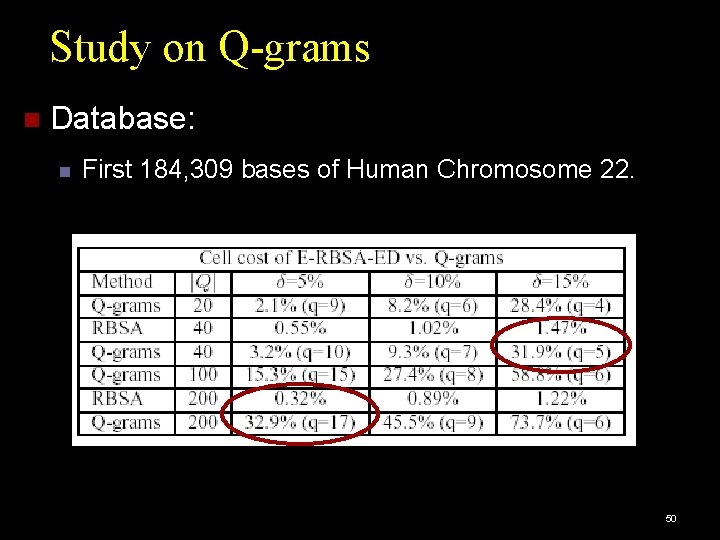
Study on Q-grams Database: First 184, 309 bases of Human Chromosome 22. 50

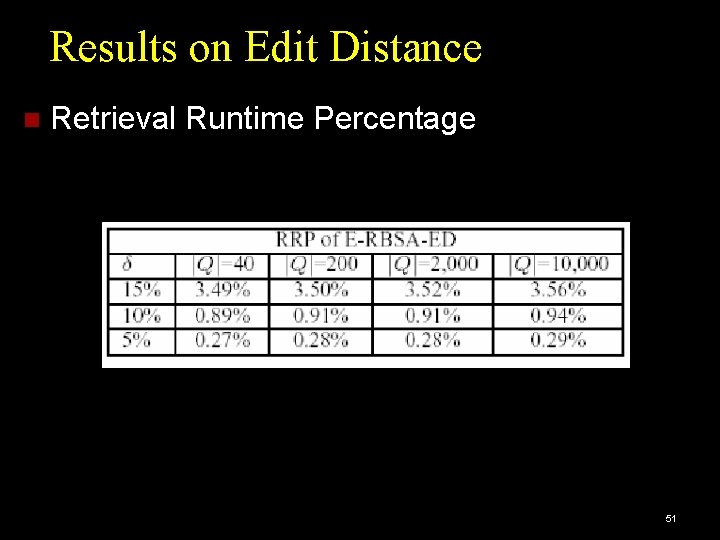
Results on Edit Distance Retrieval Runtime Percentage 51

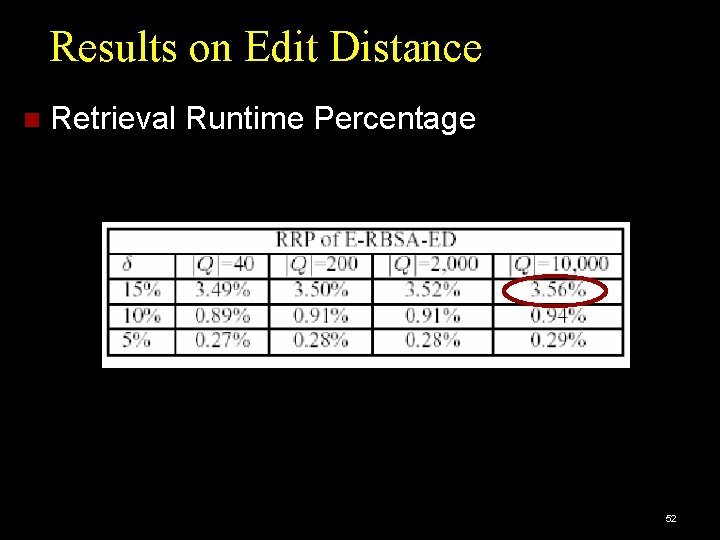
Results on Edit Distance Retrieval Runtime Percentage 52

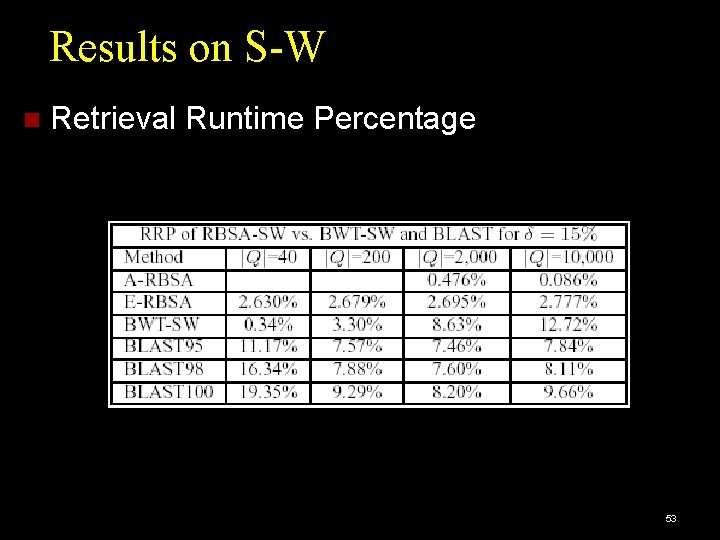
Results on S-W Retrieval Runtime Percentage 53

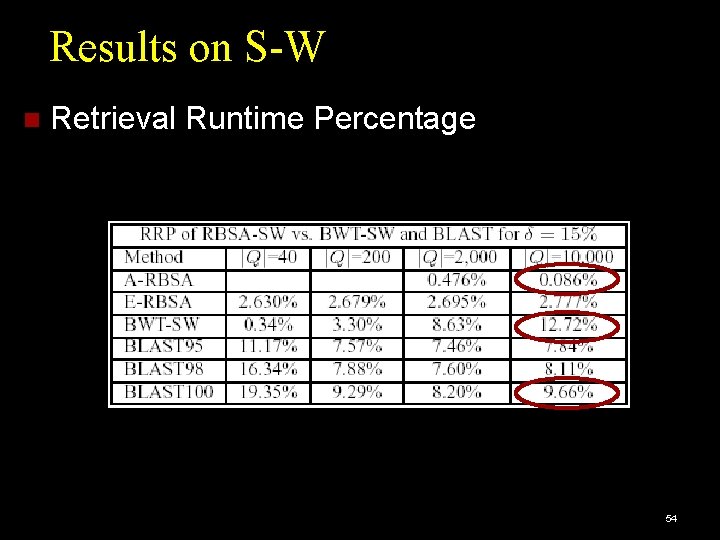
Results on S-W Retrieval Runtime Percentage 54

Conclusions RBSA: identifies subsequence matches in large sequence databases. Two versions: exact and approximate. Is designed for near homology search. Can handle large query sizes. 55

Future Work Perform RBSA on larger genomes and other datasets. Extend RBSA for remote homology search: Proteins: alphabet size is 20. Improve the reference sequence selection process. Reduce the embedding size: Compression techniques. 56

Questions ? 57