Reference Frame Representations The ITRF from the user

Reference Frame Representations: The ITRF from the user perspective Zuheir Altamimi Paul Rebischung Laurent Métivier Xavier Collilieux Kristel Chanard IGN, France Email: zuheir. altamimi@ign. fr Altamimi et al. UAW 2017, Paris

Key Points • Possible reference frame representations and: – the reality of a deformable Earth • Linear motion • Nonlinear variations – technique systematic errors – User needs • The ITRF from the user perspective – Science applications – Operational geodesy – The ITRF should satisfy both types of applications Altamimi et al. UAW 2017, Paris

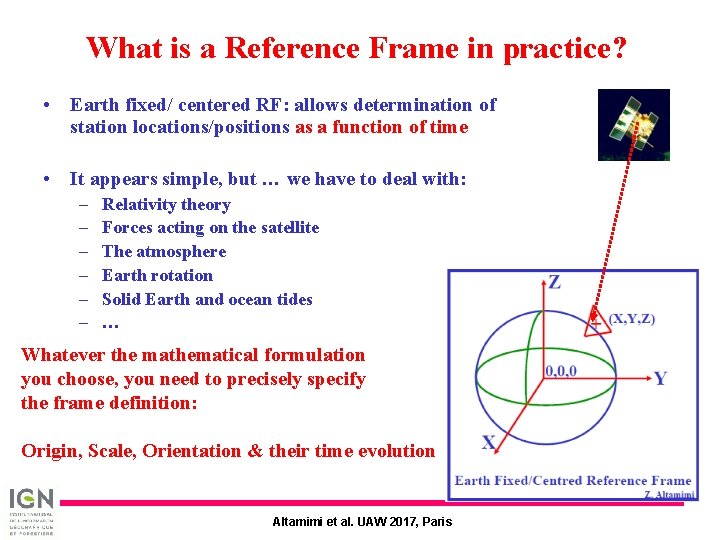
What is a Reference Frame in practice? • Earth fixed/ centered RF: allows determination of station locations/positions as a function of time • It appears simple, but … we have to deal with: – – – Relativity theory Forces acting on the satellite The atmosphere Earth rotation Solid Earth and ocean tides … Whatever the mathematical formulation you choose, you need to precisely specify the frame definition: Origin, Scale, Orientation & their time evolution Altamimi et al. UAW 2017, Paris

Why a Reference System/Frame is needed? • Precise Orbit Determination for: – GNSS: Global Navigation Satellite Systems – Other satellite missions: Altimetry, Oceanography, Gravity • Earth Sciences Applications – – Tectonic motion and crustal deformation Mean sea level variations Earth rotation … • Operational geodesy applications (today: via GNSS only!) – – – National geodetic systems/frames (see next) Positioning : Real Time or a posteriori Navigation: Aviation, Terrestrial, Maritime Require the availability of the orbits and the RF (ITRF) Many, many users… Altamimi et al. UAW 2017, Paris

National/Regional Reference Frames • Use of GNSS technology only (no SLR, VLBI or DORIS) • Use of and rely on the IGS products (orbits, clocks, . . ) • Rely on the ITRF – More than 80% of National RFs are aligned to the ITRF (source: UNGGIM GGRF questionnaire) • Materialized by station coordinates at a given epoch + possibly a deformation model or minimized velocities • May need to apply PSD corrections (if ITRF 2014 is used) • Some countries will move soon to a “dynamic” RF, ITRF-compatible, e. g. Australia Altamimi et al. UAW 2017, Paris

How to define the frame parameters ? • Origin: Co. M (Satellite Techniques, mainly SLR, and potentially DORIS but subject to uncertainties) • Scale: Depends on physical parameters (SLR, VLBI and potentially DORIS, but subject to biases anyway) • Orientation: Conventional • Time evolution: Geophysical meaning (e. g. NNR condition) • ==> Lack of information for some parameters: – Orientation & time evolution (all techniques) – Origin & time evolution in case of VLBI – ==> Rank Deficiency in terms of Normal Equation System Altamimi et al. UAW 2017, Paris

“Motions” of the deformable Earth & technique systematic errors • Nearly linear motion: – Tectonic motion: mainly horizontal (Plate Motion Model) – Post-Glacial Rebound: Vertical & Horizontal • Nonlinear motion: – Loading deformation, including Annual, Semi & Inter-Annual, etc. – Co- & Post-seismic deformations, – Transient deformations, Volcano Eruptions, local events… • Systematic errors, e. g. draconitics, fortnightly, … Altamimi et al. UAW 2017, Paris

Crust-based TRF The instantaneous position of a point on the Earth surface at epoch t could be written as : Altamimi et al. UAW 2017, Paris

Reference Frame Representations • Long-Term linear Frame: mean station positions at a reference epoch (t 0) and station velocities: <= Regularized Position With piece-wise linear function – The indispensable basis for science and operational geodesy applications • Secular Frame + corrections (PSDs, Seasonals, Geocenter motion) ==> modeled “Quasi-Instantaneous” station positions • "Quasi-Instantaneous" RF: mean station positions at a "short” & “regular” interval: – Daily or weekly representations – Nonlinear motion embedded in their time series – Still rely on the ITRF for at least the orientation definition Altamimi et al. UAW 2017, Paris

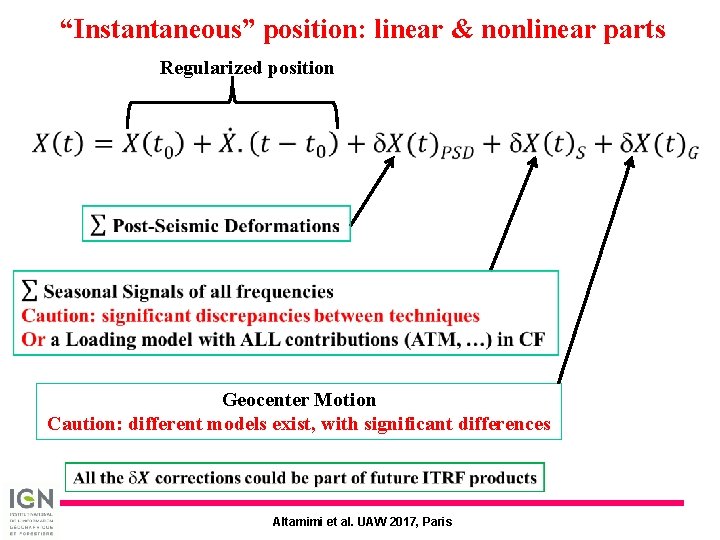
“Instantaneous” position: linear & nonlinear parts Regularized position Geocenter Motion Caution: different models exist, with significant differences Altamimi et al. UAW 2017, Paris

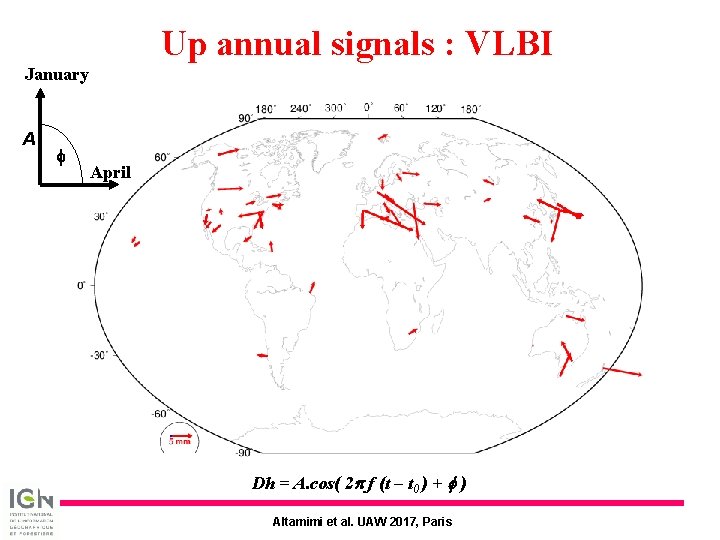
Up annual signals : VLBI January A f April Dh = A. cos( 2 p f (t – t 0 ) + f ) Altamimi et al. UAW 2017, Paris

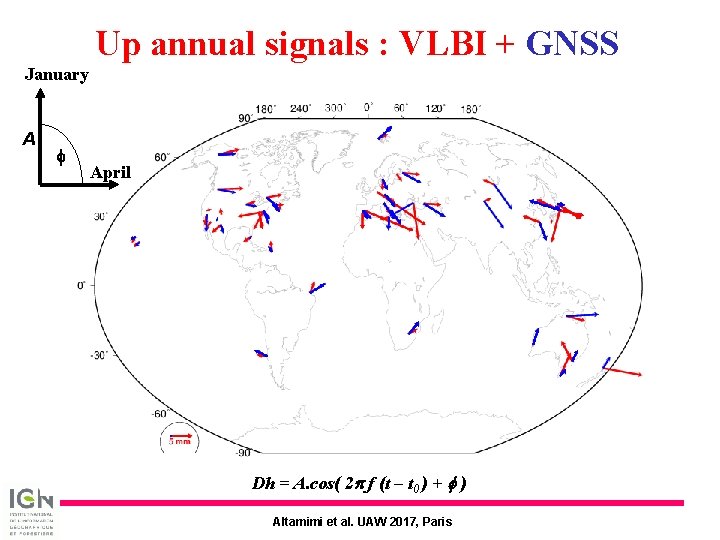
Up annual signals : VLBI + GNSS January A f April Dh = A. cos( 2 p f (t – t 0 ) + f ) Altamimi et al. UAW 2017, Paris

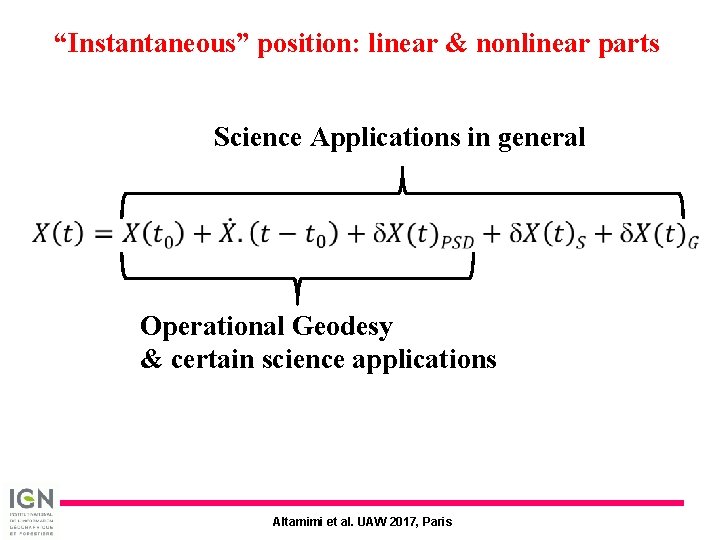
“Instantaneous” position: linear & nonlinear parts Science Applications in general Operational Geodesy & certain science applications Altamimi et al. UAW 2017, Paris

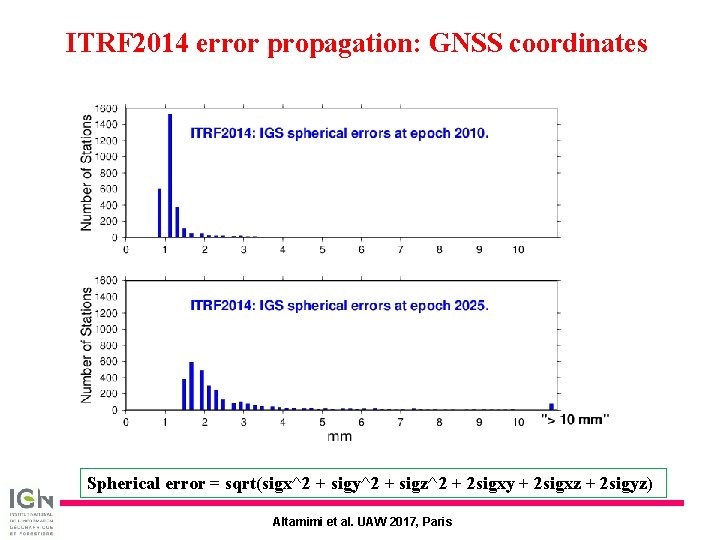
ITRF 2014 error propagation: GNSS coordinates Spherical error = sqrt(sigx^2 + sigy^2 + sigz^2 + 2 sigxy + 2 sigxz + 2 sigyz) Altamimi et al. UAW 2017, Paris

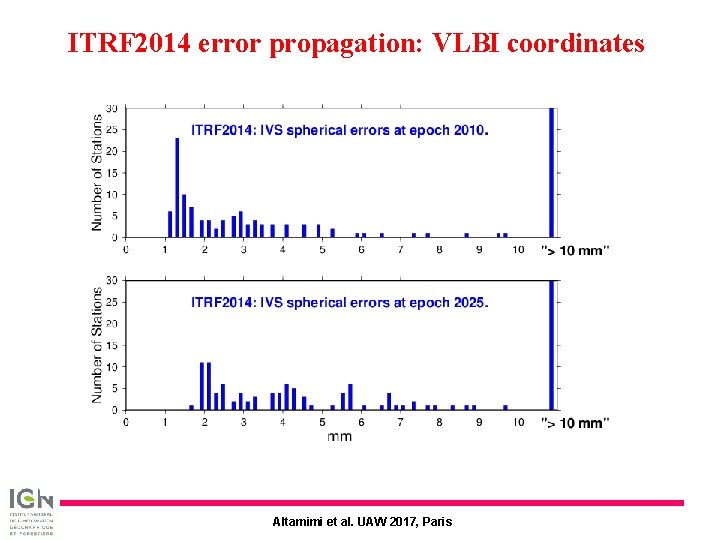
ITRF 2014 error propagation: VLBI coordinates Altamimi et al. UAW 2017, Paris

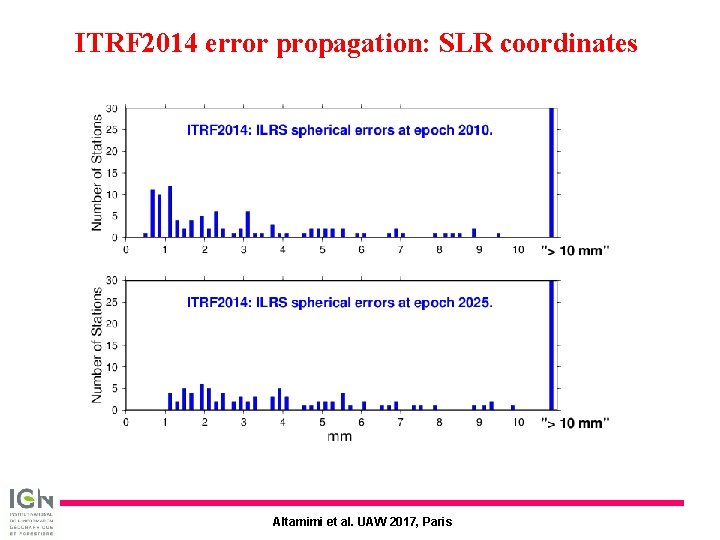
ITRF 2014 error propagation: SLR coordinates Altamimi et al. UAW 2017, Paris

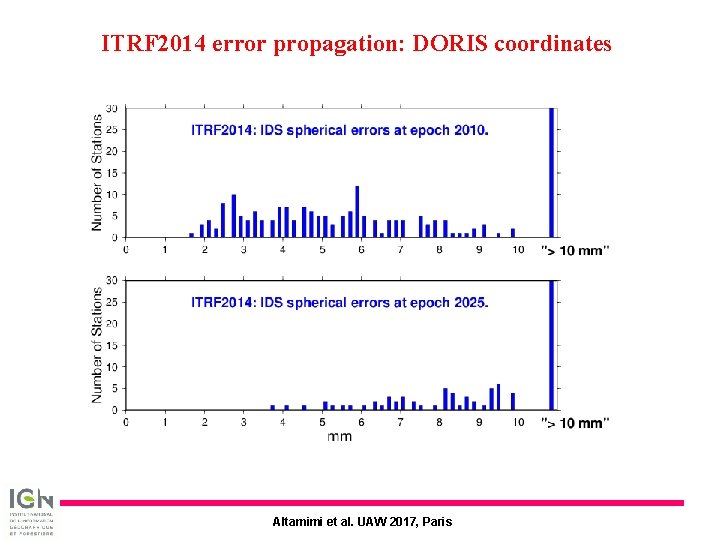
ITRF 2014 error propagation: DORIS coordinates Altamimi et al. UAW 2017, Paris

Conclusion • The ITRF as a secular frame is the basis for Science and operational geodesy applications • ITRF “Instantaneous” station position, if needed, can easily be derived. Cautions: – Seasonal signals: discrepancies among techniques at colocation sites, due to technique systematic errors – Different & discrepant Geocenter motion models exist • Time series of “Quasi-instantaneous” frames: scientifically sound approach. Cautions: – Predictability ? – Less practical for Operational Geodesy & some geophysical applications – Seasonal signals: discrepancies among techniques at colocation sites, due to technique systematic errors – Co-motion constraints at co-location sites ? ? – If needed: Identify users and how to do it ? Altamimi et al. UAW 2017, Paris

Backup Altamimi et al. UAW 2017, Paris

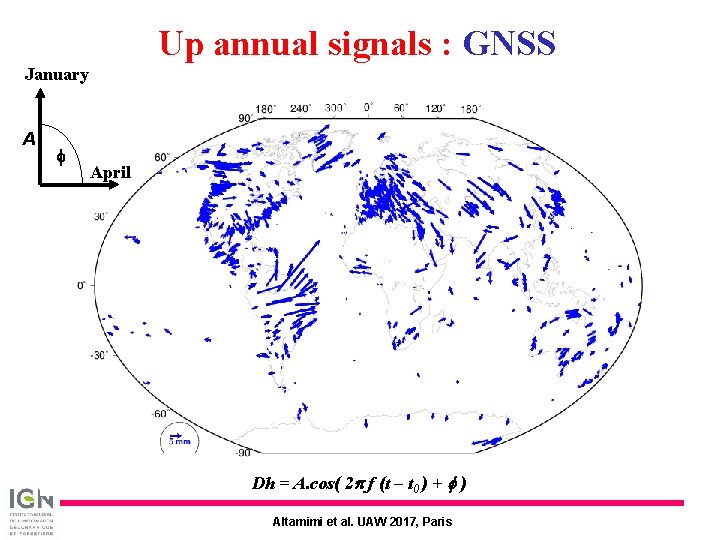
Up annual signals : GNSS January A f April Dh = A. cos( 2 p f (t – t 0 ) + f ) Altamimi et al. UAW 2017, Paris