Reference Angle Reference angle the positive acute angle

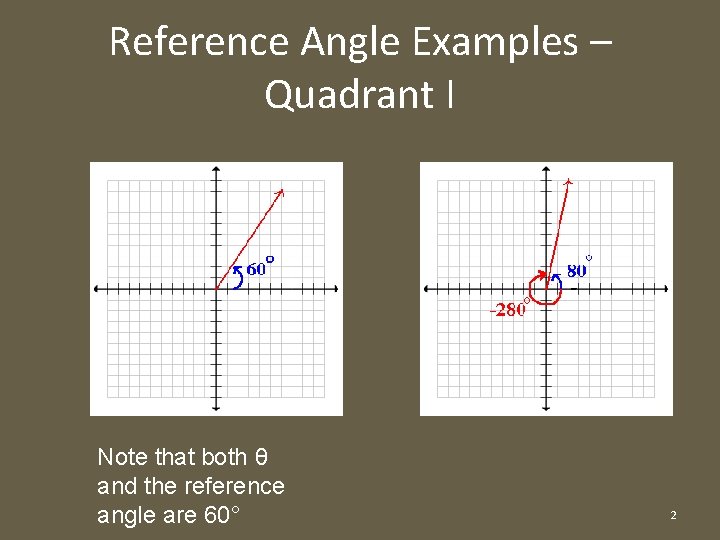
Reference Angle • Reference angle: the positive acute angle that lies between the terminal side of a given angle θ and the x-axis Note: the given angle θ MUST be in standard position 1

Reference Angle Examples – Quadrant I Note that both θ and the reference angle are 60° 2

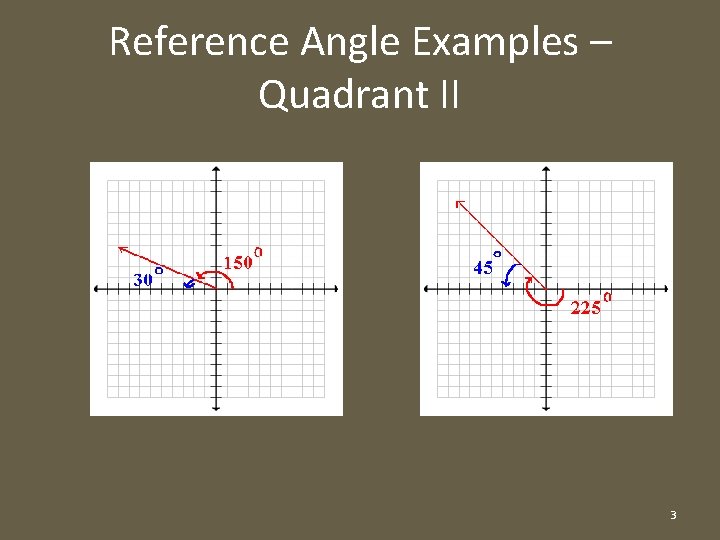
Reference Angle Examples – Quadrant II 3

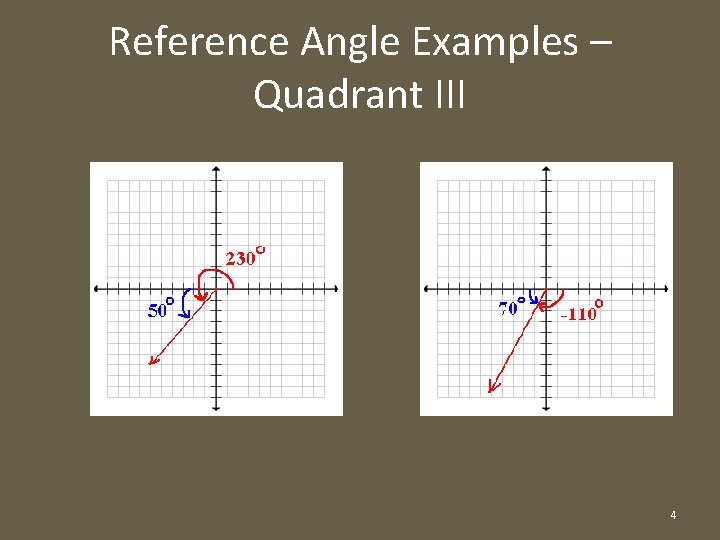
Reference Angle Examples – Quadrant III 4

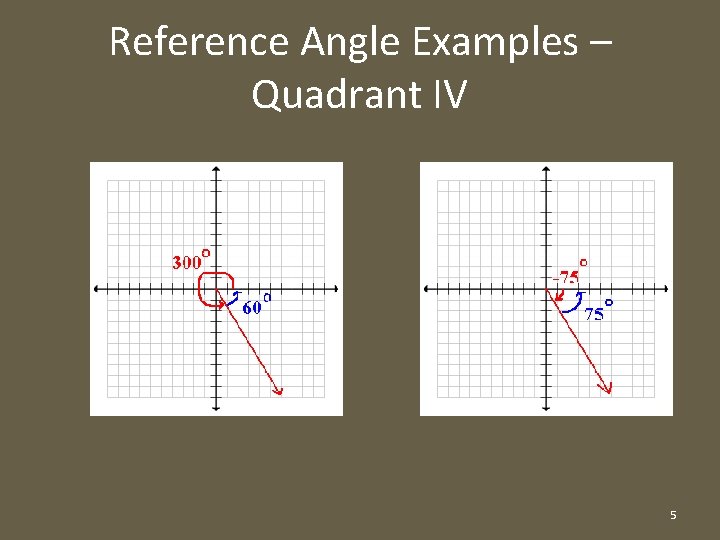
Reference Angle Examples – Quadrant IV 5

Reference Angle Summary • Depending in which quadrant θ terminates, we can formulate a general rule for finding reference angles: – For any positive angle θ, 0° ≤ θ ≤ 360°: • If θ Є QI: Ref angle = θ • If θ Є QII: Ref angle = 180° – θ • If θ Є QIII: Ref angle = θ – 180° • If θ Є QIV: Ref angle = 360° – θ 6

Reference Angle Summary (Continued) – If θ > 360°: • Keep subtracting 360° from θ until 0° ≤ θ ≤ 360° • Go back to the first step on the previous slide – If θ < 0°: • Keep adding 360° to θ until 0° ≤ θ ≤ 360° • Go back to the first step on the previous slide 7

Reference Angle (Example) Ex 1: Draw each angle in standard position and then name the reference angle: a) b) c) d) e) 210° 101° 543° -342° -371° 8

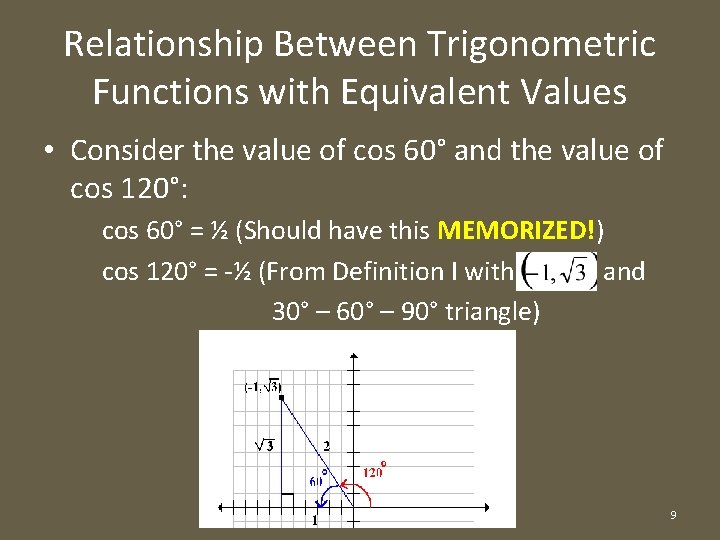
Relationship Between Trigonometric Functions with Equivalent Values • Consider the value of cos 60° and the value of cos 120°: cos 60° = ½ (Should have this MEMORIZED!) cos 120° = -½ (From Definition I with and 30° – 60° – 90° triangle) 9

Relationship Between Trigonometric Functions with Equivalent Values (Continued) • What is the reference angle of 120°? 60° • Need to adjust the final answer depending on which quadrant θ terminates in: 120° terminates in QII AND cos θ is negative in QII • Therefore, cos 120° = -cos 60° = -½ – The VALUES are the same – just the signs are different! 10

Reference Angle Theorem • Reference Angle Theorem: the value of a trigonometric function of an angle θ is EQUIVALENT to the VALUE of the trigonometric function of its reference angle – The ONLY thing that may be different is the sign • Determine the sign based on the trigonometric function and which quadrant θ terminates in – The Reference Angle Theorem is the reason why we need to memorize the exact values of 30°, 45°, and 60° only in Quadrant I! 11

Reference Angle Summary • Recall: – For any positive angle θ, 0° ≤ θ ≤ 360° • If θ Є QI: Ref angle = θ • If θ Є QII: Ref angle = 180° – θ • If θ Є QIII: Ref angle = θ – 180° • If θ Є QIV: Ref angle = 360° – θ 12

Reference Angle Summary (Continued) – If θ > 360°: • Keep subtracting 360° from θ until 0° ≤ θ ≤ 360° • Go back to the first step – If θ < 0°: • Keep adding 360° to θ until 0° ≤ θ ≤ 360° • Go back to the first step 13

Reference Angle Theorem (Example) Ex 2: Use reference angles to find the exact value of the following: a) cos 135° b) tan 315° c) sec(-60°) d) cot 390° 14

Approximating Angles (Continued) • To circumvent this problem, we can use reference angles: – Find the reference angle that corresponds to the given value of a trigonometric function: • Recall that a reference angle is a positive acute angle which terminates in QI • Because cos θ and sin θ are both positive in QI, always use the POSITIVE value of the trigonometric function – Apply the reference angle by utilizing the quadrant in which θ terminates 15

Approximating Angles (Example) Ex 3: Use a calculator to approximate θ if 0° < θ < 360° and: a) b) c) d) cos θ = 0. 0644, θ Є QIV tan θ = 0. 5890, θ Є QI sec θ = -3. 4159, θ Є QII csc θ = -1. 7876, θ Є QIII 16