ReedSolomon Codes RongJaye Chen ReedSolomon Codes 1 Codes

Reed-Solomon Codes Rong-Jaye Chen

Reed-Solomon Codes § § § [1] Codes over GF(2 r) [2] Reed-Solomon codes [3] Decoding Reed-Solomon codes [4] Transform approach to Reed-Solomon codes (Omitted) [5] Berlekamp-Massey algorithm [6] Erasures (Omitted) p 2.

Reed-Solomon Codes § [1] Codes over GF(2 r) § 1. GF(2 r)[x] § § § Polynomials with coefficients from GF(2 r) K[x], K= GF(2)={0, 1}, polynomials with binary coefficients 2. Recall BCH code of length n=2 r-1 § c(x) C iff 1, 2, 3, 4 are all roots of c(x), c(x) K[x] § 1, 2, 4 share same minimal polynomial m 1(x) and 3 has minimal polynomial m 3(x) so the generator polynomial is g. K(x)=m 1(x)m 3(x) p 3.

Reed-Solomon Codes § 3. Generalization of BCH codes § § § Choosing c(x) GF(2 r)[x] c(x) C iff g(x)=(x+ )(x+ 2)(x+ 3)(x+ 4) divides c(x) 4. Subfield subcode § § CK is a BCH code C over GF(2 r) is an example of Reed-Solomon code CK is said to be a subfield subcode of C: § CK C § All words in CK have all their digits in the subfield K of GF(2 r) CK=C Kn Both CK and C are cyclic p 4.

Reed-Solomon Codes § 5. If g(x) generates a linear cyclic code of length 2 r-1 over GF(2 r), the generator of the binary subfield subcode is the polynomial g. K(x) § § Let 1, 2, …, t be distinct non-zero elements of GF(2 r). Then g(x)=( 1+x) ( 2+x)…( t+x) generates a linear cyclic code of length 2 r-1 over GF(2 r) (Theorem 6. 1. 1) Example: § Let F= GF(24) constructed using 1+x+x 4. g(x)=( +x) ( 2+x)= 3+ 5 x+x 2 generates a linear cyclic code over F of length 15. The codeword corresponding to g(x) is of course 3 51000000 p 5.

Reed-Solomon Codes § 6. Cyclic codes over GF(2 r) § Let C be a linear cyclic code of length n over GF(2 r). Every codeword c(x) can be written uniquely as m(x)g(x) for some m(x) in GF(2 r)[x] of degree less than n-deg(g(x)). Also, g(x) divides f(x) iff f(x) is a codeword, and g(x) divides 1+xn (Theorem 6. 1. 3) p 6.

Reed-Solomon Codes § Let g(x) have degree n-k. If g(x) generates a linear cyclic code C over GF(2 r) of length n=2 r-1 then is a generating matrix for C. § |C|=2 rk. There are 2 rk polynomials m(x), since each of the k coefficients in m(x) can be any one of the 2 r field elements p 7.

Reed-Solomon Codes § Example: Construct GF(23) using 1+x+x 3 with as the primitive element. Let g(x)=( +x)( 2+x)= 3+ 4 x+x 2. Then g(x) generates a linear cyclic code C over GF(23) of length n=7 then C has 85 codewords. The codeword corresponding to m(x)=1+ x+ 3 x 4 1 00 3=m, for example, is m(x)g(x) m. G= 30 4 61 3 p 8.

Reed-Solomon Codes § [2] Reed-Solomon codes § 1. Lemma 6. 2. 1 § Let 1, 2, …, t be non-zero elements of GF(2 r). Then p 9.

Reed-Solomon Codes § Example 6. 2. 2 Using lemma 6. 2. 1 and GF(24) constructed using 1+x+x 4, we find that: =( 7+ 2)( 10+ 7) = 12 4 6 = 7 p 10.

Reed-Solomon Codes § 2. Theorem 6. 2. 4 § Let g(x)=( m+1+x)( m+2+x)…( m+ -1+x) be the generator of a linear cyclic code C over GF(2 r) of length n=2 r-1, where is a primitive element in GF(2 r) and m is some integer. Then d(C) <Proof> any -1 rows in the parity check matrix H (see p. 131) is linearly independent so d(C) p 11.

Reed-Solomon Codes § 3. Definition of RS(2 r, ) § § A binary Reed-Solomon code RS(2 r, ) is a cyclic code over GF(2 r) with generator g(x)=( m+1+x)( m+2+x)… ( m+ -1+x) for some integer m and some primitive element of GF(2 r) 4. Theorem 6. 2. 5 § If C is an RS(2 r, ) then (a) n = 2 r-1 (b) k = 2 r- (c) d = (d) |C| = 2 rk p 12.

Reed-Solomon Codes § 5. Binary representation of RS(2 r, ) § § Any RS(2 r, ) code C, can be represented as a binary code simply by replacing each digit in each codeword by the binary word Example: § Let C be the RS(4, 2) with g(x)= +x and where GF(22) is constructed using 1+x+x 2. From Theorem 6. 2. 5, C has n=3, k=2, d=2 and |C|=16, a generating matrix for C is p 13.

Reed-Solomon Codes The 16 messages u with their binary representation along with the corresponding codewords c = u. G of C and their binary representations p 14.

Reed-Solomon Codes § 6. Shortened RS(2 r, ) code C(s) § Example Let C be the RS(4, 2) code of previous example. The shortened RS(4, 2) code C(1) is formed by taking all codewords that have 0’s in the last s=1 position, namely: 000, 10, 2 0 and 1 20 then deleting the last s positions. So C(1)={ 00, 1, 2 , 1 2 } p 15.

Reed-Solomon Codes § The distance d(s) of C(s): d(C(s)) d(C) = d(s) n(s) – k(s) + 1 = 2 r-1 -s-(2 r- -s)+1 = d(s) = § Theorem 6. 2. 12 Let C be an RS(2 r, ) code and let C(s) be the shortened RS(2 r, ) code with parameters n(s), k(s), and d(s), then n(s) = 2 r-1 -s k(s) = 2 r- -s d(s) = p 16.

Reed-Solomon Codes § Example In example 6. 1. 5 we constructed an RS(23, 3) code C with generator polynomial g(x)= 3+ 4 x+x 2. The shortened RS(23, 3) code C(2) has generating matrix and has parameters n(2)=5, k(2)=3 and d(2)=3. G(2) is formed by deleting the last s=2 rows columns of the original matrix G p 17.

Reed-Solomon Codes § [3] Decoding Reed-Solomon codes § 1. Error locations and error magnitudes § § § The error locations of a received word are the coordinates i in which the error pattern is non-zero, referred by an error location number I The error magnitude of an error location i is the element of GF(2 r) that occurs in coordinate i of the error pattern Example 6. 3. 1: Using RS(8, 3) constructed in Example 6. 1. 5, if c= 3 4 00000 is transmitted and w= 3 4 50000 is received then the most likely error pattern is c+w=e=00 40000. So the error location number is 2 and the corresponding error magnitude is 4 p 18.

Reed-Solomon Codes § 2. Decoding algorithm § Notation: g(x)=( m+1+x)( m+2+x)…( m+ -1+x) t= ( -1)/2 a 1, …, ae = the error location numbers b 1, …, be = the error magnitudes p 19.

Reed-Solomon Codes § Symdromes: s = w. H Let w(x)=w 0+w 1 x+ … + wn-1 xn-1 c(x)=c 0+c 1 x+ … + cn-1 xn-1 e(x)=e 0+e 1 x+ … + en-1 xn-1 p 20.

Reed-Solomon Codes § Syndrome: sm+1, …, sm+ -1 sj=w( j) for m+1 j m+ -1 w( j)=c( j)+e( j)= § Error locator polynomial: A(x), let A={a 1, …, ae} A(x)=(a 1 -x) (a 2 -x) … (ae-x) Define j to be the coefficient of xj in A(x)= 0+ 1 x+ … + e-1 xe-1+xe (6. 1) (6. 2) (6. 3) (6. 4) which may be written as (6. 5) p 21.

Reed-Solomon Codes Substitute j=m+1, …, m+e in turn to obtain e linear equations (6. 6) The exe matrix above be called M, which does have full rank p 22.

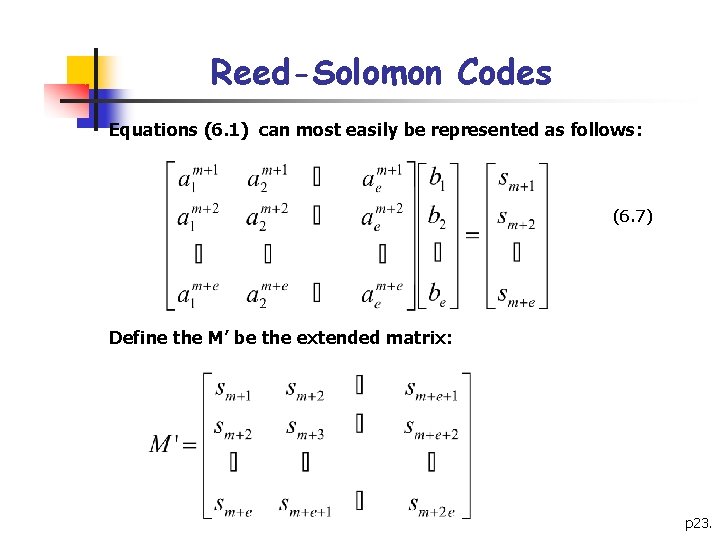
Reed-Solomon Codes Equations (6. 1) can most easily be represented as follows: (6. 7) Define the M’ be the extended matrix: p 23.

Reed-Solomon Codes § Algorithm 6. 3. 2 1. Calculate sj=w( j) for m+1 j m+2 t 2. Setting e=t, find the rank of the extended matrix M’ 3. Let e be the rank of M’ and solve the linear system (6. 6) for 0, …, e-1 4. Find the roots of A(x)= 0+ 1 x+…+ e-1 xe-1+xe § These roots are the error location numbers a 1, …, ae 5. Solve the linear system (6. 7) for b 1, …, be § There are the error magnitudes corresponding to a 1, …, ae p 24.

Reed-Solomon Codes § Example 6. 3. 3 Let g(x)=(1+x)( 2+x)( 3+x)= 6+ 5 x 2+ 2 x 3+x 4 be the generator of an RS(23, 5) code (m=-1, t=2), where GF(23) is constructed using 1+x+x 3. Suppose that the received word is w= 6 5 210 2 Using algorithm 6. 3. 2: 1. Since m=-1 and =5, we calculate the 4 syndromes s 0=w( 0)= 6+ + 5+ 2+1+0+ 2=1 s 1=w( 1)= 6+ 2+ 7+ 5+ 4+0+ 8= 3 s 2=w( 2)= 6+ 3+ 9+ 8+ 8+0+ 14= 3 s 3=w( 3)= 6+ 4+ 11+ 12+0+ 20=1 p 25.

Reed-Solomon Codes 2. Setting e=t=2, the extended matrix M’ is Row reducing M’ yields the matrix which has rank 2 p 26.

Reed-Solomon Codes 3. Since M’ has full rank. e=2 and so we now solve the linear system However, as observed above, we have already row reduced M in Step 2, so we have to solve Then 4 1+ 2=0 so 1= 5, and 0+ 3 5 + 3 = 0 so 0= 1 p 27.

Reed-Solomon Codes 4. We now know the error locator polynomial A(x) = 0+ 1 x+x 2=1+ 5 x+x 2. On substituting field elements into A(x), we find that A( )=0 and A( 6)=0. Therefore A(x)=1+ 5 x+x 2 =( +x)( 6+x) So the error location numbers are a 1= and a 2 = 6 p 28.

Reed-Solomon Codes 5. Now we solve the following linear system: or Then 5 b 2=1 so b 2= 2, and b 1+b 2=1 so b 1= 6. Therefore the most likely error pattern is and the most likely codeword is c = w+e = 6 5 5 2100 p 29.

Reed-Solomon Codes § Example 6. 3. 4 Let be the generator of an RS(24, 7) code (so m=-1 and t=3), where GF(24) is constructed using (see Table 5. 1) Suppose that the received word is p 30.

Reed-Solomon Codes 1. p 31.

Reed-Solomon Codes 2. So M has rank 2 and therefore the most likely error pattern has weight e=2 p 32.

Reed-Solomon Codes 3. With e=2, the linear system (6, 7) becomes but in Step 2 we row reduced this matrix: Then 12 1+ 7=0 so 1= 10, and 7 0+ 1+ 9=0 so 0= 6. p 33.

Reed-Solomon Codes 4. A(x)= 6+ 10 x+x 2=( 2+x)( 4+x). Therefore a 1= 2 and a 2= 4 5. so Therefore b 2= 12 and b 1= 2. So the most likely error pattern is e=00 20 120… 0 and the most likely codeword is c=w+e=1 4 2 12 9100… 0 p 34.

Reed-Solomon Codes § § [4] Transform approach to Reed-Solomon codes (Omitted) [5] Berlekamp-Massey algorithm § 1. Notation § § Reverse error locator polynomial R(x)=1+ t-1 x+ t-2 x 2+…+ 0 xt Syndrome polynomial s(x)=1+sm+1 x+sm+2 x 2+…+sm+2 tx 2 t we can write R(x)s(x)=q(x)x 2 t+1+r(x) with deg(r(x)) t p 35.

Reed-Solomon Codes § § § Produce a sequence of polynomials Pi(x) and integer Di If Pi(x)s(x)=qi(x)xi+1+ri(x) with deg(ri(x)) i , then deg(Pi(x)) i - Di /2 and deg(ri(x)) i - (1+Di)/2 Pi(x) is a combination of Pi-1(x) and some specific previous polynomial Pz(i-1)(x) 2. Algorithm 6. 5. 1 § § Calculate sj=w( j) for m+1 j m+2 t Define: q-1(x)=1+sm+1 x+sm+2 x 2+…+sm+2 tx 2 t q 0(x)=sm+1+sm+2 x+…+sm+2 tx 2 t-1 p-1(x)=x 2 t+1 p 0(x)=x 2 t Let D-1=-1 and D 0=0 and let z 0=-1 p 36.

Reed-Solomon Codes § For 1 i 2 t, recursively define qi(x), pi(x), Di, and zi as follows (a) If qi-1, 0=0, then let qi(x)= qi-1(x)/x pi(x)= pi-1(x)/x Di= 2+Di-1 zi= zi-1 (b) If qi, 0 0, then let p 37.

Reed-Solomon Codes which can be truncated to have degree at most 2 t-1 -i; and let If e t errors have occurred during transmission then p 2 t(x)= R(x) has degree e; the error locator polynomial is: which has e distinct roots p 38.

Reed-Solomon Codes § Example 6. 5. 2: Consider example-6. 3. 4 with the syndrome s 0= 7, s 1= 0, s 2= 9, s 3= 12, s 4= 9, s 5= 7. Working step by step through Algorithm 6. 5. 1, we obtain the following. We begin by setting q-1(x) = 1+ 7 x+x 2+ 9 x 3+ 12 x 4+ 9 x 5+ 7 x 6 q 0(x) = 7+x+ 9 x 2+ 12 x 3+ 9 x 4+ 7 x 5 p-1(x) = x 7 p 0(x) = x 6 D-1 = -1, D 0= 0, z 0= -1 p 39.

Reed-Solomon Codes Let i=1. Since q 0, 0= 7 0, we use step 3(b): (q 0(x)+ 7 q-1(x))/x = 3+x+ 13 x 2+ 14 x 3+ 14 x 4+ 14 x 5 which is truncated to degree 2 t-i-1=4 to give q 1(x) = 3+x+ 13 x 2+ 14 x 3+ 14 x 4 p 1(x) =1+ 7 x D 1 = 2+min{D-1, D 0}=0 and since D 0 D-1, zi=i-1=0 Before proceeding, we shall adopt a more concise format by representing the polynomials by their corresponding words. Then the information we have found so far is the following table: p 40.

Reed-Solomon Codes i -1 0 1 qi - pi Di z i 0 7 0 9 12 9 7 - 0 -1 7 0 9 12 9 7 - 0 0 -1 3 0 13 14 14 0 7 - 1 0 Proceeding from i=2 to i=2 t=6 we obtain the following table i qi pi Di z i -1 0 1 2 3 4 5 6 0 7 0 9 3 0 13 12 7 6 0 10 9 0 0 0 - 0 10 9 12 9 7 - 0 -1 12 9 7 - 0 0 -1 14 14 0 7 - 1 0 12 - 0 8 2 1 0 12 1 - 3 2 0 10 6 4 3 10 6 6 3 6 8 3 So finally we obtain (x) by reading p 2 t(x)= p 6(x)= backwards: (x) = 6 + 10 x+ x 2 p 41.

Reed-Solomon Codes § Example 6. 5. 3: Let C be the RS(24, 9) code with generator g(x)=(1+x)( +x)… ( 7+x) and GF(24) constructed using 1+x+x 4. Suppose that w is the received word and the syndromes of w are: s 0= 12, s 1= 9, s 2= 6, s 3= 3, s 4= 5, s 5= 12, s 6= 6, s 7= 6 Using algorithm 6. 5. 1 and the notation describe in Example 6. 5. 2, we obtain the error locator polynomial as follows: i qi pi Di z i -1 0 1 2 3 4 5 6 7 8 0 12 9 6 3 5 12 6 6 - 0 0 10 7 5 2 - 0 12 1 0 0 0 10 7 5 2 - 0 12 0 8 5 - 0 12 0 0 13 0 - 0 12 13 10 13 Therefore the error locator polynomial is: (x) = 13 + 10 x+ 13 x 2+ 12 x 3+x 4 -1 0 -1 3 5 7 2 4 6 8 0 0 0 4 4 p 42.

Reed-Solomon Codes § 3. Error evaluator polynomial § Since r 2 t(x)=p 2 t(x)q-1(x) mod x 2 t+1 Either r(x)=r 2 t(x) or (x)=r 2 t(x)-p 2 t(x) called the error evaluator polynomial, used to calculate the error magnitudes bj, given the error locations aj § § Example 6. 5. 2 [6] Erasures (Omitted) p 43.