REDUCTION OF COPLANAR FORCES TO A FORCES OR

REDUCTION OF COPLANAR FORCES TO A FORCES OR A COUPLE

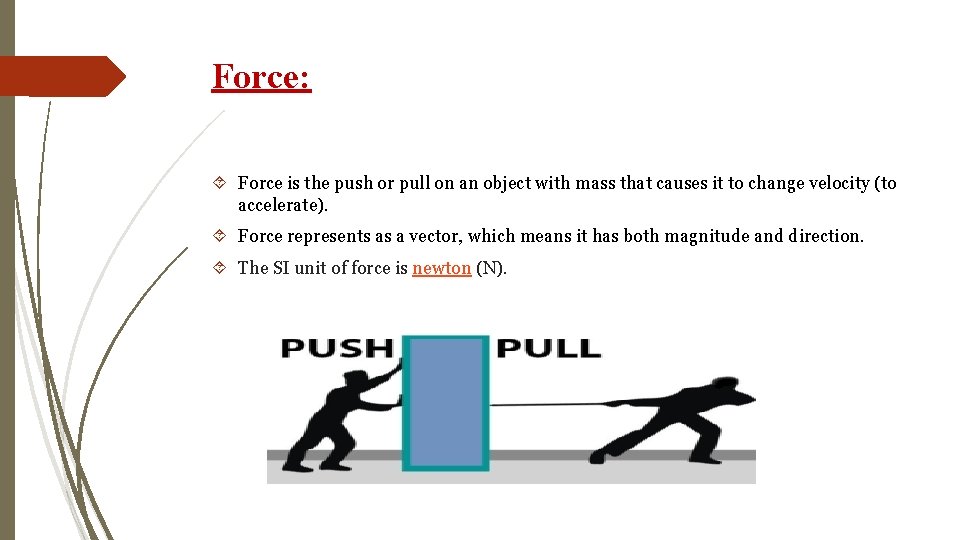
Force: Force is the push or pull on an object with mass that causes it to change velocity (to accelerate). Force represents as a vector, which means it has both magnitude and direction. The SI unit of force is newton (N).

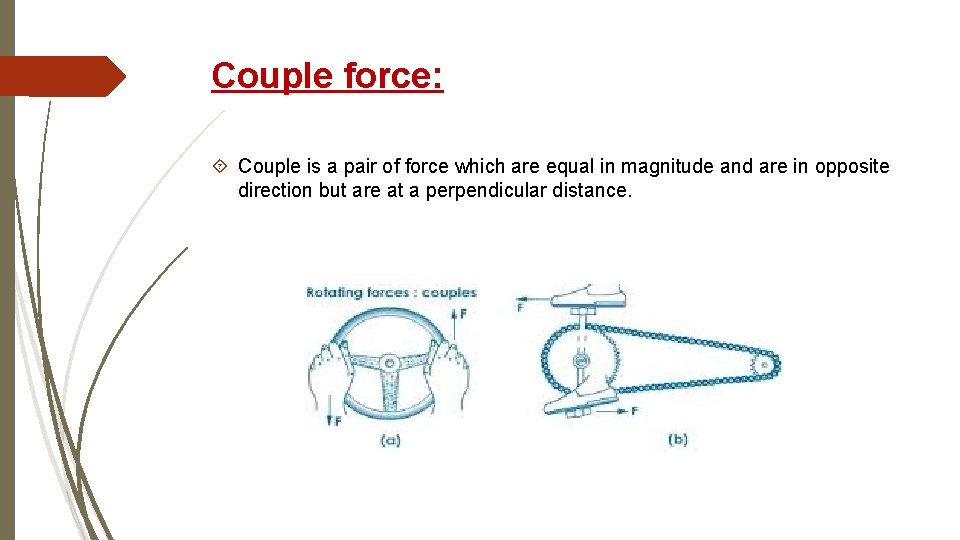
Couple force: Couple is a pair of force which are equal in magnitude and are in opposite direction but are at a perpendicular distance.

Coplanar Forces: Coplanar forces means forces in the plane. When several forces act on a body then they are called force system or system of forces. In the system in which all the forces lies in the same plane then it is known as coplanar force system.

Classification of Coplanar force system: This force system can be concurrent parallel non-concurrent and non-parallel.

Concurrent coplanar force system: The concurrent coplanar force system refers to the number of forces which interest at a common point with their lines of action. It is not recommended that all the separate vectors are to meet at the common point. It is the simplest coplanar force system to resolve to determine the resultant force. Show the concurrent coplanar force system as in Figure:

Parallel coplanar force system: The concurrent coplanar force system refers to the number of forces which are parallel to each other with their lines of action. This force system is mostly used in the analysis of simple beams with number of point loads. Show the parallel coplanar force system as in Figure

Non-parallel and non Concurrent coplanar force system Non-concurrent and non-parallel coplanar force systems refer to the number of forces which are not parallel and do not lie at the common point with their lines of action. It is not the simplest coplanar force system to resolve to determine the resultant force when compared to concurrent and parallel coplanar systems. Show the Non-concurrent and non-parallel coplanar force systems as in Figure

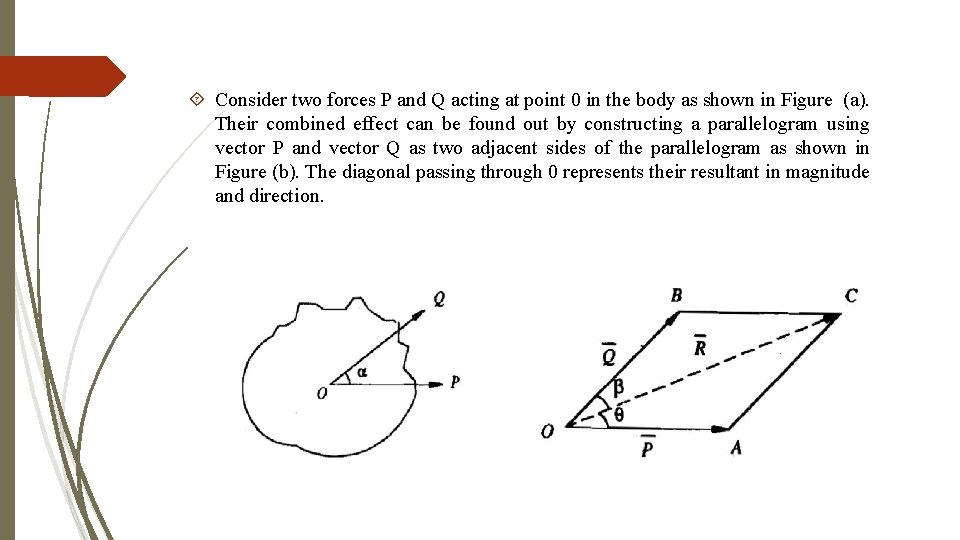
Law of parallelogram of Forces: If the two coplanar forces meet at a point, their resultant may be found by the law of parallelogram of forces, which states that, "If two forces acting at a point are such that they can be represented in magnitude and direction by the two adjacent sides of parallelogram, the diagonal of the parallelogram passing through their point of intersection gives the resultant in magnitude and direction".

Consider two forces P and Q acting at point 0 in the body as shown in Figure (a). Their combined effect can be found out by constructing a parallelogram using vector P and vector Q as two adjacent sides of the parallelogram as shown in Figure (b). The diagonal passing through 0 represents their resultant in magnitude and direction.

You can prove by geometry of the figure that the magnitude R of the resultant and the angle it makes with P are given by where α is the angle between F and 0 θ is the angle between R and P. β is the angle between R and Q. The above two forces can dso be combined by using the law of triangle of forces which ' states that if the second force is drawn from the end of fhe flrst force then the line joining the starting point of fnrst force to the end of the second force represents their resultant.

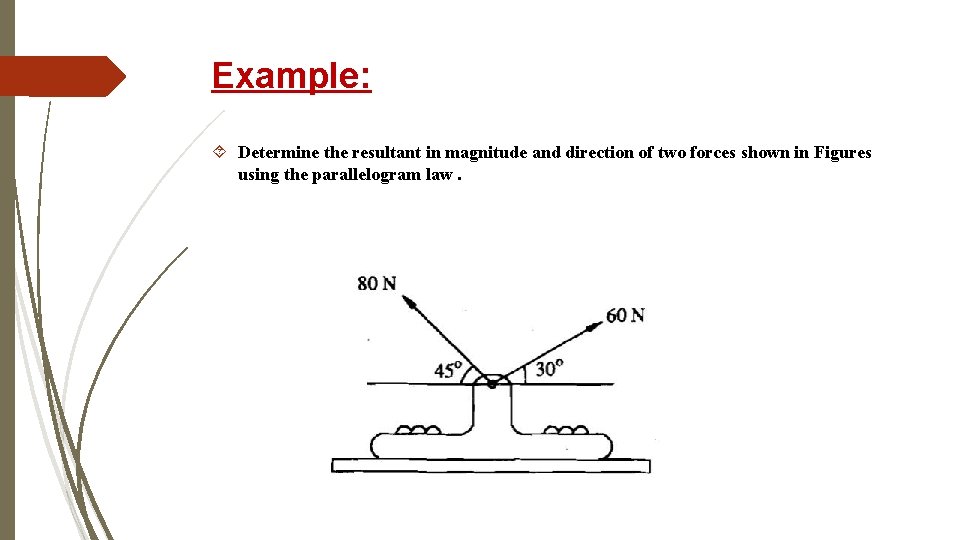
Example: Determine the resultant in magnitude and direction of two forces shown in Figures using the parallelogram law.

Solution: Let P= 60 Nand. Q= 80 N Represent the forces P and Q in magnitude and direction by drawing lines OA and OB to scale and parallel to the lines of action of forces P and Q respectively. Complete the parallelogram of forces. Join OC which is the diagonal of the parallelogram passing through the point of concurrence 'OD of P and Q. the diagonal OC, therefore, represents their resultant in magnitude and direction. Measure the length OC and get the magnitude of the resultant. Measure angle COA and get the direction of the resultant with respect to force P.

Using trigonometrical relations, we get,

Resultant of coplanar concurrent forces: The resultant of a concurrent force system can be defined as the simplest single force which can replace the original system without changing its external effect on a rigid body. The technique of resolution of a force can be used to determine the resultant of coplanar concurrent forces. If 'n' concurrent forces F! , F 2 , F 3 , . . . , F, are acting at a point in a body then each force can be resolved into two mutually perpendicular directions. Thus, we get '2 n' components. Each set of 2 n components acts in one direction only. Therefore, we can algebraically add all these components to get the components of the resultant.

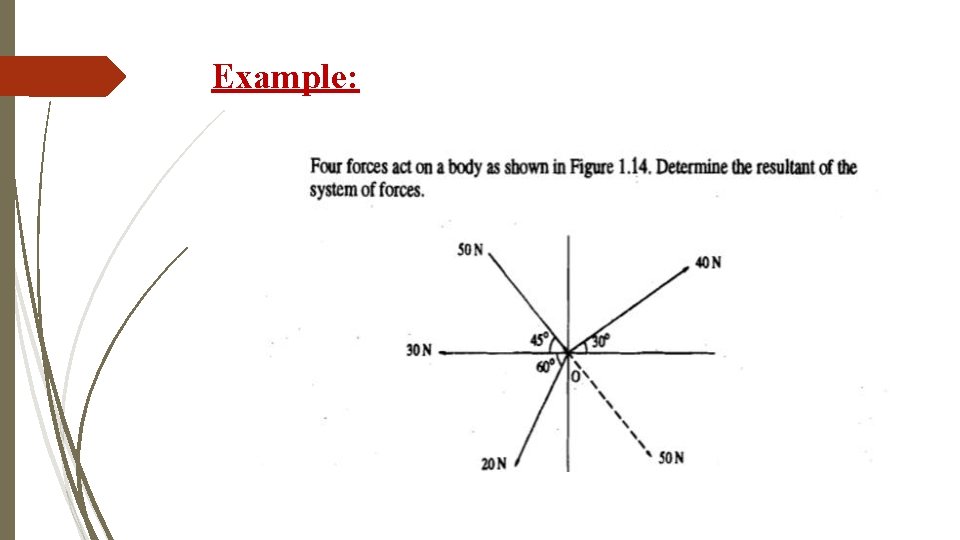
Example:

Solution: Note : The angle made by 50 N force is measured in anticlockwise direction from positive x axis after making the force act away from 0 by principle of transmissibility of the force. R, = 40 cos 30’+50 cos 45 -30 cos 0 -20 cos 60 0 <(less than equal) 90' may be chosen in appropriate quadrant with proper signs as indicated above

SUMMARY: Force Push or pull Coplanar Forces acting in one plane Concurrent Forces Lines of action of forces pass through a common point Parallel Forces Lines of action of forces are parallel to each other. Resolution of a Force Splitting a force into its components. Generally the force are resolved along two mutually perpendicular axes e. g. x and y axes. Resultant A single force which has the same effect on the body as all the forces acting together are having. A resultant is equivalent to the system of force. A couple consists of two forces equal in magnitude, parallel but oppositely directed. Couple