Reduced Mass system 1 For a circular orbit

Reduced Mass system 1. For a circular orbit, compute the orbital velocity of a lower mass object, m 2, about a higher mass object, m 1: (a) assuming that m 1 >> m 2, so that you can treat m 1 to be stationary. This is the type of computation you would do in introductory physics. (b) using the transformation to the 1 -body problem. Is your answer smaller or larger than in part (a), and if so by what fraction? (c) transforming back from the 1 -body problem to the 2 -body problem, what is the velocity of m 1 and m 2 about the center of mass?

Reduced Mass system 1. For a circular orbit, compute the orbital velocity of a lower mass object, m 2, about a higher mass object, m 1: a) assuming that m 1 >> m 2, so that you can treat m 1 to be stationary. This is the type of computation you would do in introductory physics.

Reduced Mass system 1. For a circular orbit, compute the orbital velocity of a lower mass object, m 2, about a higher mass object, m 1: (b) using the transformation to the 1 -body problem. Is your answer smaller or larger than in part (a), and if so by what fraction?

Reduced Mass system 1. For a circular orbit, compute the orbital velocity of a lower mass object, m 2, about a higher mass object, m 1: (b) using the transformation to the 1 -body problem. Is your answer smaller or larger than in part (a), and if so by what fraction? compare with where M = m 1 + m 2. Answer is larger by:

Reduced Mass system 1. For a circular orbit, compute the orbital velocity of a lower mass object, m 2, about a higher mass object, m 1: (c) transforming back from the 1 -body problem to the 2 -body problem, what is the velocity of m 1 and m 2 about the center of mass?

Reduced Mass system 2. Show that the total energy and orbital angular momentum of two bodies with masses m 1 and m 2 orbiting each other about their center of mass is equal to the total energy and orbital angular momentum of a reduced mass μ = m 1 m 2/(m 1 + m 2) orbiting a mass M = m 1 + m 2 having the same orbital eccentricity and orbital separation as that of m 1 and m 2 (see lecture notes).

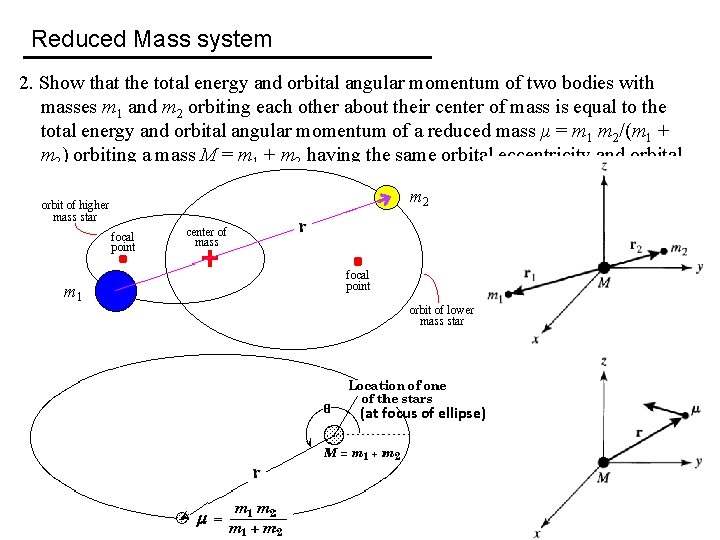
Reduced Mass system 2. Show that the total energy and orbital angular momentum of two bodies with masses m 1 and m 2 orbiting each other about their center of mass is equal to the total energy and orbital angular momentum of a reduced mass μ = m 1 m 2/(m 1 + m 2) orbiting a mass M = m 1 + m 2 having the same orbital eccentricity and orbital separation as that of m 1 and m 2 (see lecture notes). m 2 m 1 (at focus of ellipse)

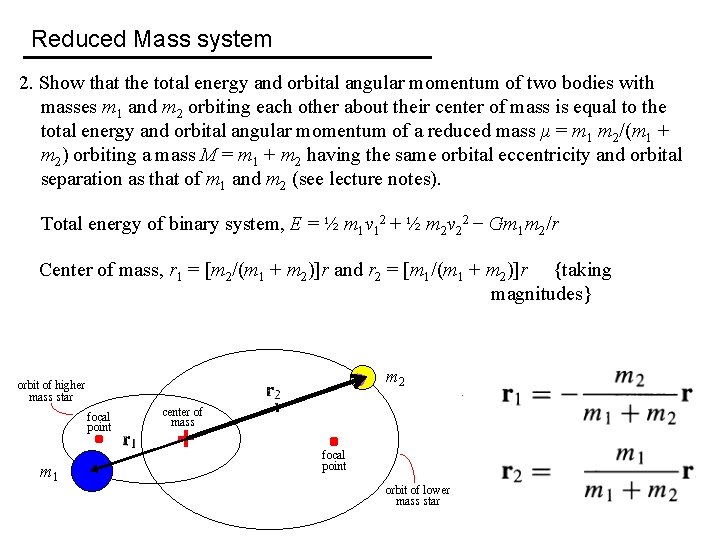
Reduced Mass system 2. Show that the total energy and orbital angular momentum of two bodies with masses m 1 and m 2 orbiting each other about their center of mass is equal to the total energy and orbital angular momentum of a reduced mass μ = m 1 m 2/(m 1 + m 2) orbiting a mass M = m 1 + m 2 having the same orbital eccentricity and orbital separation as that of m 1 and m 2 (see lecture notes). Total energy of binary system, E = ½ m 1 v 12 + ½ m 2 v 22 − Gm 1 m 2/r Center of mass, r 1 = [m 2/(m 1 + m 2)]r and r 2 = [m 1/(m 1 + m 2)]r {taking magnitudes} m 2 m 1

Reduced Mass system 2. Show that the total energy and orbital angular momentum of two bodies with masses m 1 and m 2 orbiting each other about their center of mass is equal to the total energy and orbital angular momentum of a reduced mass μ = m 1 m 2/(m 1 + m 2) orbiting a mass M = m 1 + m 2 having the same orbital eccentricity and orbital separation as that of m 1 and m 2 (see lecture notes). Total energy of binary system, E = ½ m 1 v 12 + ½ m 2 v 22 − Gm 1 m 2/r Thus, E = ½ m 1 v 12 + ½ m 2 v 22 − Gm 1 m 2/r = ½ m 1(μ/m 1)2 v 2 + ½ m 2(μ/m 2)2 v 2 − Gm 1 m 2/r = ½ μv 2 − GMμ/r

Reduced Mass system 2. Show that the total energy and orbital angular momentum of two bodies with masses m 1 and m 2 orbiting each other about their center of mass is equal to the total energy and orbital angular momentum of a reduced mass μ = m 1 m 2/(m 1 + m 2) orbiting a mass M = m 1 + m 2 having the same orbital eccentricity and orbital separation as that of m 1 and m 2 (see lecture notes). Orbital angular momentum of binary system, L = m 1 r 1 × v 1 + m 2 r 2 × v 2 Thus, L = m 1 r 1 × v 1 + m 2 r 2 × v 2 (μ/m 2)v = m 1 r 1 × [−(μ/m 1)v] + m 2 r 2 × = −μr 1 × v + μr 2 × v = μ(r 2 −r 1) × v = μr × v

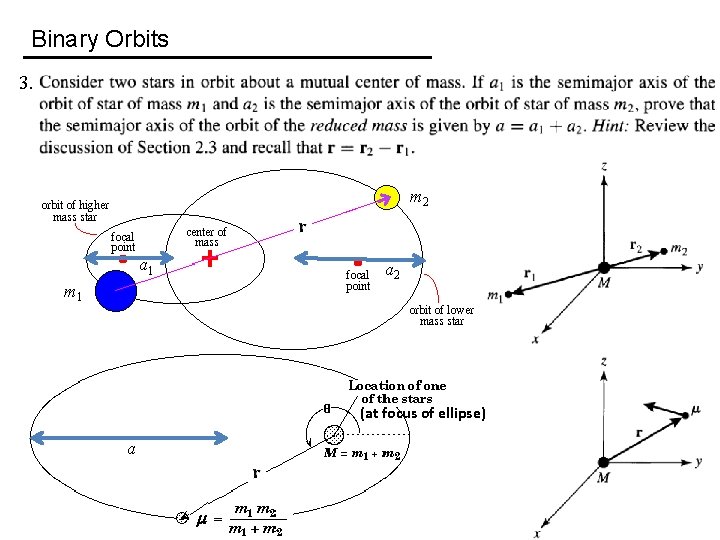
Binary Orbits 3. m 2 a 1 a 2 m 1 (at focus of ellipse) a

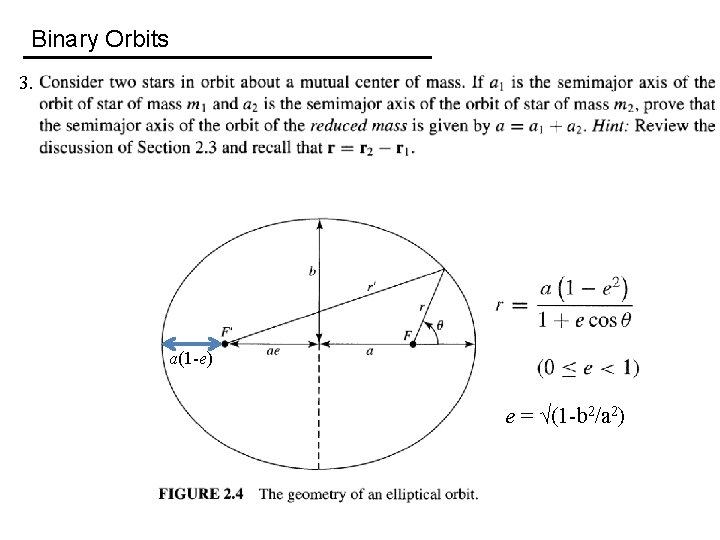
Binary Orbits 3. a(1 -e) e = √(1 -b 2/a 2)

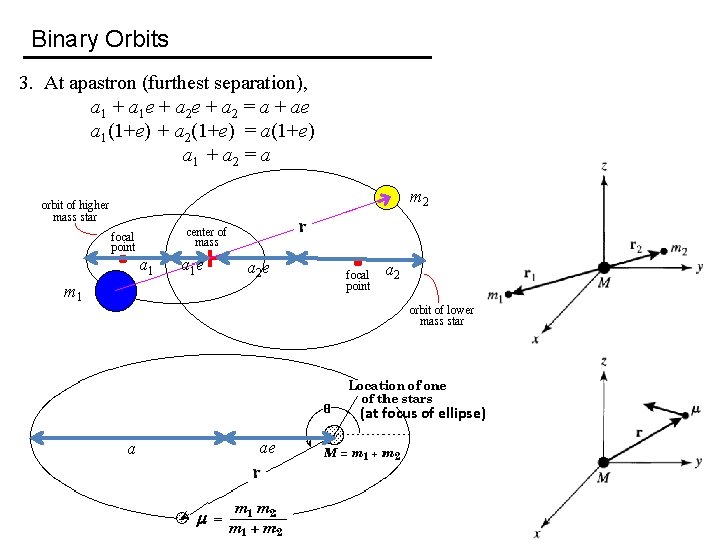
Binary Orbits 3. At apastron (furthest separation), a 1 + a 1 e + a 2 = a + ae a 1(1+e) + a 2(1+e) = a(1+e) a 1 + a 2 = a m 2 a 1 e a 2 e m 1 a 2 (at focus of ellipse) ae a

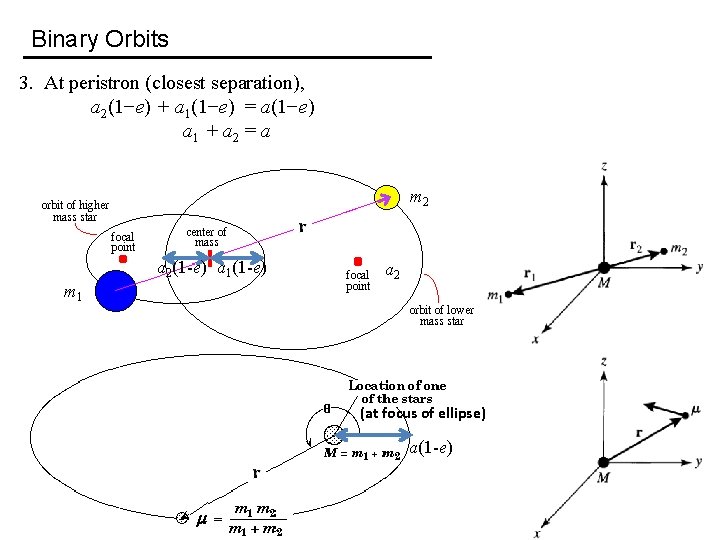
Binary Orbits 3. At peristron (closest separation), a 2(1−e) + a 1(1−e) = a(1−e) a 1 + a 2 = a m 2 a 2(1 -e) a 1(1 -e) m 1 a 2 (at focus of ellipse) a(1 -e)

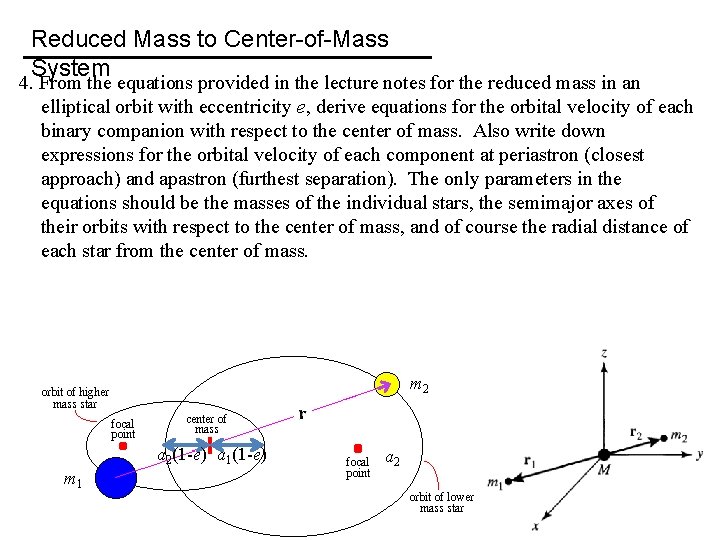
Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest approach) and apastron (furthest separation). The only parameters in the equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. m 2 a 2(1 -e) a 1(1 -e) m 1 a 2

Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest approach) and apastron (furthest separation). The only parameters in the equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. At periastron, r 1 = a 1 (1 – e) and r 2 = a 2 (1 – e). From center of mass, r = r 1(m 1 + m 2)/m 2 and r = r 2(m 1 + m 2)/m 1

Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest approach) and apastron (furthest separation). The only parameters in the equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. Orbital velocity of reduced mass v 2 = G(m 1 + m 2)(2/r – 1/a) Now, v 1 = (μ/m 1)v = [m 2/(m 1 + m 2)] v Thus, v 12 = [m 2/(m 1 + m 2)]2 v 2 = [m 2/(m 1 + m 2)]2 Gm 2(2/r 1 – 1/a 1)

Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest approach) and apastron (furthest separation). The only parameters in the equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. Orbital velocity of reduced mass v 2 = G(m 1 + m 2)(2/r – 1/a) Now, v 2 = (μ/m 2)v = [m 1/(m 1 + m 2)] v Thus, v 22 = [m 1/(m 1 + m 2)]2 v 2 = [m 1/(m 1 + m 2)]2 Gm 1(2/r 2 – 1/a 2)

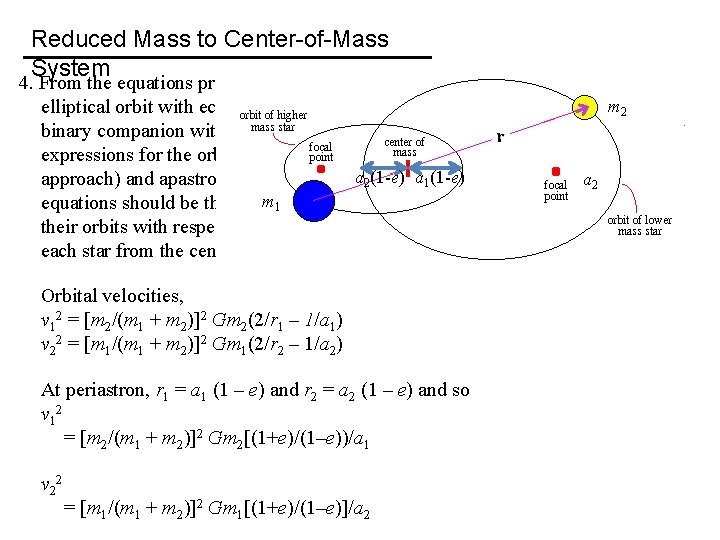
Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an m 2 elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest a 2(1 -e) a 1(1 -e) a 2 approach) and apastron (furthest separation). The only parameters in the m 1 equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. Orbital velocities, v 12 = [m 2/(m 1 + m 2)]2 Gm 2(2/r 1 – 1/a 1) v 22 = [m 1/(m 1 + m 2)]2 Gm 1(2/r 2 – 1/a 2) At periastron, r 1 = a 1 (1 – e) and r 2 = a 2 (1 – e) and so v 1 2 = [m 2/(m 1 + m 2)]2 Gm 2[(1+e)/(1–e))/a 1 v 2 2 = [m 1/(m 1 + m 2)]2 Gm 1[(1+e)/(1–e)]/a 2

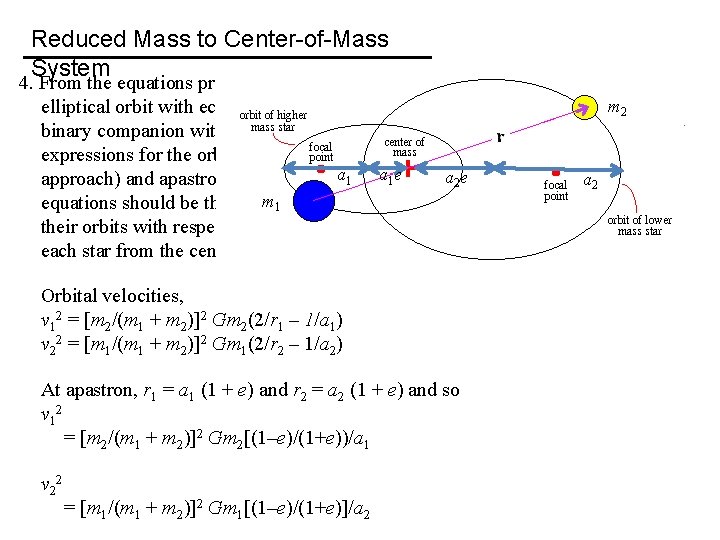
Reduced Mass to Center-of-Mass System 4. From the equations provided in the lecture notes for the reduced mass in an m 2 elliptical orbit with eccentricity e, derive equations for the orbital velocity of each binary companion with respect to the center of mass. Also write down expressions for the orbital velocity of each component at periastron (closest a 1 e a 2 approach) and apastron (furthest separation). The only parameters in the m 1 equations should be the masses of the individual stars, the semimajor axes of their orbits with respect to the center of mass, and of course the radial distance of each star from the center of mass. Orbital velocities, v 12 = [m 2/(m 1 + m 2)]2 Gm 2(2/r 1 – 1/a 1) v 22 = [m 1/(m 1 + m 2)]2 Gm 1(2/r 2 – 1/a 2) At apastron, r 1 = a 1 (1 + e) and r 2 = a 2 (1 + e) and so v 1 2 = [m 2/(m 1 + m 2)]2 Gm 2[(1–e)/(1+e))/a 1 v 2 2 = [m 1/(m 1 + m 2)]2 Gm 1[(1–e)/(1+e)]/a 2

Eclipsing Spectroscopic Binaries 5. r 2 r 1 a

Eclipsing Spectroscopic Binaries 5. Inclination of orbit, cos(i) > (r 1 + r 2) / a r 2 i r 1 a r 1

Eclipsing Spectroscopic Binaries 5. Inclination of orbit, cos(i) > (r 1 + r 2) / a > (10 + 1) / 430. 2 > 88 o. 5 r 2 i r 1 a r 1

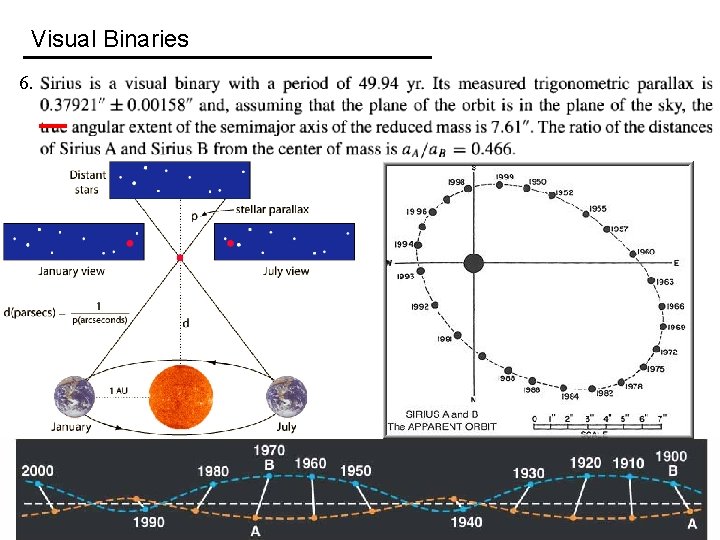
Visual Binaries 6.

Visual Binaries 6. Distance of Sirius, d = 1/p , ∂d = −∂p /(p )2 = 2. 64 ± 0. 01 pc Mass ratio, m. B/m. A = a. A/a. B = 0. 466 Total mass, m. A + m. B = 4π2 a 3/GP 2 Thus, m. A + 0. 466 m. A = (3. 258 ± 0. 025) M m. A = (2. 222 ± 0. 017) M

Visual Binaries 6. Distance of Sirius, d = 1/p , ∂d = −∂p /(p )2 = 2. 64 ± 0. 01 pc Mass ratio, m. B/m. A = a. A/a. B = 0. 466 Total mass, m. A + m. B = 4π2 a 3/GP 2 Thus, m. B/0. 466 + m. B = (3. 258 ± 0. 025) M m. B = (1. 036 ± 0. 008) M

Visual Binaries 6. Luminosity, L*/L = 100(M − M*)/5 , where L is the luminosity of the Sun. Absolute bolometric magnitude of the Sun, M = +4. 74 Luminosity of Sirius A, LA = 22. 5 L Luminosity of Sirius B, LB = 0. 02 L

Visual Binaries 6. Luminosity of blackbody, L = 4πR 2 σT 4 so that RB = = (5. 34 ± 0. 04) × 106 m = (0. 00797 ± 0. 0006) R = (0. 837 ± 0. 006) RE

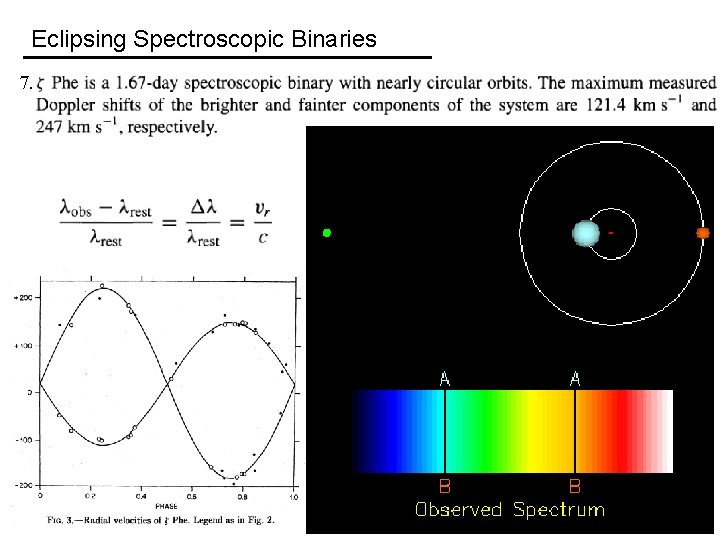
Eclipsing Spectroscopic Binaries 7.

Eclipsing Spectroscopic Binaries 7. Denoting the mass of brighter star as m 1 and mass of dimmer star as m 2, mass ratio m 1/m 2 = v 2 r /v 1 r = 247/121. 4 = 2. 03 Total mass, (m 1 + m 2) sin 3 i = = 1. 72 × 1031 kg = 8. 7 M Thus, (m 1 + m 1/2. 03) sin 3 i = 1. 72 × 1031 kg m 1 sin 3 i = 1. 15 × 1031 kg = 5. 8 M

Eclipsing Spectroscopic Binaries 7. Denoting the mass of brighter star as m 1 and mass of dimmer star as m 2, mass ratio m 1/m 2 = v 2 r /v 1 r = 247/121. 4 = 2. 03 Thus, (2. 03 m 2 + m 2) sin 3 i = 1. 72 × 1031 kg m 2 sin 3 i = 5. 68 × 1030 kg = 2. 9 M

Eclipsing Spectroscopic Binaries 7. For <sin 3 i> ≅ 2/3, kg m 1 = 1. 72 × 1031 = 8. 7 M kg m 2 = 8. 52 × 1030 = 4. 3 M

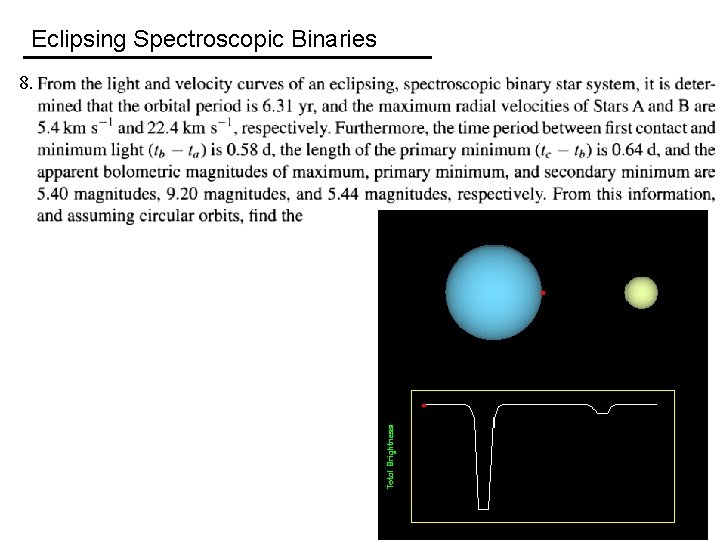
Eclipsing Spectroscopic Binaries 8.

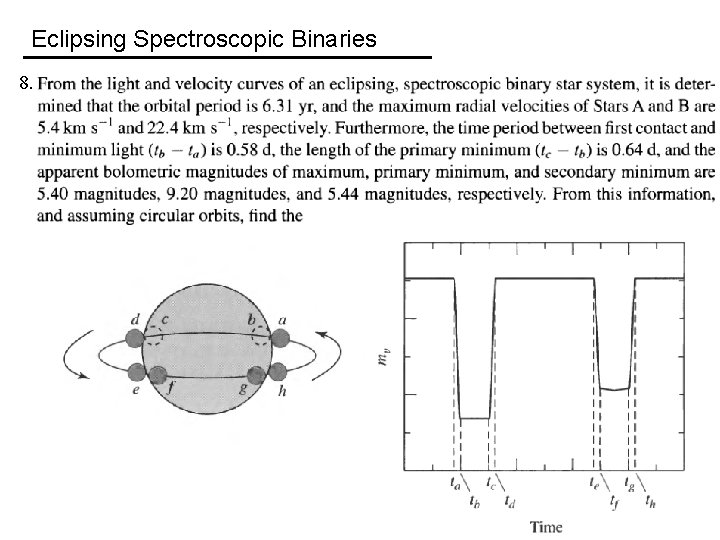
Eclipsing Spectroscopic Binaries 8.

Eclipsing Spectroscopic Binaries 8.

Eclipsing Spectroscopic Binaries 8. m. A / m. B = v. Br / v. Ar = 22. 4 / 5. 4 = 4. 148

Eclipsing Spectroscopic Binaries 8.

Eclipsing Spectroscopic Binaries 8. m. A + m. B = = 1. 02 × 1031 kg = 5. 1 M

Eclipsing Spectroscopic Binaries 8. m. A + m. A/4. 148 = 1. 02 × 1031 kg m. A = 8. 32 × 1030 kg = 4. 2 M (Notice that v. Ar < v. Br) 4. 148 m. B + m. B = 1. 02 × 1031 kg m. B = 1. 98 × 1030 kg = 1. 0 M (Notice that v. Br > v. Ar)

Eclipsing Spectroscopic Binaries 8. m = 5. 40 m = 5. 44 m = 9. 20

Eclipsing Spectroscopic Binaries 8. Note: not enough information to determine which star is larger. I assume here that the more massive star is larger. r. B = r. A =B = 6. 97 × 108 m = 1. 0 R = 1. 44 × 109 m = 2. 1 R

Eclipsing Spectroscopic Binaries 8. (TA / TB)4 = 26. 8 TA / TB = 2. 3 m = 5. 40 m = 5. 44 m = 9. 20

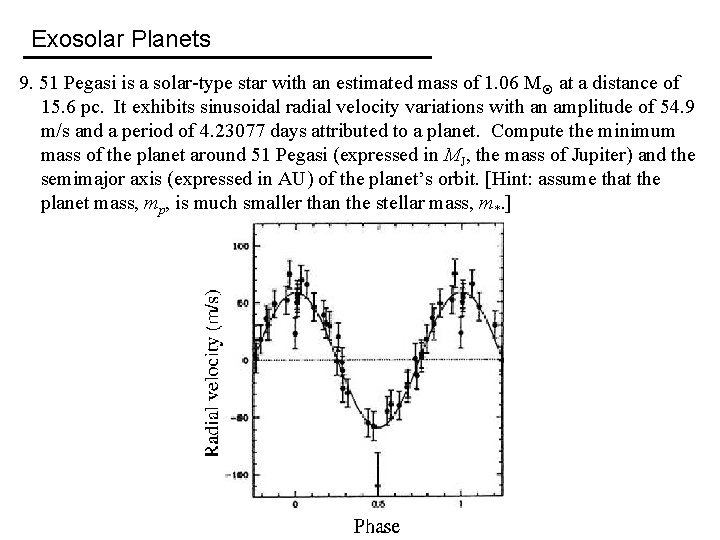
Exosolar Planets 9. 51 Pegasi is a solar-type star with an estimated mass of 1. 06 M at a distance of 15. 6 pc. It exhibits sinusoidal radial velocity variations with an amplitude of 54. 9 m/s and a period of 4. 23077 days attributed to a planet. Compute the minimum mass of the planet around 51 Pegasi (expressed in MJ, the mass of Jupiter) and the semimajor axis (expressed in AU) of the planet’s orbit. [Hint: assume that the planet mass, mp, is much smaller than the stellar mass, m*. ]

Exosolar Planets 9. 51 Pegasi is a solar-type star with an estimated mass of 1. 06 M at a distance of 15. 6 pc. It exhibits sinusoidal radial velocity variations with an amplitude of 54. 9 m/s and a period of 4. 23077 days attributed to a planet. Compute the minimum mass of the planet around 51 Pegasi (expressed in MJ, the mass of Jupiter) and the semimajor axis (expressed in AU) of the planet’s orbit. [Hint: assume that the planet mass, mp, is much smaller than the stellar mass, m*. ] Mass function, (mp sin i)3 / (m + mp)2 = (P/2πG) v r 3 * * (mp sin i)3 = (P/2πG) v r 3 (m + mp)2 * * Assuming mp << m * (mp sin i)3 ≅ 8. 6 × 1026 kg ≅ 0. 45 MJ mp ≥ 0. 45 MJ

Exosolar Planets 10. Would the precision of radial-velocity measurements have to be lower or higher for detecting a planet around a higher mass star, m*, for the same planet mass, mp, orbital inclination, i, orbital period, P, and orbital separation between the star and planet (assume a circular orbit)? Demonstrate your answer quantitatively: derive an expression for the radial velocity of the star, v*r, about the system’s center of mass in terms of the quantities given above and G, the Universal Gravitational constant. Kepler’s 3 rd law, P 2 = [4π2 a 3]/[G(m + m. P)] * = 4π2[P(v r + v. Pr)/(2π sin i)]3/[G(m + m. P)] * * Mass ratio m / m. P = v. Pr / v r so that * * P 2 = = 4π2[Pv r (1 + (m /m. P))/(2π sin i)]3/[G(m + m. P)] * * * i. e. , v r = 2π sin i [G/(4π2 P{m + m. P}2)]⅓ m. P * * Thus, for a given m. P, larger m* results in a smaller v r. *

Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the binary star system NSVS 01031772, in which data points for one star are indicated by circles and data points for the other star by squares. The lower panel of the figure below shows the optical light curves (in the V, R, and I bands) for the same system. The orbital period of the system is 0. 368141 days. (a) What is the approximate orbital eccentricity? Give reasons for your answer. b) Which star is more massive, the one indicated by circles or squares in the radial velocity curves? Give reasons for your answer. c) Which star is eclipsed at orbital phase 0. 5, the star with the higher or lower effective temperature? Give reasons for your answer. c) Compute, from the optical light curve in V, the ratio of the effective temperatures between the star having the higher and the star having the lower effective temperature. Note that a change in magnitude of Δm corresponds to a change in intensity of ΔF = 2. 512 -Δm.

Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the binary star system NSVS 01031772, in which data points for one star are indicated by circles and data points for the other star by squares. The lower panel of the figure below shows the optical light curves (in the V, R, and I bands) for the same system. The orbital period of the system is 0. 368141 days. (cont. ) e) What are the approximate radii (in units of R , the solar radius) of the two stars? Give full reasons for any assumptions made. e) What is the total mass (in units of M , the solar mass) of the binary system, pointing out any assumptions made. e) What are the masses (in units of M ) of the individual stars.

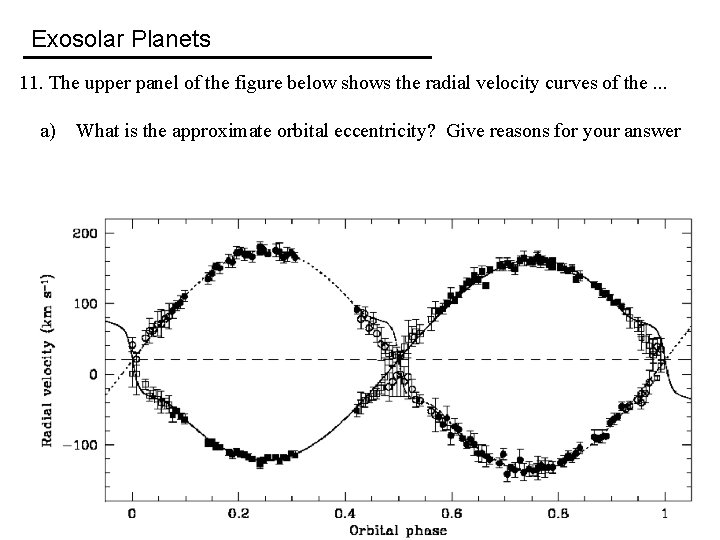
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . a) What is the approximate orbital eccentricity? Give reasons for your answer

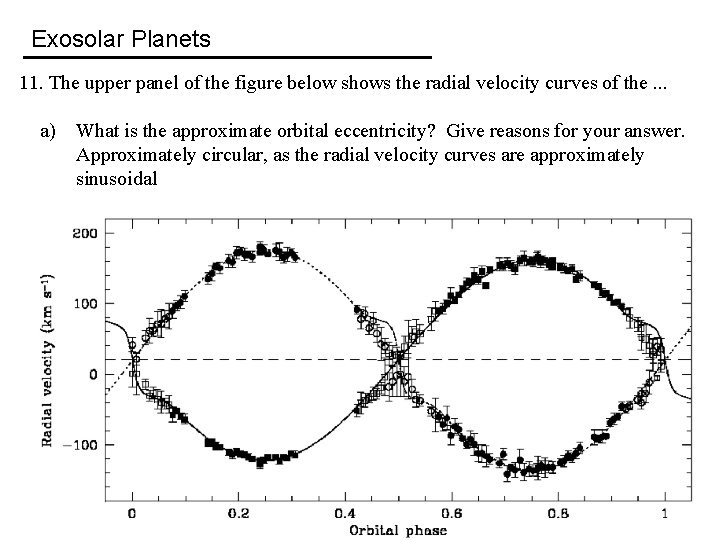
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . a) What is the approximate orbital eccentricity? Give reasons for your answer. Approximately circular, as the radial velocity curves are approximately sinusoidal

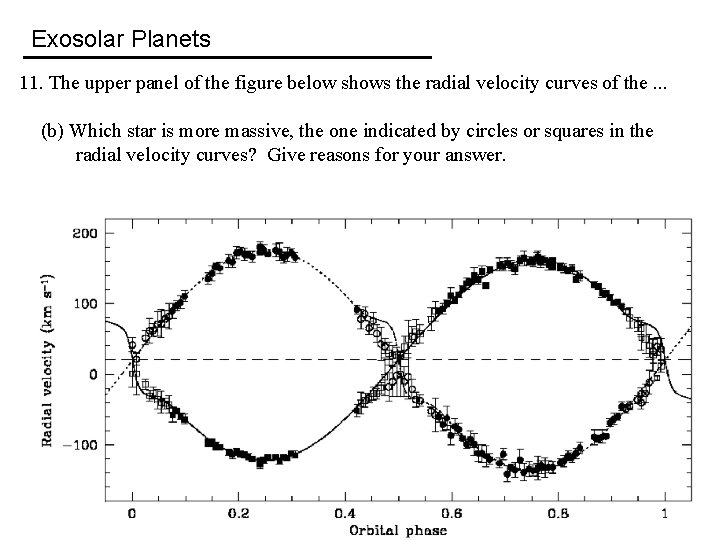
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (b) Which star is more massive, the one indicated by circles or squares in the radial velocity curves? Give reasons for your answer.

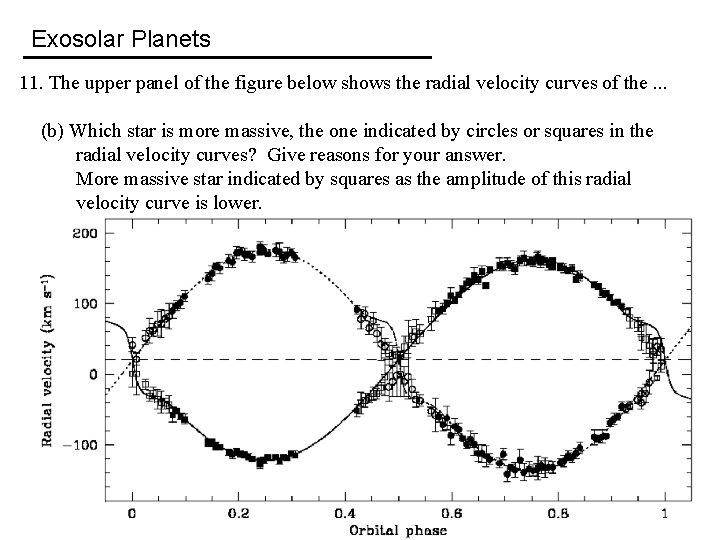
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (b) Which star is more massive, the one indicated by circles or squares in the radial velocity curves? Give reasons for your answer. More massive star indicated by squares as the amplitude of this radial velocity curve is lower.

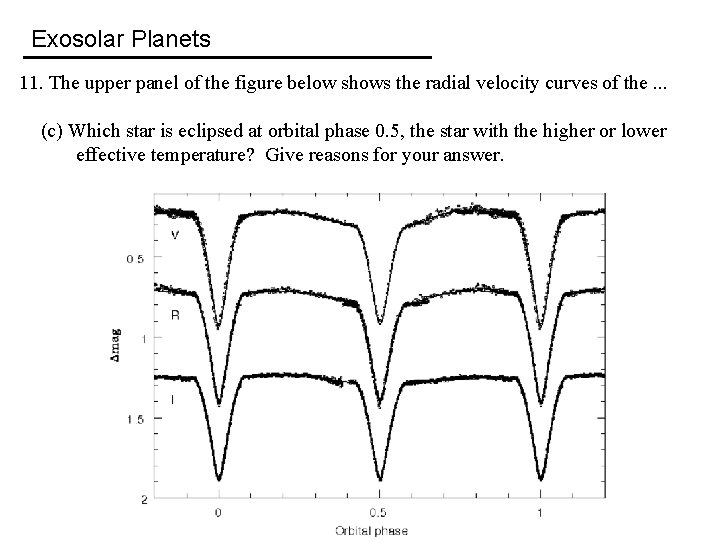
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (c) Which star is eclipsed at orbital phase 0. 5, the star with the higher or lower effective temperature? Give reasons for your answer.

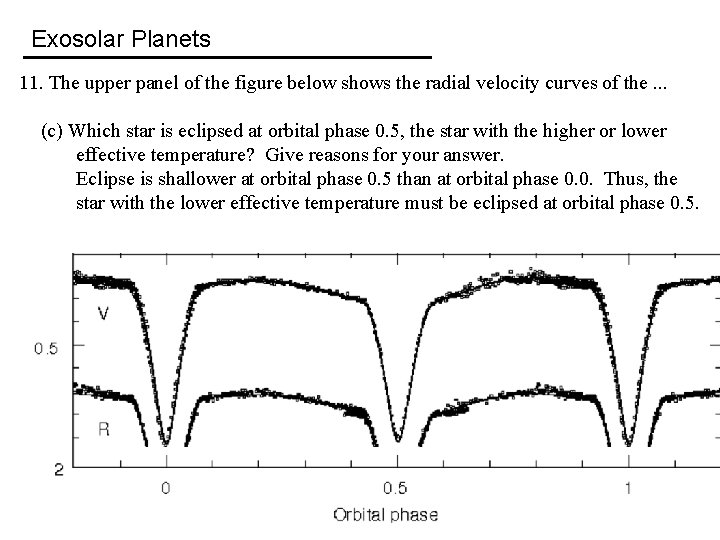
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (c) Which star is eclipsed at orbital phase 0. 5, the star with the higher or lower effective temperature? Give reasons for your answer. Eclipse is shallower at orbital phase 0. 5 than at orbital phase 0. 0. Thus, the star with the lower effective temperature must be eclipsed at orbital phase 0. 5.

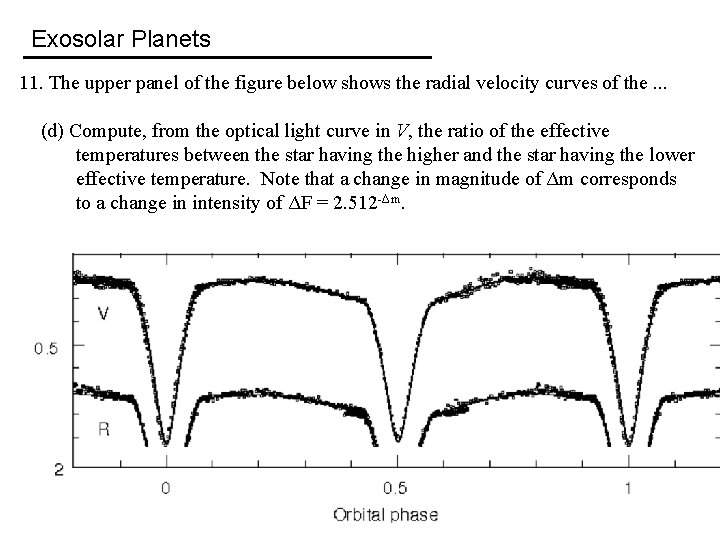
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (d) Compute, from the optical light curve in V, the ratio of the effective temperatures between the star having the higher and the star having the lower effective temperature. Note that a change in magnitude of Δm corresponds to a change in intensity of ΔF = 2. 512 -Δm.

Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (d) Compute, from the optical light curve in V, the ratio of the effective temperatures between the star having the higher and the star having the lower effective temperature. Note that a change in magnitude of Δm corresponds to a change in intensity of ΔF = 2. 512 -Δm. Now, Fp/Fs = (σTp 4)/(σTs 4), and so Tp/Ts = (Fp/Fs)1/4 = (ΔFp/ΔFs)1/4 = (1. 995/1. 906)1/4 = 1. 011.

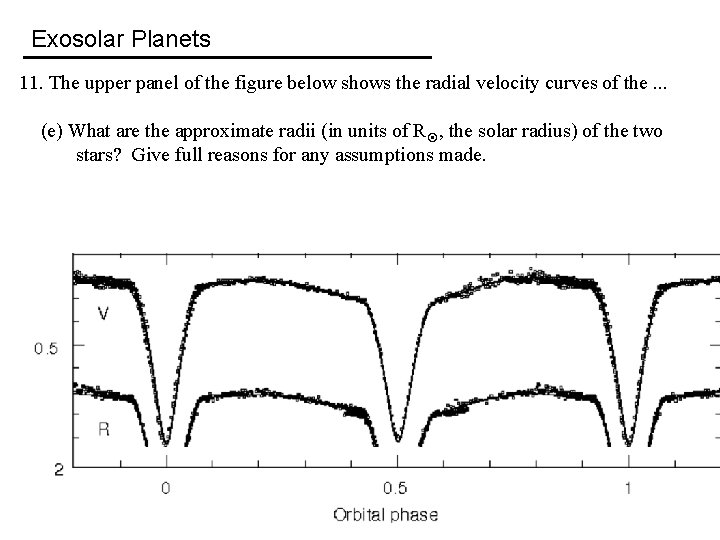
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (e) What are the approximate radii (in units of R , the solar radius) of the two stars? Give full reasons for any assumptions made.

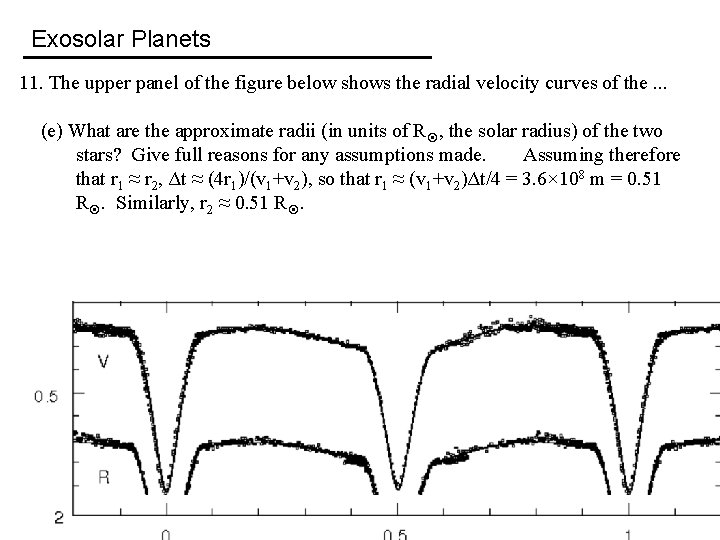
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (e) What are the approximate radii (in units of R , the solar radius) of the two stars? Give full reasons for any assumptions made. Assuming therefore that r 1 ≈ r 2, Δt ≈ (4 r 1)/(v 1+v 2), so that r 1 ≈ (v 1+v 2)Δt/4 = 3. 6× 108 m = 0. 51 R. Similarly, r 2 ≈ 0. 51 R.

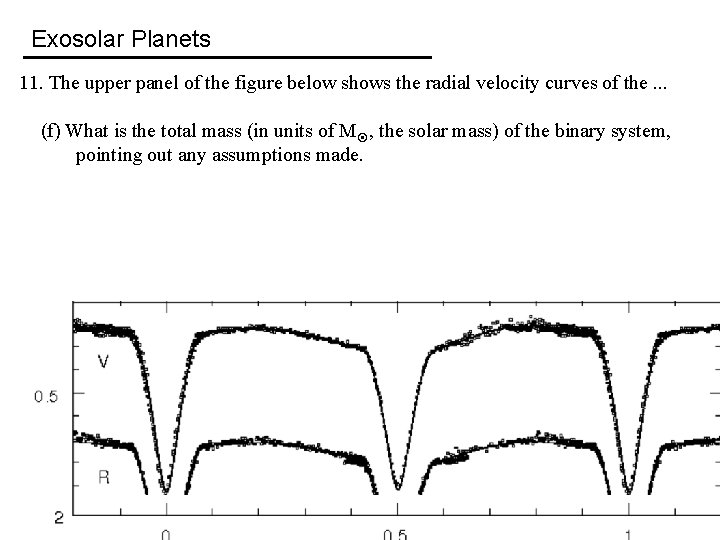
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (f) What is the total mass (in units of M , the solar mass) of the binary system, pointing out any assumptions made.

Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (f) What is the total mass (in units of M , the solar mass) of the binary system, pointing out any assumptions made. Total mass given by Kepler’s 3 rd law, From the radial velocity curve, v 1 ≈ 140 km/s and v 2 ≈ 160 km/s, so that (m 1+m 2) = 2. 05× 1030 kg = 1. 03 M.

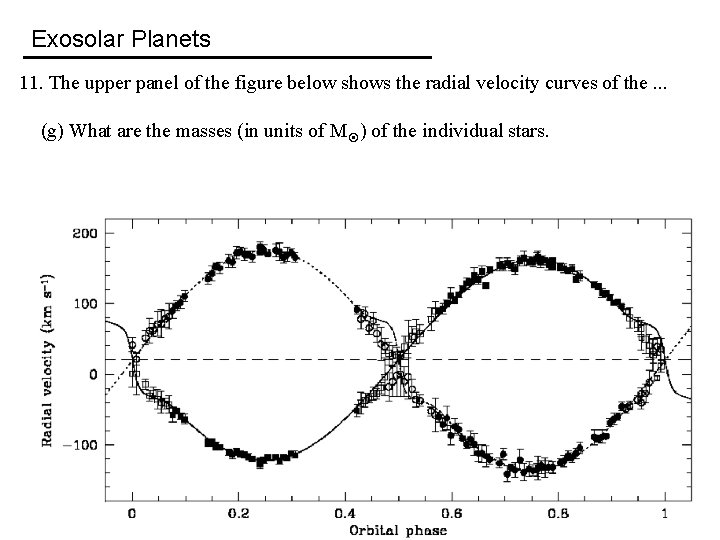
Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (g) What are the masses (in units of M ) of the individual stars.

Exosolar Planets 11. The upper panel of the figure below shows the radial velocity curves of the. . . (g) What are the masses (in units of M ) of the individual stars. From equation for center of mass, m 1 r 1+m 2 r 2 = m 1 a 1−m 2 a 2=0, m 1 = 16/30× 1. 03 M = 0. 55 M. Similarly, m 1+m 2 = 16/14 m 2+m 2 = 30/14 m 2 = 1. 03 M , so that m 2 = 14/30× 1. 03 M = 0. 48 M.

Eclipsing Spectroscopic Binaries 8. Note that there is an error in the question (figure). The computed radii and effective temperatures are inconsistent. [4/5/16 10: 08: 16 pm] Mandy Chen: if we keep the value of Ms and M 0, then Mp should be changed to 5. 66 [4/5/16 10: 08: 28 pm] Mandy Chen: and Ta/Tb will be 1. 6 (TA / TB)4 = 26. 8 TA / TB = 2. 3