REDOX Reactions Chapter 18 REDOX Reactions Oxidation number

REDOX Reactions Chapter 18

REDOX Reactions • Oxidation number - In order to keep track of electrons in chemical reactions, chemists assign an oxidation number to each element.

Determining Oxidation States • Oxidation number of an element in its native state is zero. • Alkali metals have an oxidation number of +1 • Alkaline earth elements have an oxidation number of +2 • The oxidation number of monatomic ions is the same as the charge.

Determining Oxidation States • Fluorine is 1 except for F 2. • Cl, Br, and I are 1 in binary compounds. • O is usually 2 (except for peroxides O 2 2 and superoxides O 2 1). • H is usually +1 (except for hydrides H 1) • The sum of the oxidation numbers equals the charge on ion or molecule.
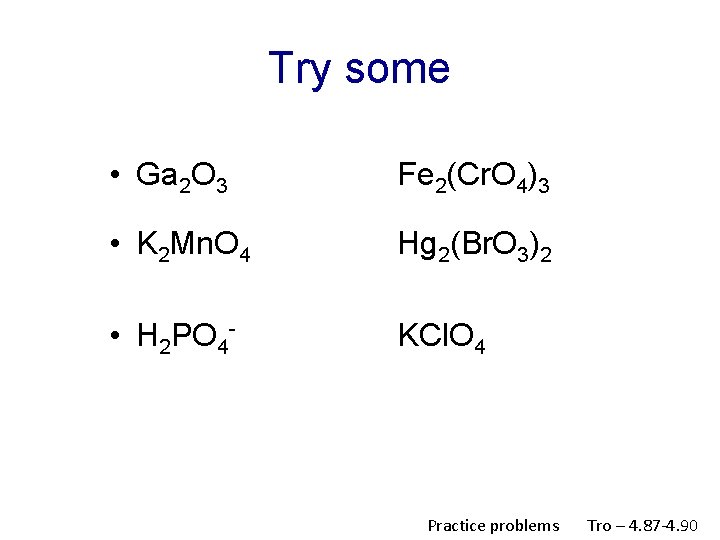
Try some • Ga 2 O 3 Fe 2(Cr. O 4)3 • K 2 Mn. O 4 Hg 2(Br. O 3)2 • H 2 PO 4 - KCl. O 4 Practice problems Tro – 4. 87 -4. 90

• Oxidation – process in which an element loses one or more electrons with an increase in the oxidation number. • Reduction – process in which an element gains one or more electrons with a decrease in oxidation number.

• Oxidizing agent – Substance that causes another substance to be oxidized. The oxidizing agent is always reduced. • Reducing agent – Substance that causes another substance to be reduced. The reducing agent is always oxidized.
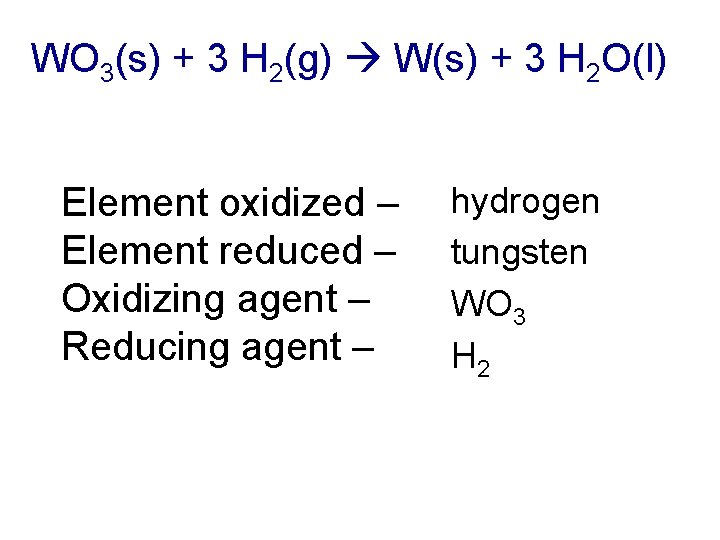
WO 3(s) + 3 H 2(g) W(s) + 3 H 2 O(l) Element oxidized – Element reduced – Oxidizing agent – Reducing agent – hydrogen tungsten WO 3 H 2

Sn. O 2(s) + 2 C(s) Sn(l) + 2 CO(g) Element oxidized – Element reduced – Oxidizing agent – Reducing agent – Carbon Tin Sn. O 2(s) C(s) Practice problems Tro – 4. 91 -4. 92

Half Reaction Method of Balancing Redox Reactions • Write skeleton ionic reaction. (Usually a given. ) • Split into 2 half reactions, one for oxidation and one for reduction. (Determine what is oxidized and what is reduced by calculating oxidation numbers. Remember LEO says GER Loses Electrons Oxidation, Gains Electrons Reduction)

Half Reaction Method of Balancing Redox Reactions • Balance each half reaction. – balance all but H and O. – balance O by adding H 2 O. – balance H by adding H+. – balance charge by adding electrons.

Half Reaction Method of Balancing Redox Reactions • Add half reactions together after multiplying by a factor to be sure electrons cancel.

Half Reaction Method of Balancing Redox Reactions • This method provides an equation for a reaction occurring in acid. To change to a balanced basic reaction add • H+ + OH H 2 O • to the reaction to cancel out all H+’s. Practice problems Tro – 18. 37 -18. 42

Balance in acid Cr 2 O 72 -(aq) + Cl-1(aq) Cr 3+(aq) + Cl 2(g) 14 H+(aq) + Cr 2 O 72 -(aq) + 6 Cl-1(aq) 2 Cr 3+(aq) + 3 Cl 2(g) + 7 H 2 O(l)

Balance in acid Mn. O 2(s) + Hg(l) + Cl-1(aq) Mn+2(aq) + Hg 2 Cl 2(s) 4 H+(aq) + Mn. O 2(s) + 2 Hg(l) + 2 Cl-1(aq) Mn+2(aq) + Hg 2 Cl 2(s) + 2 H 2 O(l)

Balance in acid Ag(s) + NO 3 -1(aq) Ag+1(aq) + NO(g) 4 H+(aq) + 3 Ag(s) + NO 3 -1(aq) 3 Ag+1(aq) + NO(g) + 2 H 2 O(l)

Balance in acid H 3 As. O 4(aq) + Zn(s) As. H 3(g) + Zn+2(aq) 8 H+(aq) + H 3 As. O 4(aq) + 4 Zn(s) As. H 3(g) + 4 Zn+2(aq) + 4 H 2 O(l)

Balance in acid Au+3(aq) + I 2(s) Au(s) + IO 3 -1(aq) 10 Au+3(aq) + 3 I 2(s) + 18 H 2 O(l) 36 H+(aq) + 10 Au(s) + 6 IO 3 -1(aq)

Balance in acid IO 3 -1(aq) + I-1(aq) I 3 -1(aq) 6 H+(aq) + IO 3 -1(aq) + 8 I-1(aq) 3 I 3 -1(aq) + 3 H 2 O(l) (Hint: if you divide the balanced equation by 3 you will get the result above. ) Balanced equation 18 H+(aq) +3 IO 3 -1(aq) + 24 I-1(aq) 9 I 3 -1(aq) + 9 H 2 O(l)

Balance in acid HS 2 O 3 -1(aq) S(s) + HSO 4 -1(aq) H+(aq) + 3 HS 2 O 3 -1(aq) 4 S(s) + 2 HSO 4 -1(aq) + H 2 O(l)

Balance in acid O 2 -2(aq) O 2(g) + H 2 O(l) 4 H+(aq) + 2 O 2 -2(aq) O 2(g) + 2 H 2 O(l)

Balance in acid Cr 2 O 7 -2(aq) + I 2(aq) Cr+3(aq) + IO 3 -1 34 H+(aq) + 5 Cr 2 O 7 -2(aq) + 3 I 2(aq) 10 Cr+3(aq) + 6 IO 3 -1 + 17 H 2 O(l)

Balance in acid S 2 O 3 -2(aq) + I 2(aq) S 4 O 6 -2(aq) + I-1(aq) 2 S 2 O 3 -2(aq) + I 2(aq) S 4 O 6 -2(aq) + 2 I-1(aq)

Balance in acid Mn. O 4 -1(aq) + H 2 O 2(aq) Mn+2(aq) + O 2(g) 6 H+(aq) + 2 Mn. O 4 -1(aq) + 5 H 2 O 2(aq) 2 Mn+2(aq) + 5 O 2(g) + 8 H 2 O(l)

Balance in acid Hg 2 Cl 2(s) + NO 2 -1(aq) Hg+2(aq) + NO(g) 4 H+(aq) + Hg 2 Cl 2(s) + 2 NO 2 -1(aq) 2 Hg+2(aq) + 2 NO(g) + 2 Cl-1(aq) +2 H 2 O(l)

Balance in acid Mn. O 4 -2(aq) Mn. O 2(s) + Mn. O 4 -1(aq) 4 H+(aq) + 3 Mn. O 4 -2(aq) Mn. O 2(s) + 2 Mn. O 4 -1(aq) + 2 H 2 O(l)

Balance in acid Pb(s) + Pb. O 2(s) + SO 4 -2(aq) Pb. SO 4(s) 4 H+(aq) + Pb(s) + Pb. O 2(s) + 2 SO 4 -2(aq) 2 Pb. SO 4(s) + 2 H 2 O(l)

Balance in base Co(OH)3(s) + Sn(s) Co(OH)2(s) + HSn. O 2 -1(aq) OH-1(aq) + 2 Co(OH)3(s) + Sn(s) 2 Co(OH)2(s) + HSn. O 2 -1(aq) + H 2 O(l)

Balance in base Cl. O 4 -1(aq) + I-1(aq) Cl. O 3 -1(aq) + IO 3 -1(aq) 3 Cl. O 4 -1(aq) + I-1(aq) 3 Cl. O 3 -1(aq) + IO 3 -1(aq)

Balance in base Pb. O 2(s) + Cl-1(aq) Cl. O-1(aq) + Pb(OH)3 -1(aq) OH-1(aq) + H 2 O(l) + Pb. O 2(s) + Cl-1(aq) Cl. O-1(aq) + Pb(OH)3 -1(aq)

Balance in base NO 2 -1(aq) + Al(s) NH 3(g) + Al. O 2 -1(aq) OH-1(aq) + H 2 O(l) + NO 2 -1(aq) + 2 Al(s) NH 3(g) + 2 Al. O 2 -1(aq)

Balance in base Cl. O-1(aq) Cl-1(aq) + O 2(g) 2 Cl. O-1(aq) 2 Cl-1(aq) + O 2(g)

Balance in base HXe. O 4 -1(aq) + Pb(s) Xe(g) + HPb. O 2 -1(aq) 2 OH-1(aq) + HXe. O 4 -1(aq) + 3 Pb(s) Xe(g) + 3 HPb. O 2 -1(aq)

Balance in base Ag 2 S(s) + CN-1(aq) + O 2(g) S(s) + Ag. CN(aq) 2 H 2 O(l) + 2 Ag 2 S(s) + 4 CN-1(aq) + O 2(g) 2 S(s) + 4 Ag. CN(aq) + 4 OH-1(aq)

Balance in base Mn. O 4 -1(aq) + S-2(aq) Mn. S(s) + S(s) 8 H 2 O(l) + 2 Mn. O 4 -1(aq) + 7 S-2(aq) 2 Mn. S(s) + 5 S(s) + 16 OH-1(aq)

Balance in base Cl 2(g) Cl. O-1(aq) + Cl-1(aq) 2 OH-1(aq) + Cl 2(g) Cl. O-1(aq) + Cl-1(aq) + H 2 O(l)
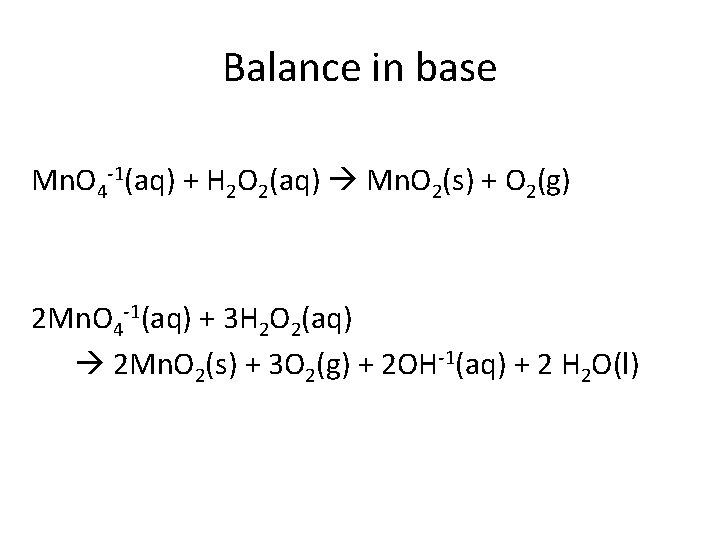
Balance in base Mn. O 4 -1(aq) + H 2 O 2(aq) Mn. O 2(s) + O 2(g) 2 Mn. O 4 -1(aq) + 3 H 2 O 2(aq) 2 Mn. O 2(s) + 3 O 2(g) + 2 OH-1(aq) + 2 H 2 O(l)

Balance in base Cl. O 2(aq) Cl. O 2 -1(aq) + Cl. O 3 -1(aq) 2 OH-1(aq) + 2 Cl. O 2(aq) Cl. O 2 -1(aq) + Cl. O 3 -1(aq) + H 2 O(l)

Balance in base Cr. O 4 -2(aq) + N 2 H 4(aq) Cr+3(aq) + N 2(g) 4 Cr. O 4 -2(aq) + 3 N 2 H 4(aq) + 4 H 2 O(l) 4 Cr+3(aq) + 3 N 2(g) + 20 OH-1(aq)

Balance in base Ag(s) + CN-1(aq) + O 2(g) Ag(CN)2 -1(aq) + OH-1(aq) 4 Ag(s) + 8 CN-1(aq) + O 2(g) + 2 H 2 O(l) 4 Ag(CN)2 -1(aq) + 4 OH-1(aq)

Balance in base Co(s) + Cl. O-1(aq) Co+2(aq) + Cl-1(aq) Co(s) + Cl. O-1(aq) + H 2 O(l) Co+2(aq) + Cl-1(aq) + 2 OH-(aq)

Balance in base Cd(s) + H 2 O(l) + Ni 2 O 3(s) Cd(OH)2(s) + Ni. O(s) Cd(s) + H 2 O(l) + Ni 2 O 3(s) Cd(OH)2(s) + 2 Ni. O(s)

• A vitamin C tablet was analyzed to determine whether it did in fact contain, as the manufacturer claimed, 1. 00 g of the vitamin. A tablet was dissolved in water to form a 100. 00 m. L solution, and a 10. 00 m. L sample was titrated with iodine (as KI 3, potassium triiodide). It required 10. 10 m. L of 0. 0521 M I 3 -1 to reach the stoichiometric point in the titration. Given that vitamin C, C 6 H 8 O 6, is oxidized to dehydroascorbic acid, C 6 H 6 O 6 and triiodide, I 3 -1, is reduced to iodide, I-1, write a balanced equation for the reaction and determine whether the manufacturer’s claim is correct? (MW vitamin C = 176 g/mol) Practice problems Tro – 18. 103 -18. 104, 18. 123
- Slides: 43