Redox Geochemistry Oxidation Reduction Reactions R E Oxidation

Redox Geochemistry

Oxidation – Reduction Reactions • • R E Oxidation - a process involving loss of electrons. Reduction - a process involving gain of electrons. Reductant - a species that loses electrons. Oxidant - a species that gains electrons. G s y a s • Free electrons do not exist in solution. Any electron lost from one species in solution must be immediately gained by another. Ox 1 + Red 2 Red 1 + Ox 2 L O E

Fundamental electromagnetic relations: • Electric charge (q) is measured in coulombs (C). – The magnitude of the charge of a single electron is 1. 602 x 10 -19 C. 1 mole of electrons has a charge of 9. 649 x 104 C which is called the Faraday constant (F) – q=n*F • The quantity of charge flowing each second through a circuit is called the current (i). The unit of current is the ampere (A) 1 A = 1 C/sec • The difference in electric potential (E) between two points is a measure of the work that is needed when an electric charge moves from one point to another. Potential difference is measured in volts (V) 1 V = 1 J/C – The greater the potential difference between two points, the stronger will be the "push" on a charged particle traveling between those points. A 12 V battery will push electrons through a circuit 8 times harder than a 1. 5 V battery. • Ohm’s Law: V = I R potential is equal to current * resistance

Half Reactions • Often split redox reactions in two: – oxidation half rxn e- leaves left, goes right • Fe 2+ Fe 3+ + e- – Reduction half rxn e- leaves left, goes right • O 2 + 4 e - 2 H 2 O • SUM of the half reactions yields the total redox reaction 4 Fe 2+ 4 Fe 3+ + 4 e. O 2 + 4 e - 2 H 2 O 4 Fe 2+ + O 2 4 Fe 3+ + 2 H 2 O

Examples Balance these and write the half reactions: • Mn(IV) + H 2 S Mn 2+ + S 0 + H+ • CH 2 O + O 2 CO 2 + H 2 O • H 2 S + O 2 S 8 + H 2 O

Redox Couples • For any half reaction, the oxidized/reduced pair is the redox couple: – Fe 2+ Fe 3+ + e– Couple: Fe 2+/Fe 3+ – H 2 S + 4 H 2 O SO 42 - + 10 H+ + 8 e– Couple: H 2 S/SO 42 -

Half-reaction vocabulary part II • Anodic Reaction – an oxidation reaction • Cathodic Reaction – a reduction reaction • Relates the direction of the half reaction: • A A+ + e- == anodic • B + e- B- == cathodic

ELECTRON ACTIVITY • Although no free electrons exist in solution, it is useful to define a quantity called the electron activity: • The pe indicates the tendency of a solution to donate or accept a proton. • If pe is low, there is a strong tendency for the solution to donate protons - the solution is reducing. • If pe is high, there is a strong tendency for the solution to accept protons - the solution is oxidizing.

THE pe OF A HALF REACTION - I Consider the half reaction Mn. O 2(s) + 4 H+ + 2 e- Mn 2+ + 2 H 2 O(l) The equilibrium constant is Solving for the electron activity

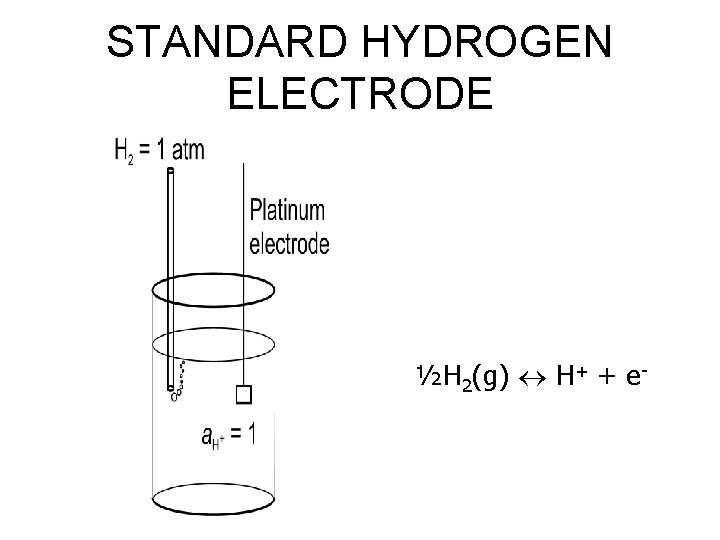
WE NEED A REFERENCE POINT! Values of pe are meaningless without a point of reference with which to compare. Such a point is provided by the following reaction: ½H 2(g) H+ + e. By convention so K = 1.

THE STANDARD HYDROGEN ELECTRODE If a cell were set up in the laboratory based on the half reaction ½H 2(g) H+ + eand the conditions a H+ = 1 (p. H = 0) and p H 2 = 1, it would be called the standard hydrogen electrode (SHE). If conditions are constant in the SHE, no reaction occurs, but if we connect it to another cell containing a different solution, electrons may flow and a reaction may occur.

STANDARD HYDROGEN ELECTRODE ½H 2(g) H+ + e-

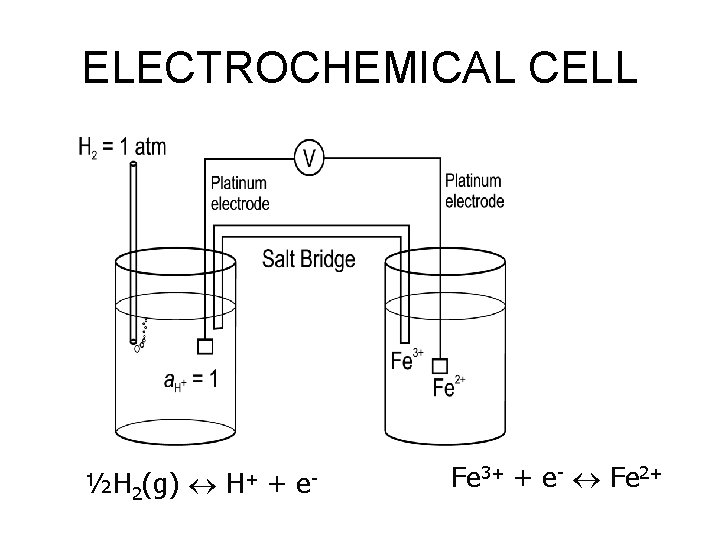
ELECTROCHEMICAL CELL ½H 2(g) H+ + e- Fe 3+ + e- Fe 2+

ELECTROCHEMICAL CELL We can calculate the pe of the cell on the right with respect to SHE using: If the activities of both iron species are equal, pe = 12. 8. If a Fe 2+/a Fe 3+ = 0. 05, then The electrochemical cell shown gives us a method of measuring the redox potential of an unknown solution vs. SHE.

DEFINITION OF Eh Eh - the potential of a solution relative to the SHE. Both pe and Eh measure essentially the same thing. They may be converted via the relationship: Where = 96. 42 k. J volt-1 eq-1 (Faraday’s constant). At 25°C, this becomes or

Free Energy and Electropotential • Talked about electropotential (aka emf, Eh) driving force for e- transfer • How does this relate to driving force for any reaction defined by DGr ? ? DGr = - n E – Where n is the # of e-’s in the rxn, is Faraday’s constant (23. 06 cal V-1), and E is electropotential (V) • pe for an electron transfer between a redox couple analagous to p. K between conjugate acid-base pair

Nernst Equation Consider the half reaction: NO 3 - + 10 H+ + 8 e- NH 4+ + 3 H 2 O(l) We can calculate the Eh if the activities of H+, NO 3 -, and NH 4+ are known. The general Nernst equation is The Nernst equation for this reaction at 25°C is

Eh – Measurement and meaning • Eh is the driving force for a redox reaction • No exposed live wires in natural systems (usually…) where does Eh come from? • From Nernst redox couples exist at some Eh (Fe 2+/Fe 3+=1, Eh = +0. 77 V) • When two redox species (like Fe 2+ and O 2) come together, they should react towards equilibrium • Total Eh of a solution is measure of that equilibrium

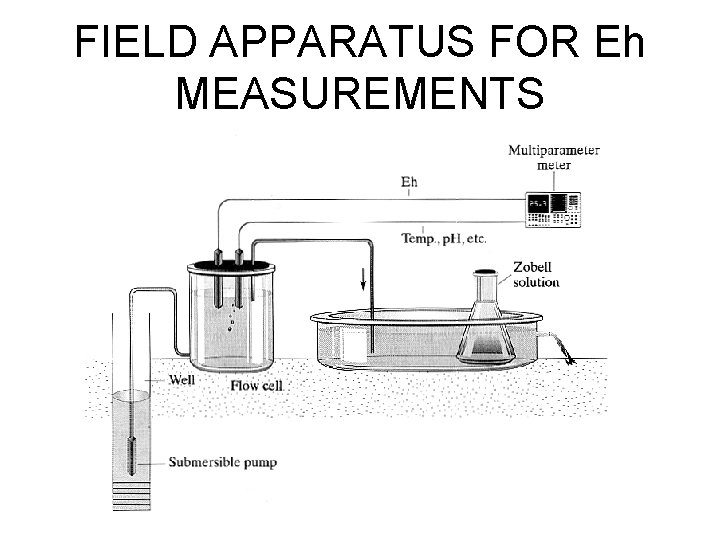
FIELD APPARATUS FOR Eh MEASUREMENTS

CALIBRATION OF ELECTRODES • The indicator electrode is usually platinum. • In practice, the SHE is not a convenient field reference electrode. • More convenient reference electrodes include saturated calomel (SCE - mercury in mercurous chloride solution) or silver-silver chloride electrodes. • A standard solution is employed to calibrate the electrode. • Zobell’s solution - solution of potassium ferric-ferro cyanide of known Eh.

CONVERTING ELECTRODE READING TO Eh Once a stable potential has been obtained, the reading can be converted to Eh using the equation Ehsys = Eobs + Eh. Zobell - Eh. Zobell-observed Ehsys = the Eh of the water sample. Eobs = the measured potential of the water sample relative to the reference electrode. Eh. Zobell = theoretical Eh of the Zobell solution Eh. Zobell = 0. 428 - 0. 0022 (t - 25) Eh. Zobell-observed = the measured potential of the Zobell solution relative to the reference electrode.

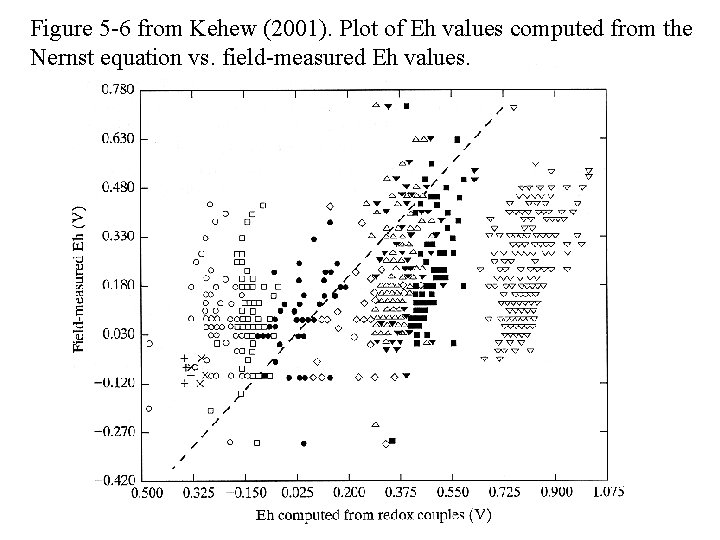
PROBLEMS WITH Eh MEASUREMENTS • Natural waters contain many redox couples NOT at equilibrium; it is not always clear to which couple (if any) the Eh electrode is responding. • Eh values calculated from redox couples often do not correlate with each other or directly measured Eh values. • Eh can change during sampling and measurement if caution is not exercised. • Electrode material (Pt usually used, others also used) – Many species are not electroactive (do NOT react electrode) • Many species of O, N, C, As, Se, and S are not electroactive at Pt – electrode can become poisoned by sulfide, etc.

Figure 5 -6 from Kehew (2001). Plot of Eh values computed from the Nernst equation vs. field-measured Eh values.

Other methods of determining the redox state of natural systems • For some, we can directly measure the redox couple (such as Fe 2+ and Fe 3+) • Techniques to directly measure redox SPECIES: – Amperometry (ion specific electrodes) – Voltammetry – Chromatography – Spectrophotometry/ colorimetry – EPR, NMR – Synchrotron based XANES, EXAFS, etc.

REDOX CLASSIFICATION OF NATURAL WATERS Oxic waters - waters that contain measurable dissolved oxygen. Suboxic waters - waters that lack measurable oxygen or sulfide, but do contain significant dissolved iron (> ~0. 1 mg L-1). Reducing waters (anoxic) - waters that contain both dissolved iron and sulfide.

Redox titrations • Imagine an oxic water being reduced to become an anoxic water • We can change the Eh of a solution by adding reductant or oxidant just like we can change p. H by adding an acid or base • Just as p. K determined which conjugate acid -base pair would buffer p. H, pe determines what redox pair will buffer Eh (and thus be reduced/oxidized themselves)

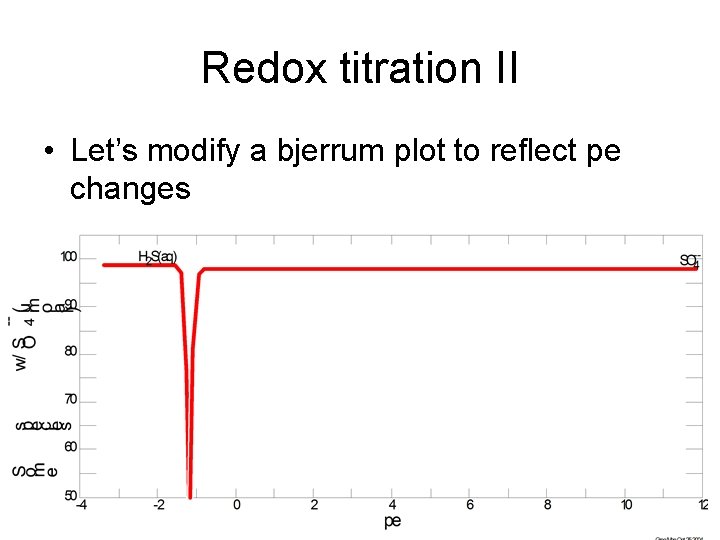
Redox titration II • Let’s modify a bjerrum plot to reflect pe changes

The Redox ladder O 2 Oxic H 2 O NO 3 - Post - oxic N 2 Mn. O 2 Mn 2+ Sulfidic Fe(OH)3 Fe 2+ SO 42 H 2 S Methanic CO 2 CH 4 H 2 O H 2 The redox-couples are shown on each stair-step, where the most energy is gained at the top step and the least at the bottom step. (Gibb’s free energy becomes more positive going down the steps)