Red Black trees Deliverables Red Black Tree Definition

Red Black trees

Deliverables Red Black Tree Definition Red Black Tree Insertion Red Black Tree Deletion Red Black Tree Analysis 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 2

Red Black trees It is a BST data structure with extra information in each node called the color field satisfying properties 1. Every Node is either red or black. 2. Root and leaves are all black. 3. Both children of every red node are black 4. All simple paths from node n to a descendent leaf of n has same number of black nodes called black height. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 3
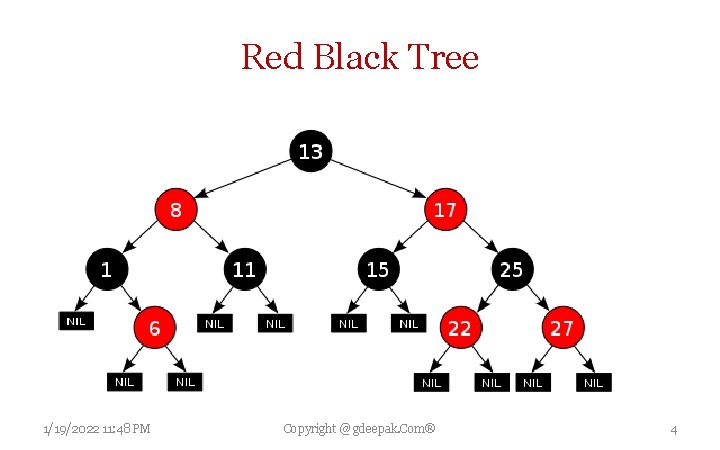
Red Black Tree 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 4

Height of the tree No path is more than twice as long as any other path. Consider the effect of properties 3 and 4 together. For a red black tree T, let B be the number of black nodes in property 4. Therefore the shortest possible path from the root of T to any leaf consists of B black nodes. Longer possible paths may be constructed by inserting red nodes. However, property 3 makes it impossible to insert more than one consecutive red node. Therefore the longest possible path consists of 2 B nodes, alternating black and red. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 5
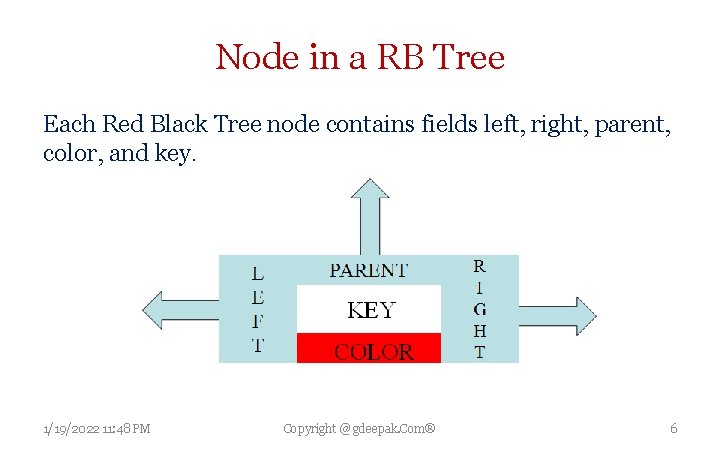
Node in a RB Tree Each Red Black Tree node contains fields left, right, parent, color, and key. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 6

RB tree Vs. 2 -3 -4 Tree Red black tree with n keys has height h≤ 2 lg(n+1). 2 -3 -4 trees are necessary to understand RB trees. 2 -4 Trees : All can have 1, 2 or 3 keys that means either 2 or 3 or 4 children except leaf which has no children. Depth of all leaves is same. The Height of 2 -4 tree is black height of RB tree created. Any 2 -4 tree can be converted to a red black tree and Vice versa. To convert RB Tree into 2 -4 tree Merge each red node into its black node. Now all leaves have same depth which is black height of root. To convert 2 -4 Tree into RB tree replace a node of 2 -4 tree with one black node and 0/1/2 red nodes which are children of black node. Height of 2 -4 tree is black height of RB tree created. Every red node has a black child 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 7
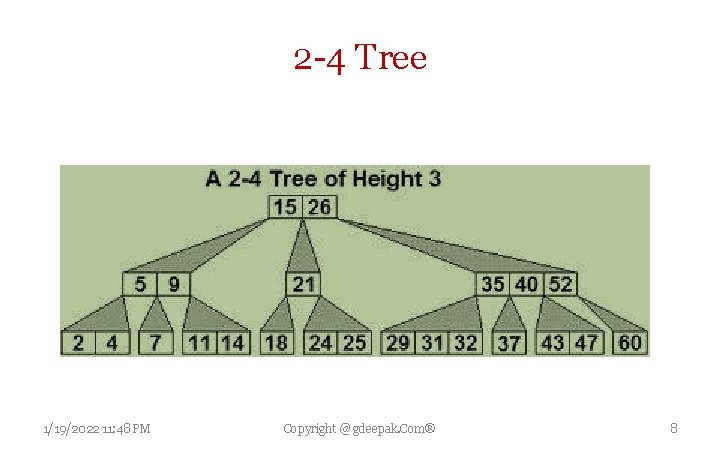
2 -4 Tree 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 8
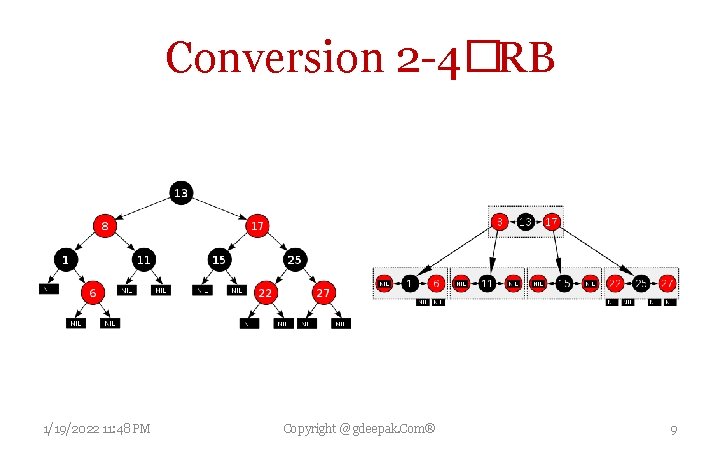
Conversion 2 -4�RB 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 9

Insertion in RB Tree Insertion begins by adding the node as BST insertion does and by colouring it red. Whereas in the binary search tree, we always add a leaf, in the RB tree leaves contain no information, so instead we add a red interior node, with two black leaves, in place of an existing black leaf. In case of insertion we will never have a black height problem and in case of deletion we will never have double red problem Case 1: The current node N is at the root of the tree. In this case, it is repainted black to satisfy Property 2 (The root is black). 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 10
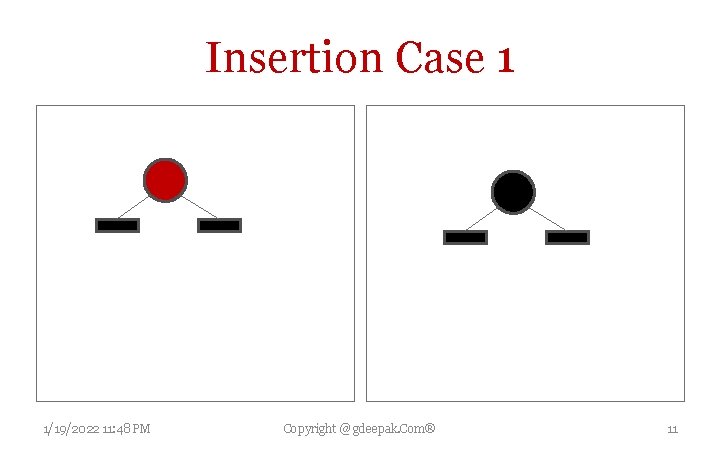
Insertion Case 1 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 11

Insertion Case 2 Current node's parent P is black, so Property 3 (Both children of every red node are black) is not invalidated. Property 4 is not threatened, because current node N has two black leaf children, but because N is red, the paths through each of its children have same number of black nodes as the path through the leaf it replaced, which was black, and so this property remains satisfied. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 12
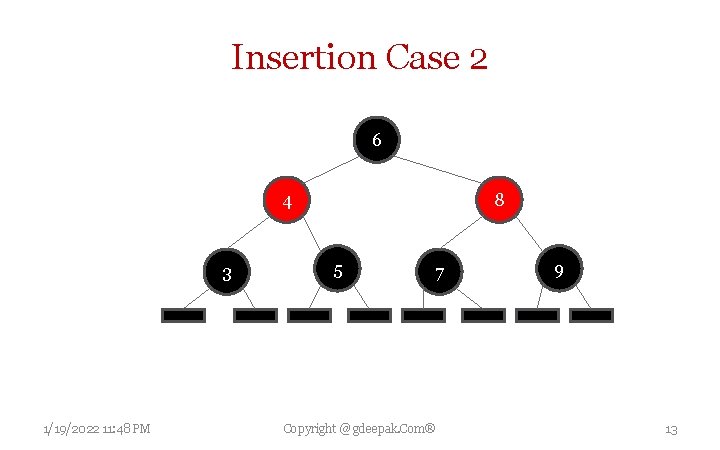
Insertion Case 2 6 4 3 1/19/2022 11: 48 PM 8 5 7 Copyright @ gdeepak. Com® 9 13
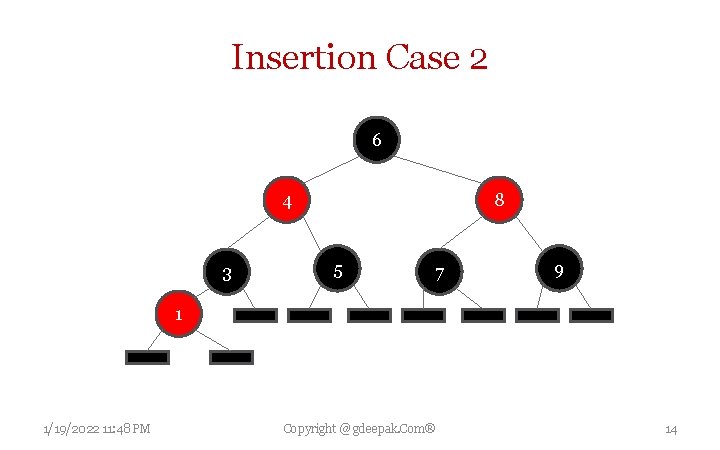
Insertion Case 2 6 4 3 8 5 7 9 1 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 14

Insertion Case 3 If both parent P and uncle U are red, then both of them can be repainted black and grandparent G becomes red (to maintain Property 4 (same black height)). Now, current red node N has a black parent. Since any path through parent or uncle must pass through the grandparent, the number of black nodes on these paths has not changed. However, grandparent G may now violate properties 2 (Root black) or 3 (Both children of red node are black) (property 3 possibly being violated since G may have a red parent). To fix this, the entire procedure is recursively performed on G from case 1. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 15
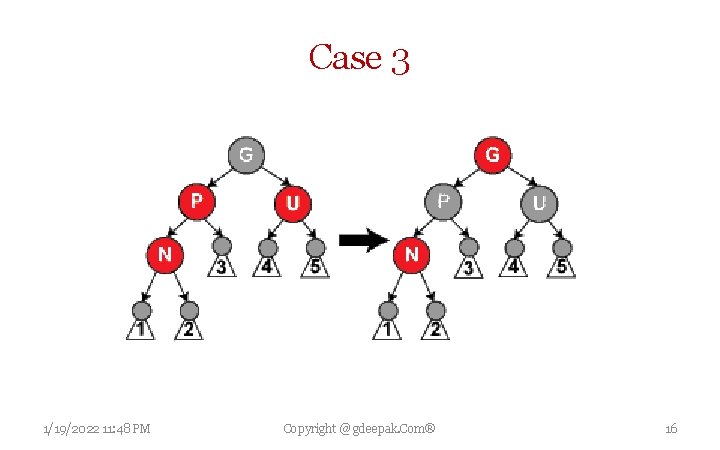
Case 3 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 16
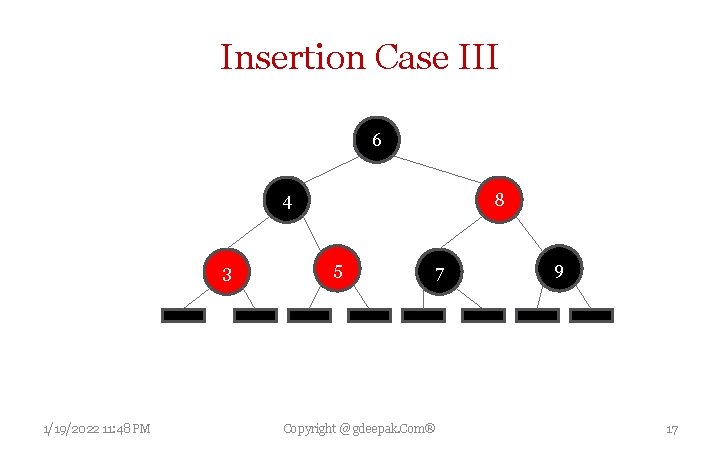
Insertion Case III 6 4 3 1/19/2022 11: 48 PM 8 5 7 Copyright @ gdeepak. Com® 9 17
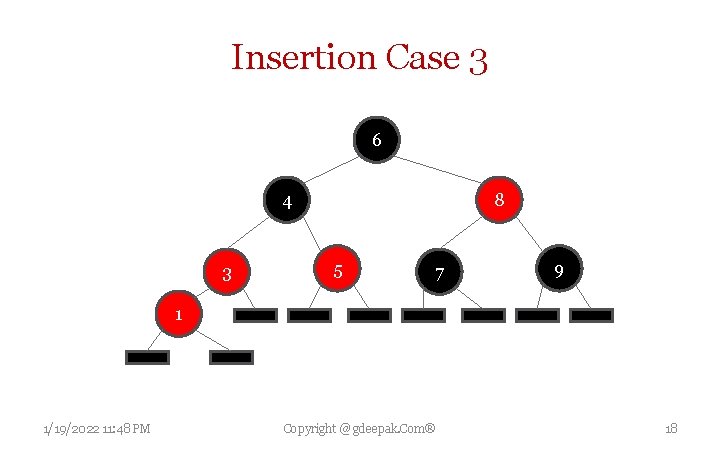
Insertion Case 3 6 4 3 8 5 7 9 1 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18
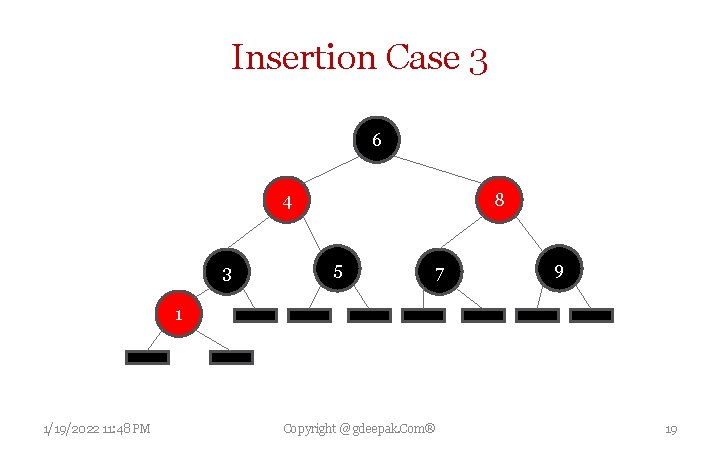
Insertion Case 3 6 4 3 8 5 7 9 1 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 19

Insertion Case 4 Parent P is red but uncle U is black; also current node N is right child of P, and P in turn is the left child of its parent G. so a left rotation that switches roles of current node N and its parent P can be performed; then, former parent node P is dealt with using Case 5 (relabeling N and P) because property 3 (children of red are black) is still violated. Rotation causes some paths (those in sub-tree labelled 1) to pass through node N where they did not before. It also causes some paths (those in the sub-tree labelled "3") not to pass through node P where they did before. However, both of these nodes are red, so Property 4 (All paths from any given node to its leaf nodes contain same number of black nodes) is not violated by rotation. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 20
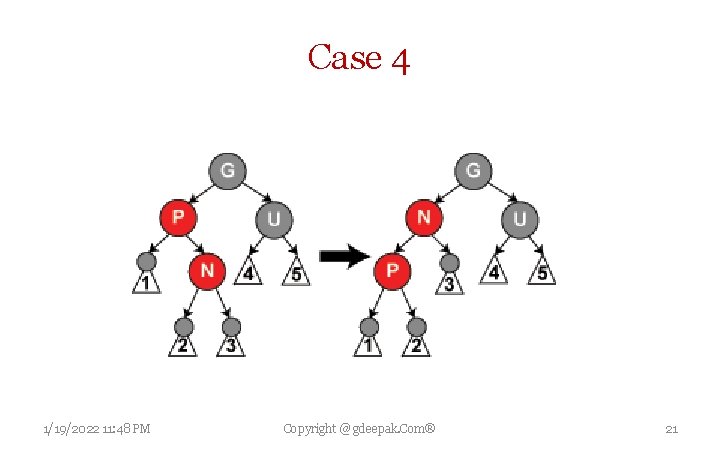
Case 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 21
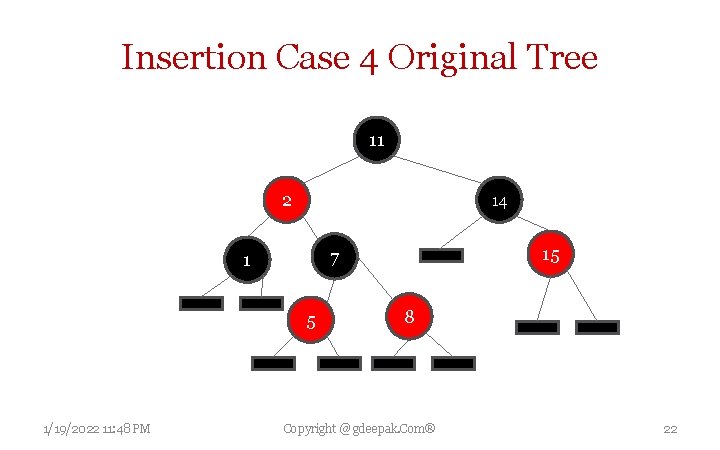
Insertion Case 4 Original Tree 11 2 14 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 22
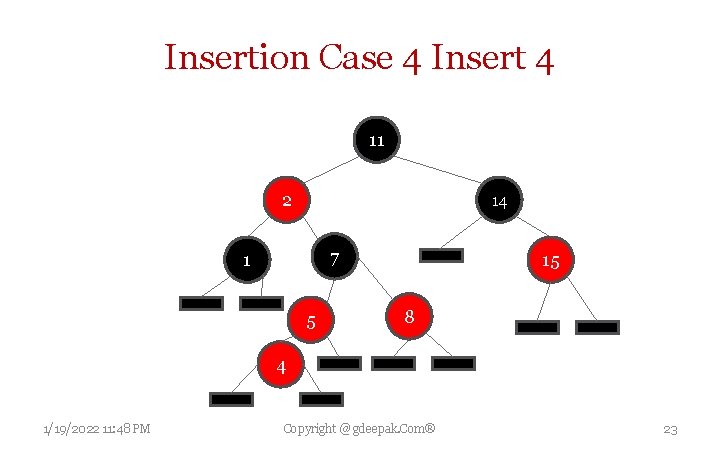
Insertion Case 4 Insert 4 11 2 14 7 1 5 15 8 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 23
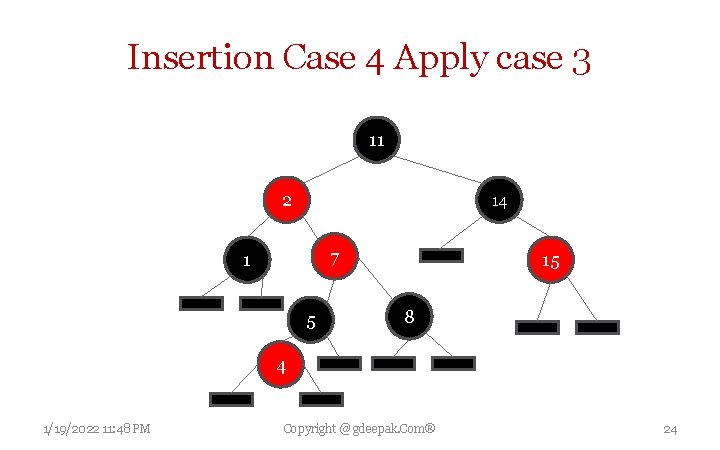
Insertion Case 4 Apply case 3 11 2 14 7 1 5 15 8 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 24
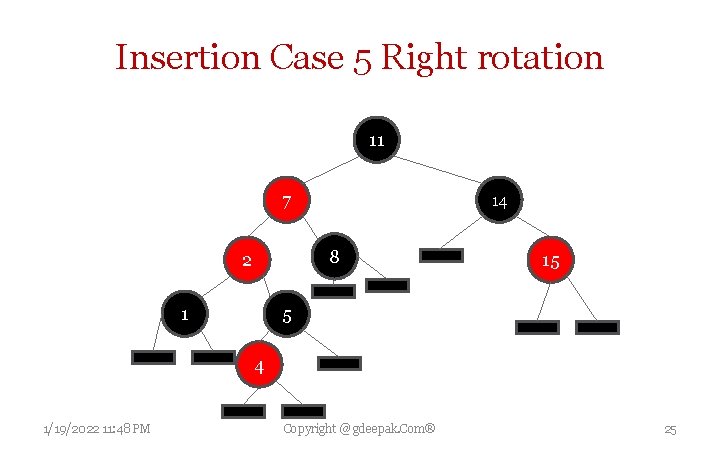
Insertion Case 5 Right rotation 11 7 14 8 2 1 15 5 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 25
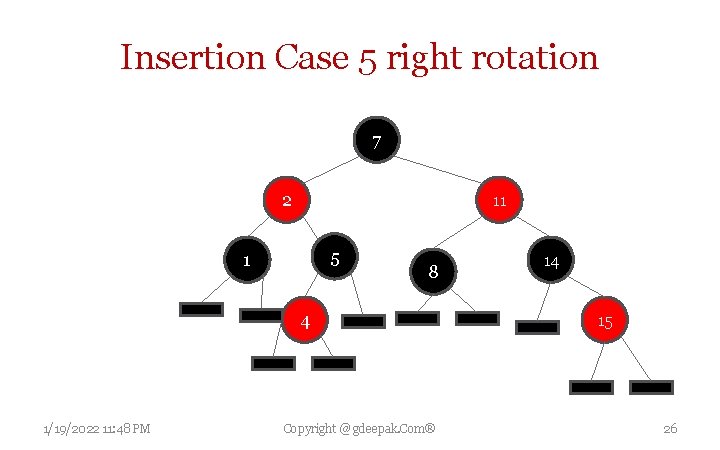
Insertion Case 5 right rotation 7 2 11 5 1 8 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 14 15 26

Insertion Case 5 The parent P is red but the uncle U is black, the current node N is the left child of P, and P is the left child of its parent G. In this case, a right rotation on G is performed; the result is a tree where the former parent P is now the parent of both the current node N and the former grandparent G. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 27
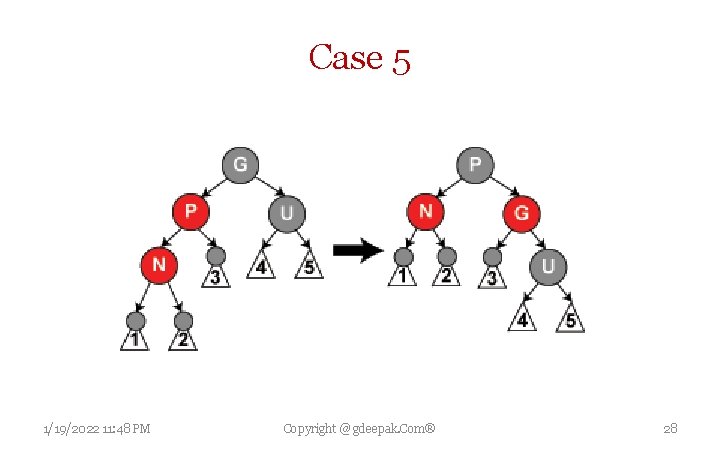
Case 5 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 28

Deletion In a regular binary search tree, when deleting a node with two non-leaf children, we find either maximum element in its left sub tree or minimum element in its right sub tree and move its value into the node being deleted. We then delete the node we copied the value from, which must have less than two non-leaf children. Because merely copying a value does not violate any red–black properties, this reduces to problem of deleting a node with at most one non-leaf child. Once we have solved that problem, solution applies equally to the case where the node we originally want to delete has at most one non-leaf child as to the case just considered where it has two non-leaf children. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 29

Case 1 When Element to be deleted is leaf node and it is Red, simple remove it. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 30
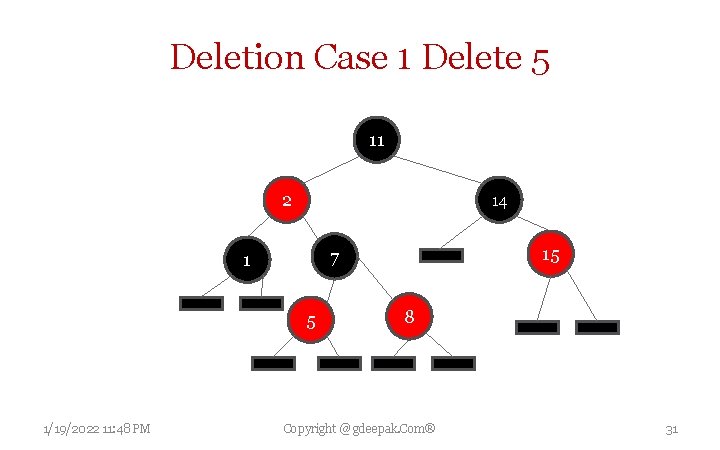
Deletion Case 1 Delete 5 11 2 14 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 31
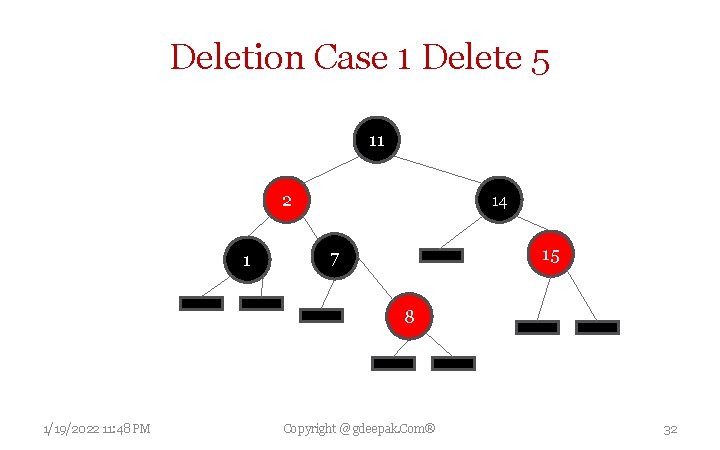
Deletion Case 1 Delete 5 11 2 1 14 15 7 8 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 32
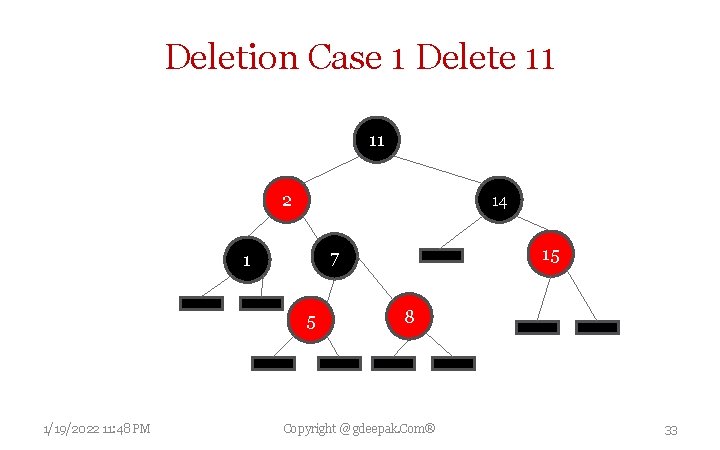
Deletion Case 1 Delete 11 11 2 14 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 33
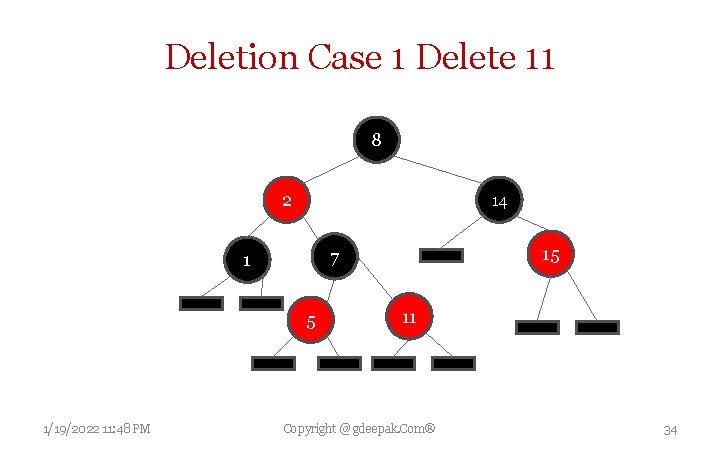
Deletion Case 1 Delete 11 8 2 14 5 1/19/2022 11: 48 PM 15 7 1 11 Copyright @ gdeepak. Com® 34
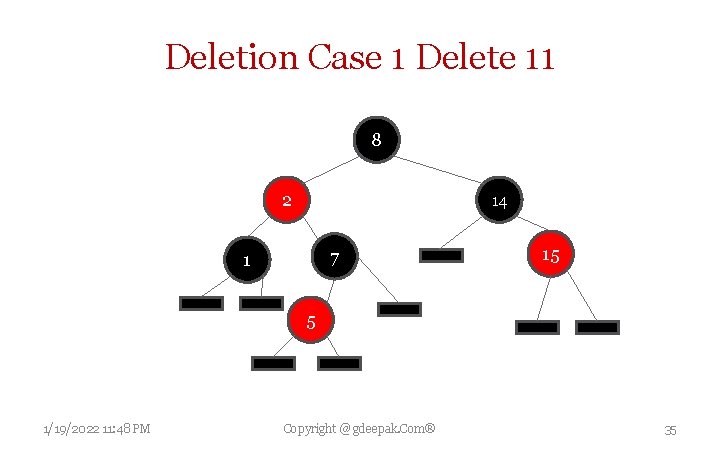
Deletion Case 1 Delete 11 8 2 14 7 1 15 5 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 35

Deletion Case 2 When parent is black and leaf child is Red, then replace the parent with the leaf and repaint the node with black. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 36
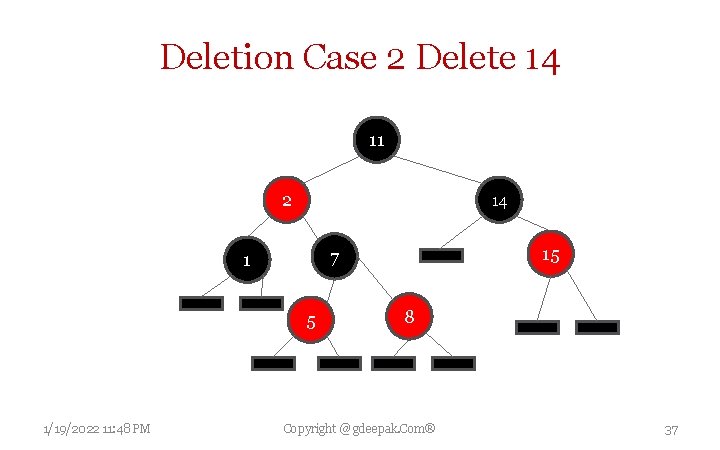
Deletion Case 2 Delete 14 11 2 14 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 37
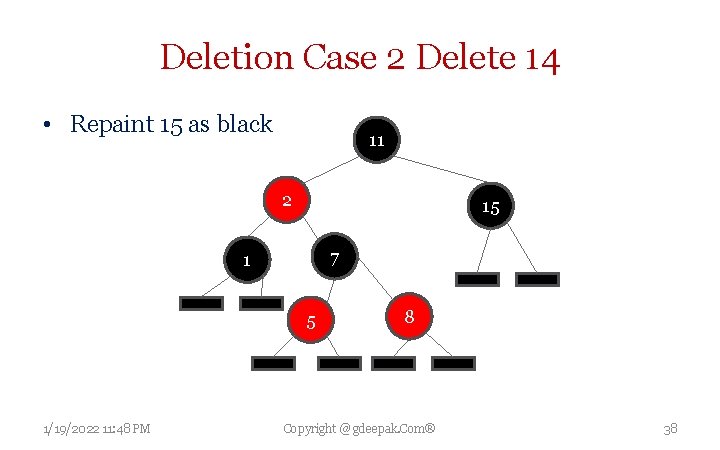
Deletion Case 2 Delete 14 • Repaint 15 as black 11 2 15 7 1 5 1/19/2022 11: 48 PM 8 Copyright @ gdeepak. Com® 38
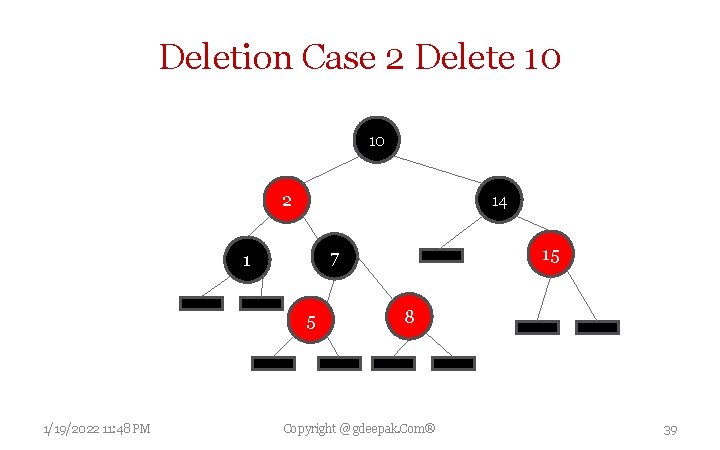
Deletion Case 2 Delete 10 10 2 14 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 39
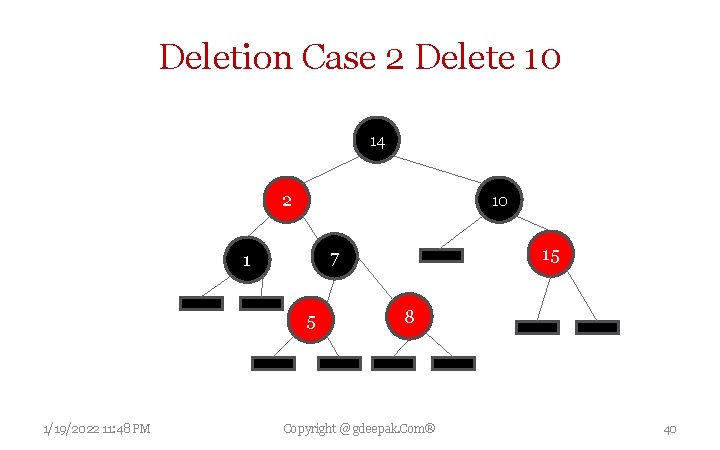
Deletion Case 2 Delete 10 14 2 10 5 1/19/2022 11: 48 PM 15 7 1 8 Copyright @ gdeepak. Com® 40
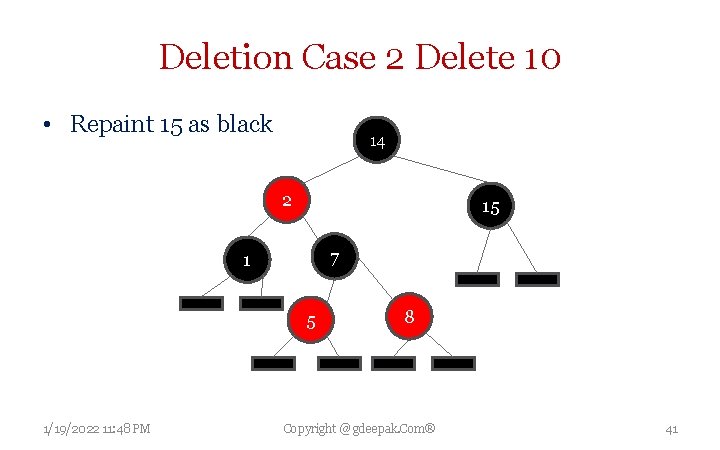
Deletion Case 2 Delete 10 • Repaint 15 as black 14 2 15 7 1 5 1/19/2022 11: 48 PM 8 Copyright @ gdeepak. Com® 41

Deletion Case 3 When parent is red and leaf is black. then it has to be two leaf nodes otherwise the black height would be different Both parent and leaf cannot be Red, because then it will not be valid RB tree So we are left with the option when both Parent and child are black, otherwise it will result in illegal RB tree. In this case we have to delete the leaf node which will result in decreasing the black height of that path by one. In this particular case of Black-Black we have 8 cases out of which 4 are similar to each other. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 42

Deletion BB case 1 Delete 2 • • • If x is the node to be deleted Sibling w is red and have black children Make sibling black and p[x] red Then left rotate on p[x] New sibling of x was a child of w before rotation so it must be black • Go to case 2, 3 or 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 43
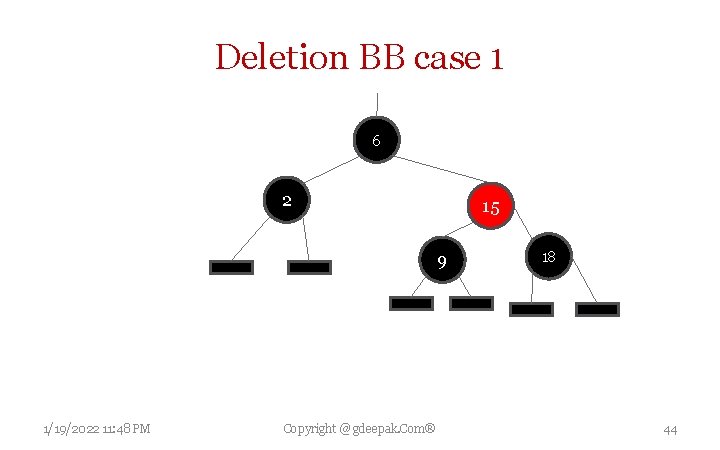
Deletion BB case 1 6 2 15 9 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18 44
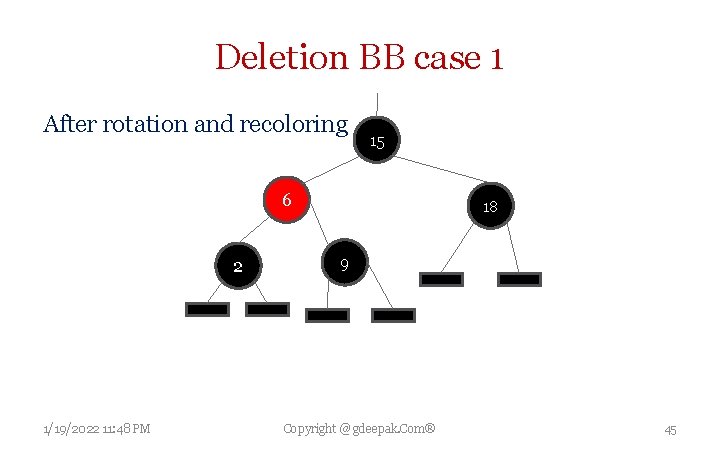
Deletion BB case 1 After rotation and recoloring 15 6 2 1/19/2022 11: 48 PM 18 9 Copyright @ gdeepak. Com® 45

Deletion BB case 2 • • W is black and both of w’s children are black Make x and w red Do the next iteration with p[x] as the new x If you had entered from case 1 then p[x] is red. Make this as black. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 46

Deletion BB case 2 6 2 15 9 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18 47
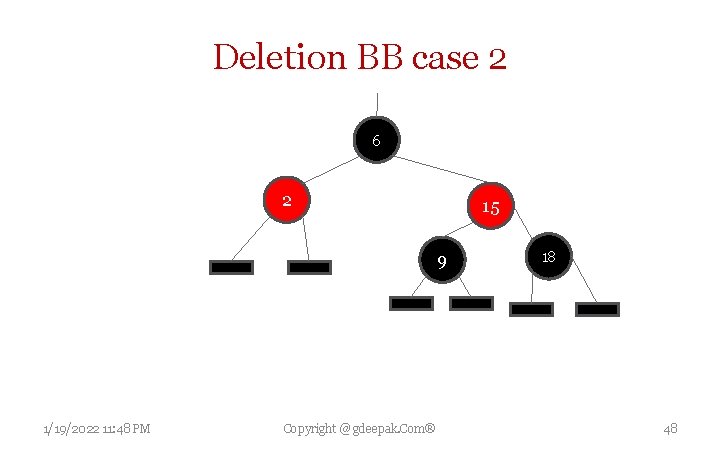
Deletion BB case 2 6 2 15 9 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18 48

Deletion BB case 3 • W is black w’s left child is red and w’s right child is black. • Make w red and w’s left child black. • Then right rotate on w • New sibling w of x is black with a red right child , go to case 4 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 49
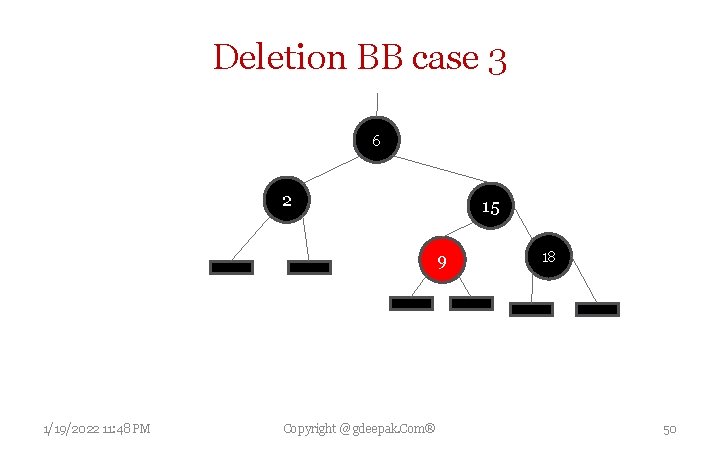
Deletion BB case 3 6 2 15 9 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18 50
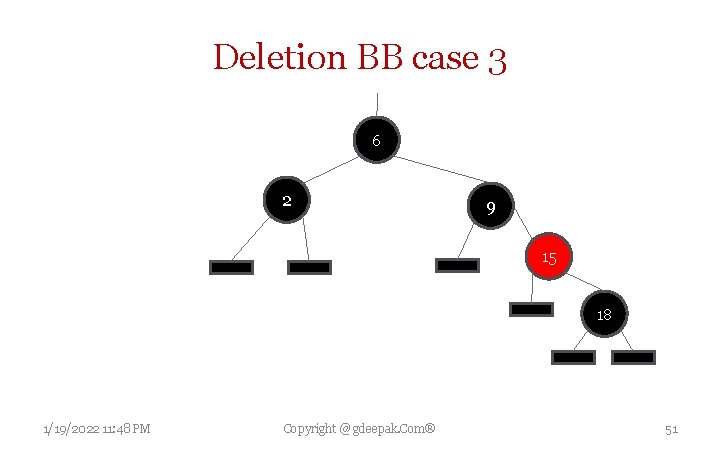
Deletion BB case 3 6 2 9 15 18 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 51

Deletion BB case 4 • W is black , w’s left child is black and right child is red • Make w as p[x]’s color • Make p[x] black and w’s right child black • Then left rotate on p[x] • Set x to root 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 52

Deletion BB case 4 6 2 15 9 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 18 53
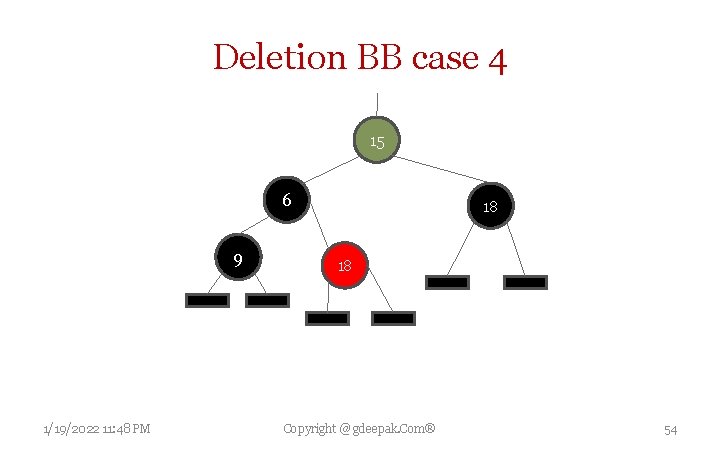
Deletion BB case 4 15 6 9 1/19/2022 11: 48 PM 18 18 Copyright @ gdeepak. Com® 54

AVL and RB trees AVL trees have average height 1. 44 * log(N+2) - 0. 33 Red Black trees have worst case height of 2. 00* log(N+1) Red Black & AVL trees both have O(log N) search, insert and delete, min, max, previous, next in terms of nodes. RB trees take O(log N) steps to find the correct place to insert. What is O(1) for Red Black insert, is any rebalancing necessary to restore the trees properties. At most a double left or right rotation is needed. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 55

AVL and RB Trees Deletion in AVL has rebalancing of O(log N). Here a RB tree gains over AVL. There is less rebalancing of nodes after an insert. RB trees have faster inserts and deletes than AVL at the expense of slower searches. AVL trees are rigidly balanced then RB trees so have slower insertion and deletion then RB trees but faster access. However For getting actual speed-up clean implementations are required, otherwise there are different arguments given for AVL vs. RB trees. 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 56

Questions, Comments and Suggestions 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 57

Question 1 What will be the result of deleting 12 from the RB tree. Node in bold is black and underlined is red. 30 / 15 / 12 1/19/2022 11: 48 PM / 20 35 45 Copyright @ gdeepak. Com® 60 58

Question 2 Show result of inserting 50 into RB tree. Node in bold is black and underlined is red. 30 / 15 45 / 35 60 / 55 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 59

Question 3 What is the maximum height of a Red-Black Tree with 14 nodes? Draw the tree with 14 nodes 10, 20, 30, 45, 50, 55, 60, 70, 83, 85, 90, 95 1/19/2022 11: 48 PM Copyright @ gdeepak. Com® 60
- Slides: 60