Recursive Methods for Finding Roots of Functions Bisection

Recursive Methods for Finding Roots of Functions Bisection & Newton’s Method

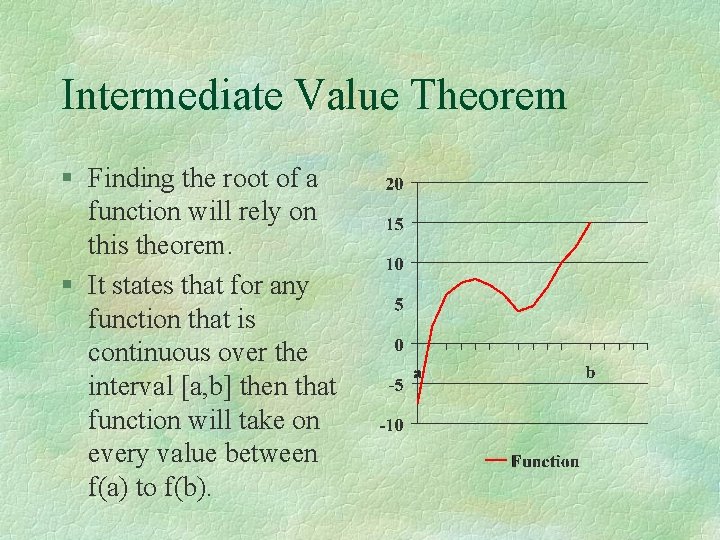
Intermediate Value Theorem § Finding the root of a function will rely on this theorem. § It states that for any function that is continuous over the interval [a, b] then that function will take on every value between f(a) to f(b).

BISECTION § Bisection requires narrowing one root onto a certain interval [a, b] § Testing this interval in the function f should give values which are opposite in sign for f(a) and f(b). § Bisecting this interval and testing f((a+b)/2) will yield another smaller interval in which to continue bisecting until the desired accuracy is reached.

Bisection Example Given to an accuracy of 10^-3. , find the root between 2 and 3 § 1 st Compare: f(2) = -1 and f(3) = 16. By the Intermediate Value Theorem we are insured that at least one root exists between 2 and 3. § 2 nd Test f((2+3)/2) = f(2. 5). All we need to know is it’s sign. It is positive. § 3 rd, we narrow our search interval from [2, 3] to [2, 2. 5] since f(2) is negative and f(2. 5) is positive.

Bisection Example § Continuing this pattern to finish the problem: iteration 2: f(2. 25)>0, new interval: [2, 2. 25] iteration 3: f(2. 125)>0, new interval: [2, 2. 125] iteration 4: f(2. 0625)<0, new interval: [2. 0625, 2. 125] iteration 5: f(2. 09375)<0, new interval: [2. 09375, 2. 125] iteration 6: f(2. 109375)>0, new interval: [2. 09375, 2. 109375] iteration 7: f(2. 1015625)>0, new int: [2. 09375, 2. 1015625] iteration 8: f(2. 09765625)>0, new int: [2. 09375, 2. 09765625] iteration 9: f(2. 095703125)>0, int: [2. 09375, 2. 095703125] Root approximation is the midpoint of this interval: x=2. 094390625

Bisection Example § We stop at this point because the desired accuracy has been reached. § The root is always as accurate as half of the interval arrived at, or in this case: (2. 09503125 -2. 09375)/2 =. 0009765625

Bisection Accuracy § Accuracy is always arrived at by taking half the current interval because the actual root could be no farther than that away from the midpoint. § The initial accuracy of the midpoint is: |ba|/2 § After each iteration, this accuracy is halved. § After n iterations accuracy is: |b-a|/2^(n+1)

Psuedocode Input function, interval where root exists, and desired accuracy. {f, a, b, E} n=1 While E > |b - a| / 2^n g = (b + a) / 2 //make a guess for root at midpoint if f(g) is the same sign as b then b = g else a = g endif n=n+1 End loop Display guess as g to accuracy of |b - a| / 2^n

NEWTON’S METHOD § Requires you to make a relatively good guess for the root of f(x), x 0. § Construct a tangent line to f(x) at this point: y - f(x 0) = f´(x 0)(x - x 0) § Find the x-intercept of this line (y = 0): 0 - f(x 0) = f´(x 0)(x - x 0) OR x = x 0 - f(x 0) / f´(x 0) § Repeat guess for this new x.

Newton’s Method Example Given to an accuracy of 10^-3. , find the root between 2 and 3 § 1 st Guess: By view the graph make an initial guess of x 0 = 2. § 2 nd find new x: x 1 = 2 - f(2) / f´(2) = 2. 1 § 3 rd repeat for x = 2. 1

Newton’s Method Example § Continuing this pattern takes much less time to narrow down than bisection: iteration 2: x 2 = 2. 1 - f(2. 1) / f´(2. 1) = 2. 0945681211 iteration 3: x 3 = x 2 - f(x 2) / f´(x 2) = 2. 0945514817 § You can already see that by the third iteration the accuracy of the root is to 0. 0000166394 or less than 10^-3. § The number of iterations will depend on how good your guess is.

Psuedocode Input function, guess, and desired accuracy. {f, g, E} n=0 While |gn - gn-1| > E n=n+1 gn = gn-1 - f(gn-1) / f´(gn-1) End loop Display root as gn to accuracy of |gn - gn-1|

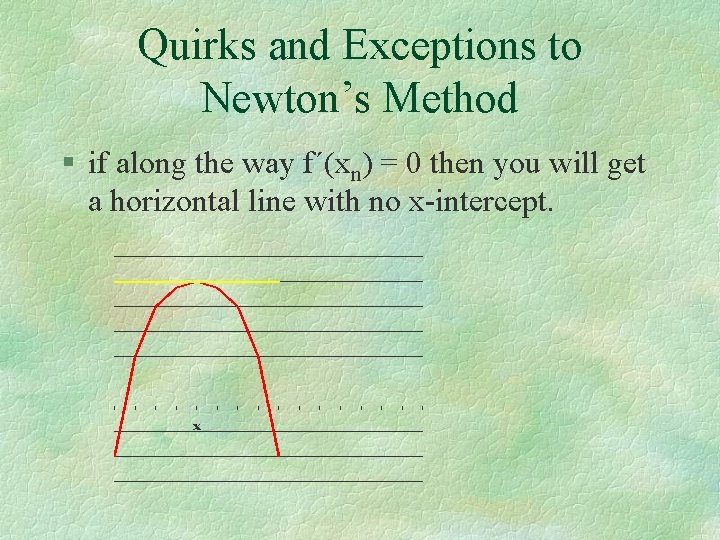
Quirks and Exceptions to Newton’s Method § if along the way f´(xn) = 0 then you will get a horizontal line with no x-intercept.

Quirks and Exceptions to Newton’s Method § You may get the wrong root depending on your initial guess. x 0 x 1

Quirks and Exceptions to Newton’s Method § You may get the wrong root. x 0 x 1