Recursive MATLAB program for building the Pythagoras Tree

Recursive MATLAB program for building the Pythagoras Tree Alexander Rozhok, IAN-103
Figure overview

Traditional Pythagoras Tree

Total area remains the same for each level 0. 125 0. 25 0. 5 1 0. 125

Pythagoras Tree variations with different angles of inclination

MATLAB implementation

Function header function my. Pythagoras(angle, iterations) α
![Main function body fill([-1 -1 1 1], [-1 1 1 -1], [0. 3671875 0. Main function body fill([-1 -1 1 1], [-1 1 1 -1], [0. 3671875 0.](http://slidetodoc.com/presentation_image/1741945ecbbdb64f5c813e25684853e9/image-8.jpg)
Main function body fill([-1 -1 1 1], [-1 1 1 -1], [0. 3671875 0. 2265625 0. 08984375]); %Draw seeding square axis equal; hold on; build. Squares([-1 1], [1 1], angle, 1); %Pass seeding square to the recursive func hold off;
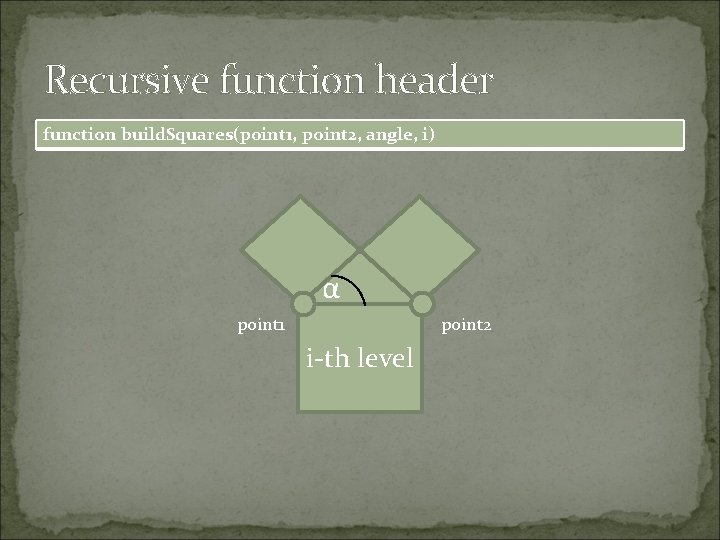
Recursive function header function build. Squares(point 1, point 2, angle, i) α point 1 point 2 i-th level

Recursion depth control if (i > iterations) return end

Finding the triangle vertex dir. Vector = point 2 - point 1; perp. Vector = [-dir. Vector(2) dir. Vector(1)]. / 2; angle 2 = pi / 2 - angle; side = norm(perp. Vector) * tan(angle 2); side. Vector = side. * dir. Vector. / norm(dir. Vector); pcenter = point 1 + side. Vector + perp. Vector; pcenter α point 1 dir. Vector i-th level point 2 Our goal is to find the coordinates of pcenter so we would be able to build new squares
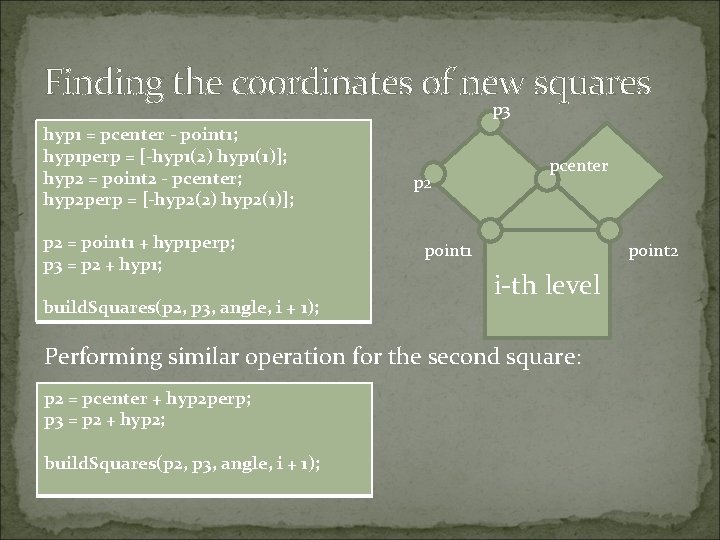
Finding the coordinates of new squares p 3 hyp 1 = pcenter - point 1; hyp 1 perp = [-hyp 1(2) hyp 1(1)]; hyp 2 = point 2 - pcenter; hyp 2 perp = [-hyp 2(2) hyp 2(1)]; p 2 = point 1 + hyp 1 perp; p 3 = p 2 + hyp 1; build. Squares(p 2, p 3, angle, i + 1); p 2 pcenter point 1 point 2 i-th level Performing similar operation for the second square: p 2 = pcenter + hyp 2 perp; p 3 = p 2 + hyp 2; build. Squares(p 2, p 3, angle, i + 1);
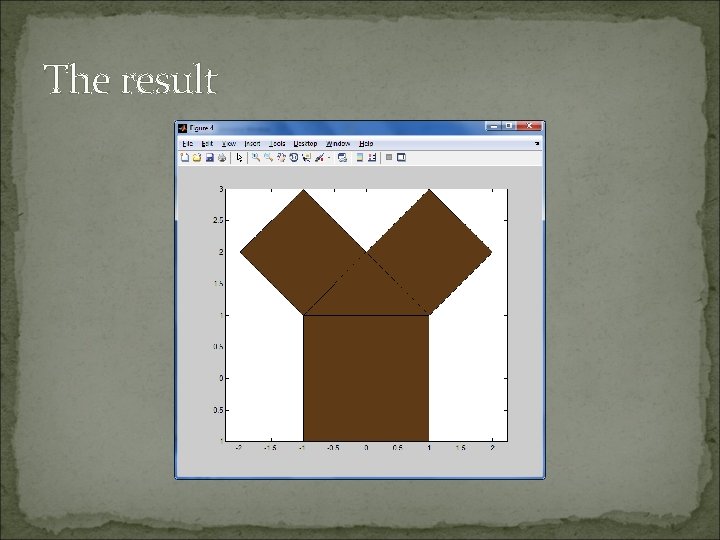
The result
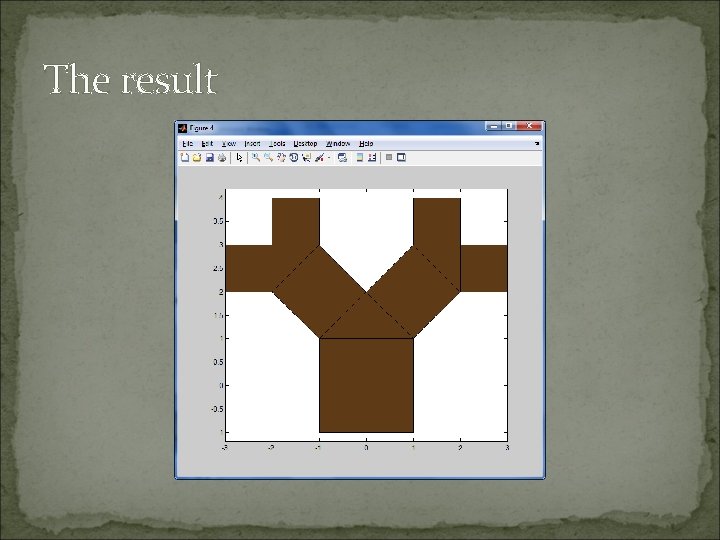
The result
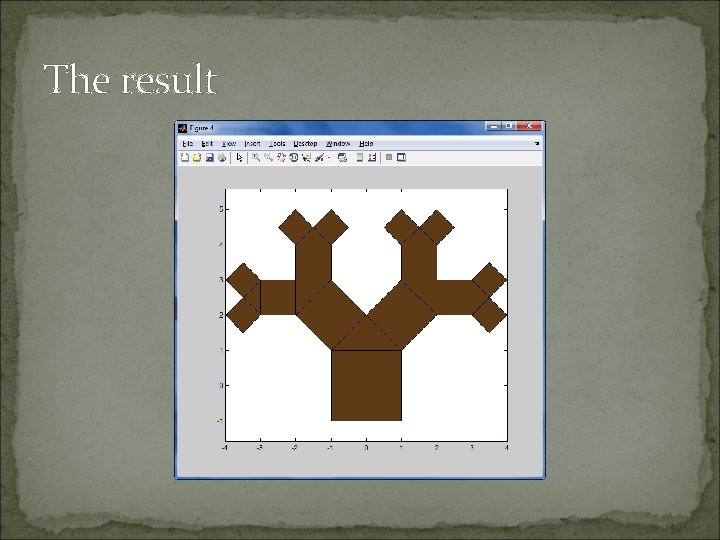
The result
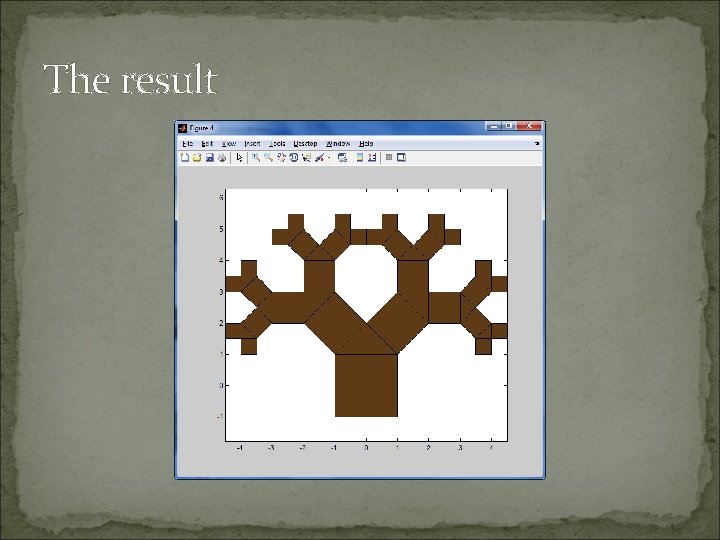
The result
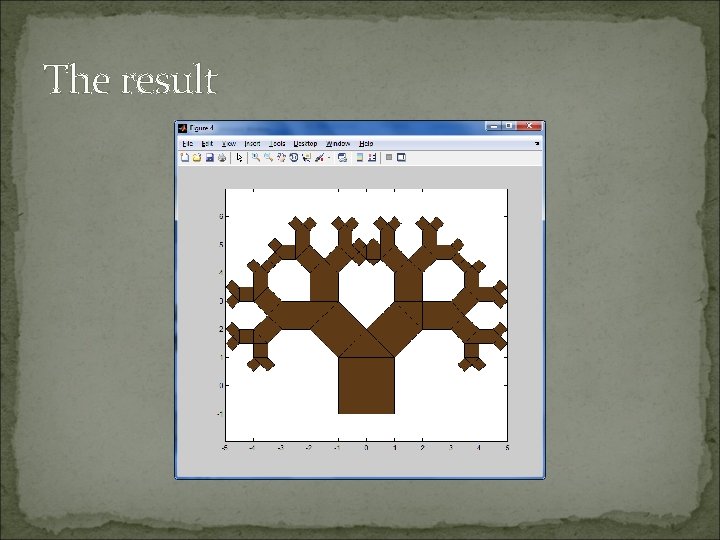
The result
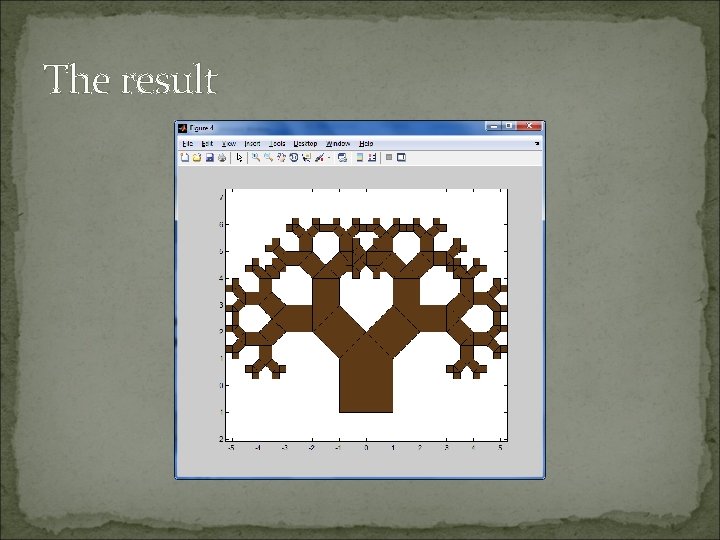
The result
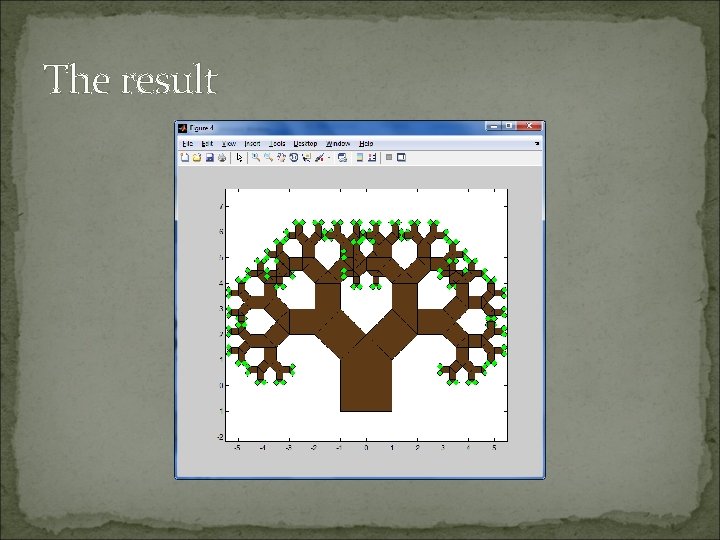
The result

Thank you for your attention!
- Slides: 20