Recursive Definition of Tree Structures 1 Empty is

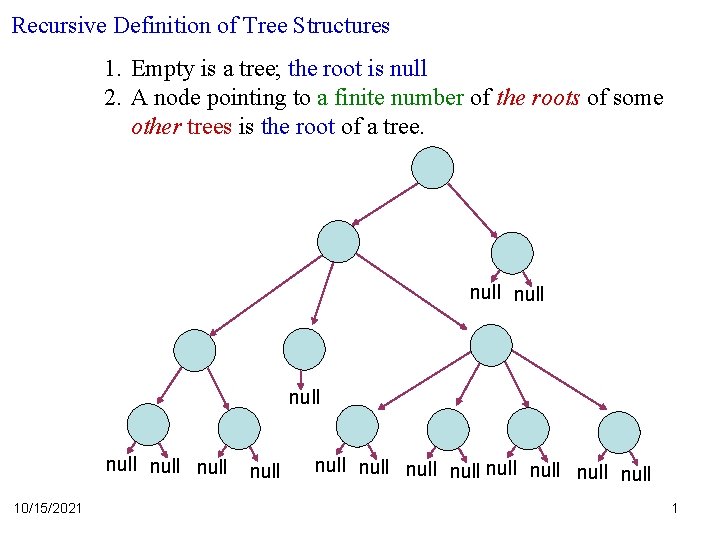
Recursive Definition of Tree Structures 1. Empty is a tree; the root is null 2. A node pointing to a finite number of the roots of some other trees is the root of a tree. null null 10/15/2021 null null null 1

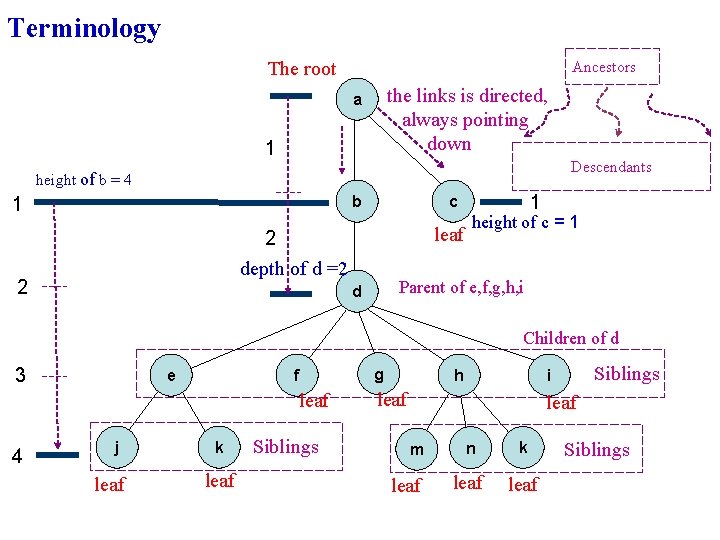
Terminology The root Ancestors the links is directed, always pointing down a 1 Descendants height of b = 4 b 1 leaf 2 depth of d =2 2 1 c height of c = 1 Parent of e, f, g, h, i d Children of d 3 e f leaf 4 j leaf k leaf Siblings g h Siblings i leaf m leaf n k leaf Siblings

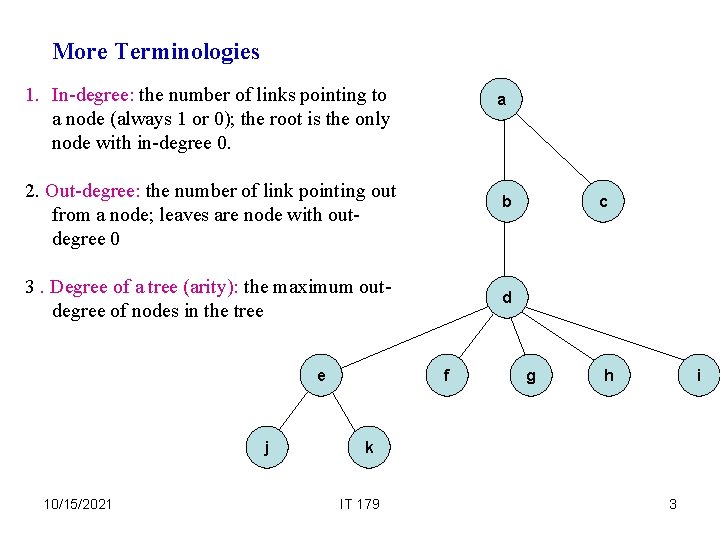
More Terminologies 1. In-degree: the number of links pointing to a node (always 1 or 0); the root is the only node with in-degree 0. a 2. Out-degree: the number of link pointing out from a node; leaves are node with outdegree 0 b 3. Degree of a tree (arity): the maximum outdegree of nodes in the tree e j 10/15/2021 c d f g h i k IT 179 3

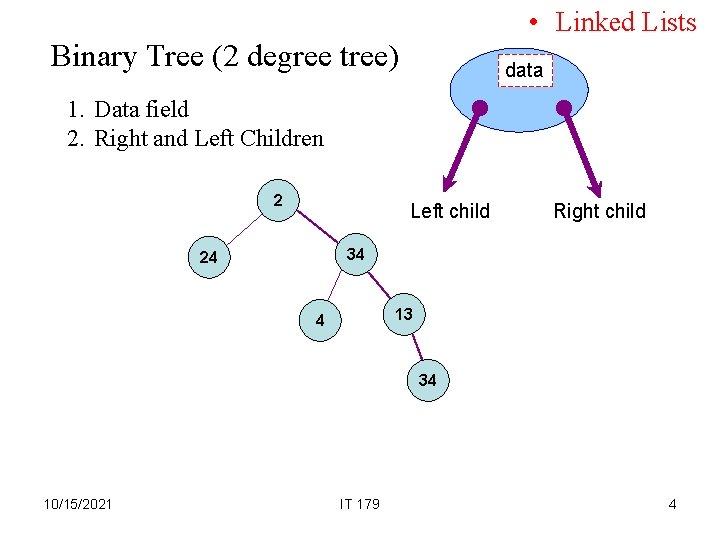
• Linked Lists Binary Tree (2 degree tree) data 1. Data field 2. Right and Left Children 2 Left child Right child 34 24 13 4 34 10/15/2021 IT 179 4

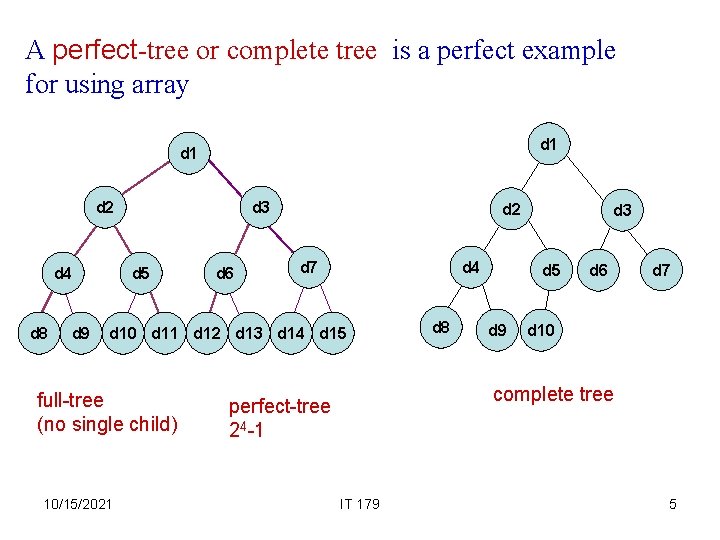
A perfect-tree or complete tree is a perfect example for using array d 1 d 2 d 4 d 8 d 9 d 3 d 5 d 6 d 2 d 7 d 4 d 10 d 11 d 12 d 13 d 14 d 15 full-tree (no single child) 10/15/2021 d 8 d 3 d 5 d 9 d 6 d 7 d 10 complete tree perfect-tree 24 -1 IT 179 5

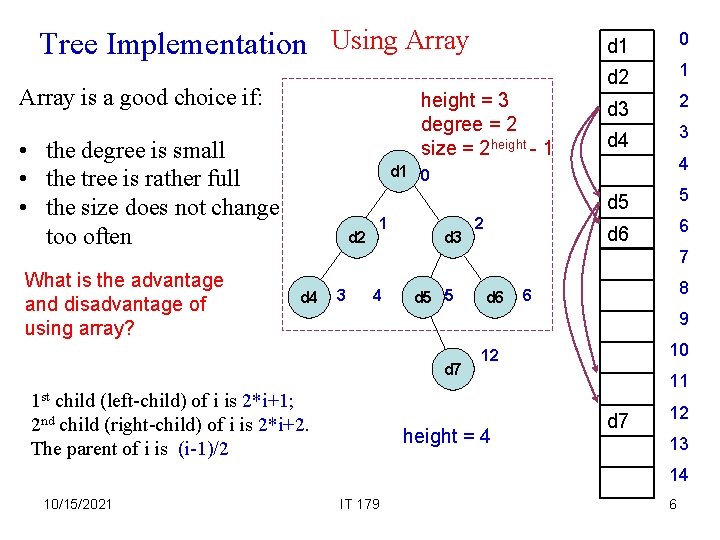
Tree Implementation Using Array is a good choice if: height = 3 degree = 2 size = 2 height - 1 • the degree is small • the tree is rather full • the size does not change too often What is the advantage and disadvantage of using array? d 1 0 d 2 1 d 3 2 d 4 3 4 d 1 0 d 2 1 d 3 2 d 5 5 d 6 6 7 d 4 3 4 d 5 5 d 6 8 6 9 d 7 1 st child (left-child) of i is 2*i+1; 2 nd child (right-child) of i is 2*i+2. The parent of i is (i-1)/2 10 12 height = 4 11 d 7 12 13 14 10/15/2021 IT 179 6

Tree Implementation: linked lists arrays • Links data 1. data field 2. enough fields for pointers pointing the children Usually, we use the degree of the tree as the number of the pointer fields. Fixed, if the degree is small, e. g. , binary tree (degree is 2). 10/15/2021 IT 179 7

1. 2. A Binary Tree Node in Java A data field Two pointers to the leftchild and right-child public class Binary. Tree <T> { /***** This is an inner class for tree nodes******/ private static class TNode<E> { private E data; private TNode<E> left, right; private TNode(E data, TNode<E> left, TNode<E> right) {//Construct a node with two children this. data = data; this. left = left; this. right = right; } } /***** This is the end of the inner class TNode<E> *******/ private TNode<T> root; public Binary. Tree() { root = null; }. . . 10/15/2021 IT 179 8

Calculate the size of the tree, i. e. , the number of nodes X nl + 1 + nr root = null; 0 nr nl // Return the number nodes in the tree. . . public int size() { return size(root); } private int size(TNode<E> t) { if (t == null) return 0; return 1 + size(t. left) + size(t. right); } 10/15/2021 IT 179 9

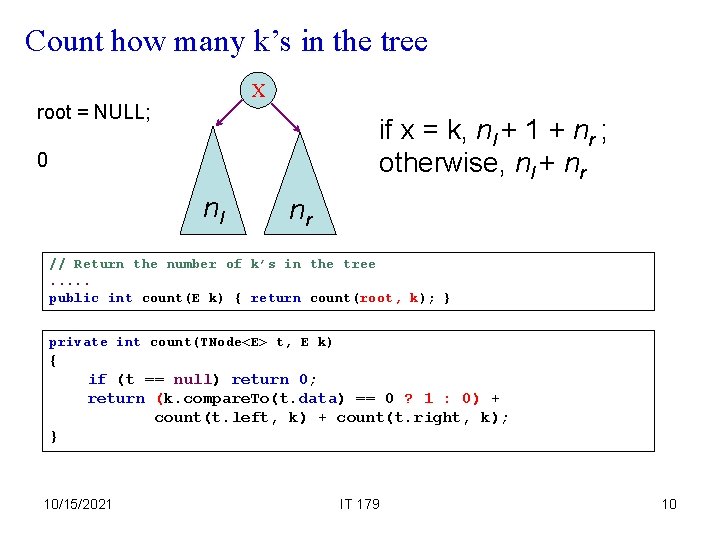
Count how many k’s in the tree X root = NULL; if x = k, nl + 1 + nr ; otherwise, nl + nr 0 nl nr // Return the number of k’s in the tree. . . public int count(E k) { return count(root, k); } private int count(TNode<E> t, E k) { if (t == null) return 0; return (k. compare. To(t. data) == 0 ? 1 : 0) + count(t. left, k) + count(t. right, k); } 10/15/2021 IT 179 10

Height of a Tree: The number of nodes in the longest path from the root. // Return the heights of the tree. . . public int height() { return height(root); } Private int height(TNode<T> t) { if (t == null) return 0; int L = height(t. left); int R = height(t. right); return 1 + (L > R ? L : R); } b a 1 c 2 3 d e g 10/15/2021 height = 5 root IT 179 4 f h 5 11

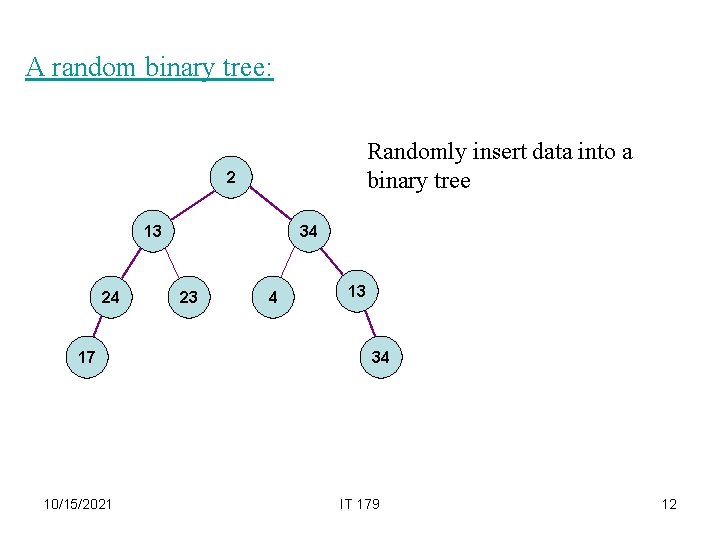
A random binary tree: Randomly insert data into a binary tree 2 13 24 17 10/15/2021 34 23 4 13 34 IT 179 12

Add a new data to the Binary. Tree //add data to this BST, return false if data is already in the tree public void add(E data) { root = add(root, data); } A private overloaded add method; 10/15/2021 IT 179 13

Randomly Insert (add) a data into a binary tree: data toss a coin head data private TNode<E> add(TNode<E> node, E data){ if (node == null) return new Node<E>(data, null); if (Math. random() < 0. 5) // toss a coin node. left = add(node. left, data); else node. right = add(node. right, data); return node; } 10/15/2021 IT 179 14

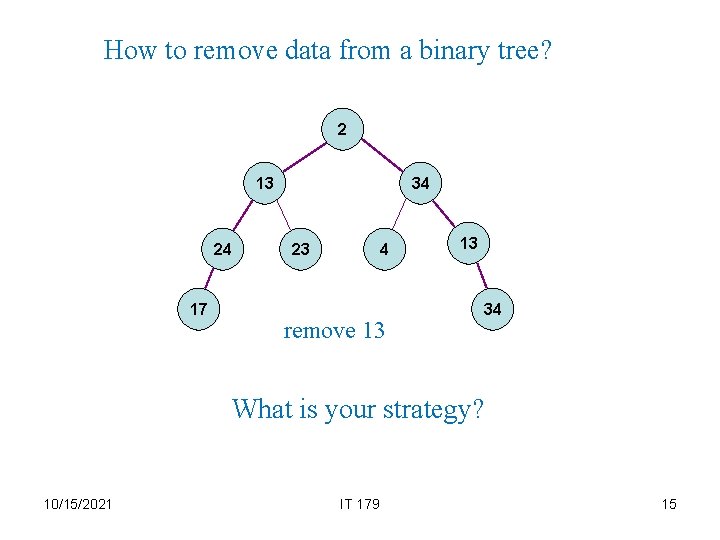
How to remove data from a binary tree? 2 13 24 17 34 23 4 remove 13 13 34 What is your strategy? 10/15/2021 IT 179 15

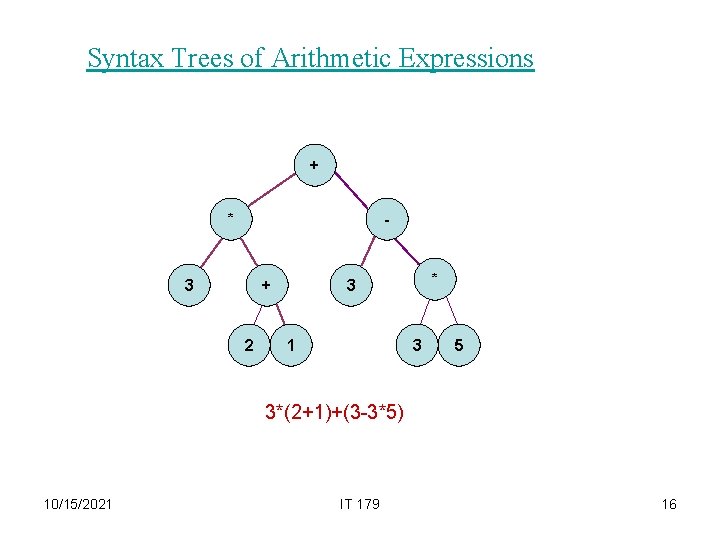
Syntax Trees of Arithmetic Expressions + * - 3 + 2 * 3 1 3 5 3*(2+1)+(3 -3*5) 10/15/2021 IT 179 16

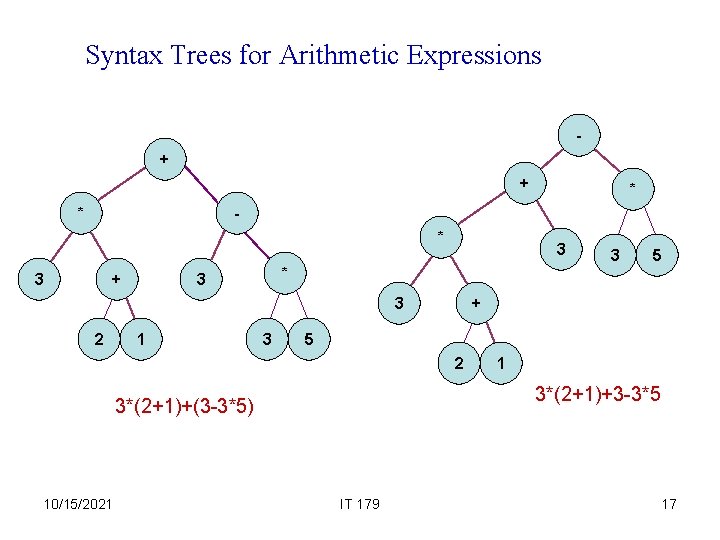
Syntax Trees for Arithmetic Expressions + + * * * 3 + 3 1 3 + 5 2 1 3*(2+1)+3 -3*5 3*(2+1)+(3 -3*5) 10/15/2021 5 * 3 3 2 3 IT 179 17

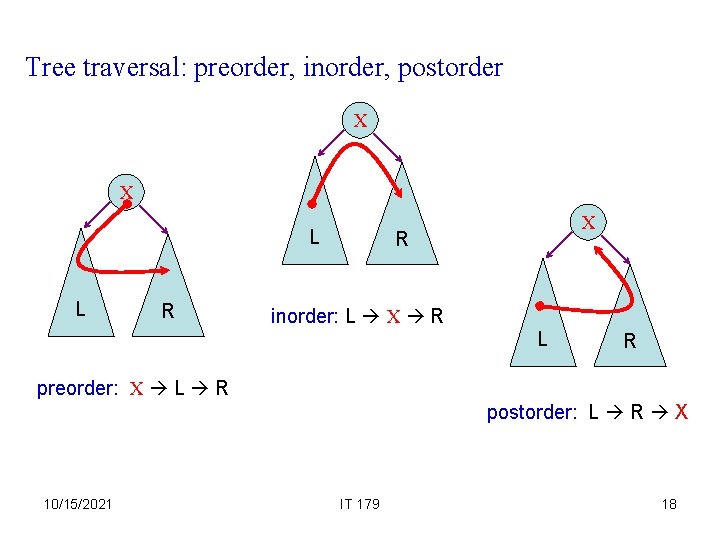
Tree traversal: preorder, inorder, postorder X X L L R X R inorder: L X R L R preorder: X L R postorder: L R X 10/15/2021 IT 179 18

// Three ways of traversals. . . public void inorder() { inorder(root); } public void preorder() { preorder(root); } public void postorder() { postorder(root); }. . . private void inorder(TNode<E> t) { if (t==null) return; inorder(t. left); System. out. print(t. data+", "); inorder(t. right); // (1) Travel to the left-child // (2) The way we visit the node // (3) Travel to the right-child } private void preorder(TNode<E> t) { if (t==null) return; System. out. print(t. data+", "); preorder(t. left); preorder(t. right); } private void postorder(TNode<E> t) { if (t==null) return; postorder(t. left); postorder(t. right); System. out. print(t. data+", "); } 10/15/2021 IT 179 // (1) The way we visit the node // (2) Travel to the left-child // (3) Travel to the right-child // (1) Travel to the left-child // (2) Travel to the right-child // (3) The way we visit the node 19