Recursion zyineleme Recursion zyineleme nedir Problemleri daha basit

Recursion (Özyineleme)

Recursion (Özyineleme) nedir? • Problemleri daha basit alt problemlere bölerek çözme yöntemi. • Alt problemler de kendi içlerinde başka alt problemlere bölünebilir. • Alt problemler çözülebilecek kadar küçülünce bölme işlemi durur. • Özyinelemeli bir algoritma bir problemi çözmek için problemi iki veya daha fazla alt probleme bölen bir yöntemdir.

Basamak Sayısı • Recursive definition digits(n) = 1 1 + digits(n/10) -> if (– 9 <= n <= 9) -> otherwise • Example digits(321) = 1 + digits(321/10) = 1 +digits(32) = 1 + [1 + digits(32/10)] = 1 + [1 + digits(3)] = 1 + [1 + (1)] = 3

Basamak Sayısı int basamak. Sayisi(int n) { if ((-10 < n) && (n < 10)) return 1 else return 1 + basamak. Sayisi (n/10); }

Özyineleme • f(x) problemini çözmek istiyorsak fakat direkt olarak çözemiyorsak • Varsayalım y`nin x`den küçük herhangi bir değeri için f(y)yi çözebiliyoruz • f(x)`i çözmek için f(y)`yi kullanırız • Bu yöntemin çalışabilmesi için f(x)`in direkt olarak hesaplanabildiği en az bir x değerinin olması gerekir. (e. g. base cases)

Bir Sayının kuvvetini hesaplama static int // k`nın if (n == return else return } power(int k, int n) { n. üssü 0) 1; k * power(k, n – 1);

Faktoriyel • 5! = 5*4*3*2*1 4! = 4*3*2*1 3! = 3*2*1 2! = 2*1 1! = 1 int faktoriyel = 1; for ( int sayac = 5; sayac>= 1; sayac-- ) faktoriyel = faktoriyel *sayac;

Özyinelemeli Faktöriyel public int faktoriyel(int N) { if (N == 0) return 1; return N*faktoriyel(N-1); }

Recursive Factorial

public double faktoriyel(int n, int sayac){ double fakt; if(n<=0){ System. out. println("Birinci Duruma ulasti"); fakt = 1; } else{ sayac++; System. out. println("Program cagiriyor " + sayac); fakt = n* faktoriyel 1(n-1, sayac); //System. out. println("Faktoriyel = " + fakt); } System. out. println("Programdan Cikiyor " + sayac); sayac --; return fakt; }

Faktoriyel programında ozyinelemeli metodların çağrılması Program cagiriyor 1 Program cagiriyor 2 Program cagiriyor 3 Program cagiriyor 4 Program cagiriyor 5 Birinci Duruma ulasti Programdan Cikiyor 5 Programdan Cikiyor 4 Programdan Cikiyor 3 Programdan Cikiyor 2 Programdan Cikiyor 1 5! = 120. 0

Fibonacci Sayıları

Fibonacci Java public int fibonacci(int sayi) { if ( ( sayi == 0 ) || ( sayi == 1 ) return sayi; else return fibonacci( sayi - 1 ) + fibonacci( sayi - 2 ); }

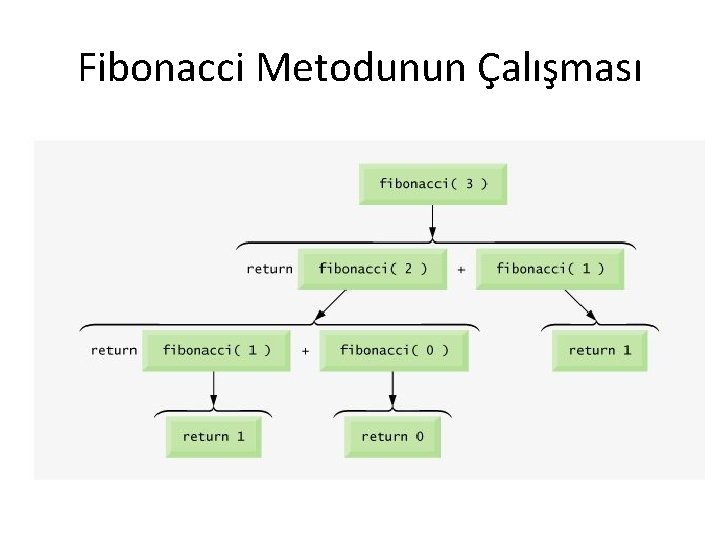
Fibonacci Metodunun Çalışması

Towers of Hanoi (Hanoi Kuleleri) • Legend has it that in a temple in the Far East, priests are attempting to move a stack of golden disks from one diamond peg to another. • The initial stack has 64 disks threaded onto one peg and arranged from bottom to top by decreasing size. • The priests are attempting to move the stack from one peg to another under the constraints that exactly one disk is moved at a time and at no time may a larger disk be placed above a smaller disk. • Three pegs are provided, one being used for temporarily holding disks. • Supposedly, the world will end when the priests complete their task, so there is little incentive for us to facilitate their

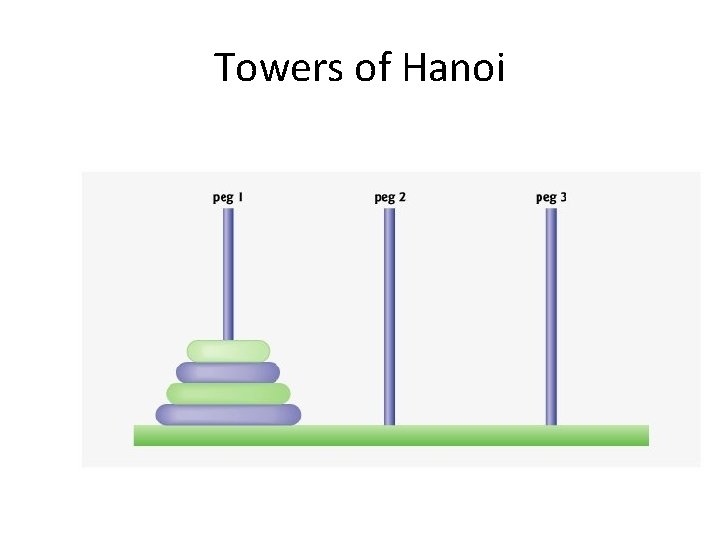
Towers of Hanoi

Towers of Hanoi Algoritması • Move n - 1 disks from peg 1 to peg 2, using peg 3 as a temporary holding area. • Move the last disk (the largest) from peg 1 to peg 3. • Move the n - 1 disks from peg 2 to peg 3, using peg 1 as a temporary holding area.

//Towers of Hanoi // recusively move disks through towers public void solve. Towers( int disks, int source. Peg, int destination. Peg, int temp. Peg ) { // base case -- only one disk to move if ( disks == 1 ) { System. out. println(source. Peg + " -> " +destination. Peg ); return; } // end if // recursion step -- move disk to temp. Peg, then to destination. Peg // move ( disks - 1 ) disks from source. Peg to temp. Peg recursively solve. Towers( disks - 1, source. Peg, temp. Peg, destination. Peg ); // move last disk from source. Peg to destination. Peg System. out. println(source. Peg + " -> " +destination. Peg ); // move ( disks - 1 ) disks from temp. Peg to destination. Peg solve. Towers( disks - 1, temp. Peg, destination. Peg, source. Peg ); } // end method solve. Towers

Towers Of Hanoi Çözüm • • 1 --> 3 1 --> 2 3 --> 2 1 --> 3 2 --> 1 2 --> 3 1 --> 3