Recursion What is Recursion n n Method of

Recursion

What is Recursion? n n Method of solving problems Alternative to iteration All recursive solutions can be implemented iteratively Characteristic. . . n n recursive methods call themselves recursive functions defined in terms of (simpler versions) themselves General recursive case & stopping cases

Factorial N n Iterative n n N! = N * N-1 * N-2 … 2 * 1 Recursive n n 1! = 1 N! = N * (N-1)! - stopping case - general case implement & trace in C++

Factorial Solution int fact( int n ) { if ( n == 0 || n == 1 ) { return 1; } else { return fact(n-1)*n; } // What are some problems here

Fibonacci Numbers n Find fib(n) given the definition : n n n fib(0) = 1 f ib(1) = 1 fib(n) = fib(n-1) + fib(n-2)

Solution public int fib( int n ) { if ( n == 0 || n == 1 ) { return 1; } else { return fib( n - 1 ) + fib( n - 2 ); } } naturally recursive, however better-off being solved iteratively. What are the problems here?

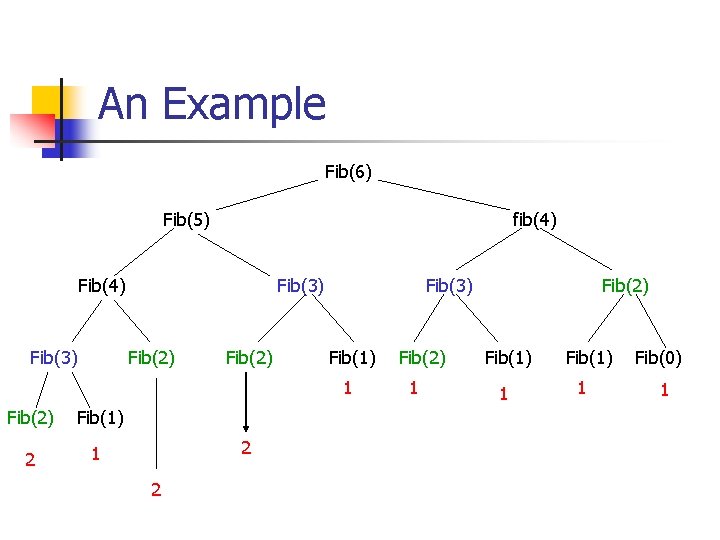
An Example Fib(6) Fib(5) fib(4) Fib(3) Fib(2) Fib(3) Fib(1) 1 Fib(2) Fib(1) 2 1 2 2 Fib(2) 1 Fib(2) Fib(1) 1 Fib(0) 1

Cache the results in the array static int fib(int n) { int[] sols = new int[n + 1]; sols[0] = 1; sols[1] = 1; return fib(n, sols) } static int fib(int n, int[] sols) { if (sols[n] > 0) return sols[n]; int sol = fib(n-1, sols) + fib(n-2, sols); sols[n] = sol; return sol; }

So, why use recursion? n Advantages. . . n n n Interesting conceptual framework Intuitive solutions to difficult problems But, disadvantages. . . n n requires more memory & time requires different way of thinking!

Towers of Hanoi n The Problem… n Rules n n n only move one disk at a time can’t put a disk on a smaller one Monks believed world would end once solved for 64 disks! Takes 580 billion years! at one move per sec.

An Approach n n To solve such problems ask yourself: "if I had solved the n-1 case could I solve the n case? " If the answer to this question is positive you proceed under the outrageous assumption that the n-1 case has been solved. Oddly enough this works, so long as there is some base case (often when n is zero or one) which can be treated as a special case.

N rings from pole A to pole C? n If you know how to move n-1 rings from one pole to another then simply move n -1 rings to the spare pole - there is only one ring left on the source pole now, simply move it to the destination, then pile the rest of them from the spare pole onto the destination pole.

Hanoi… n http: //www. mazeworks. com/hanoi/ void move. Tower (int num. Disks, int start, int end, int temp) { if (num. Disks == 1) move. One. Disk (start, end); else { move. Tower (num. Disks-1, start, temp, end); move. One. Disk (start, end); move. Tower (num. Disks-1, temp, end, start); } }

Print reverse n Print first N values in reverse Given. . . print. . . 5 7 2 6 3 n n 3, 6, 2, 7, 5 Simple iterative solution… Recursive? n n Hint - what is the simplest case? Write out sequence of cases & look for previous case within each case generalise & note stopping case!

Print reverse - solution n Solution form 5 7 2 6 3 N-1 N’th Write C++ & trace To print N values in reverse order if N > 0 Print the N’th value & then Print the preceding N-1 values in reverse order

Print forward n n Print set of values in normal order Solution form 5 7 2 6 3 N-1 Write C++ & trace N’th To print N values in normal order if N > 0 Print the first N-1 values in normal order & then Print the N’th value

Print – alternative solution n n Print set of values in order Alternative solution 5 7 2 6 3 first S rest E Write C++& trace To print values btw S & E in order if S <= E Print the value at S & then Print the values btw S+1 & E in order

Find Max n Find max of first N values 5 7 2 6 3 N-1 N’th Think about solution in terms of these two subproblems To find max of N values if N = 1 return N’th value else return greater of N’th & max of preceding N-1 values

Sequential search 5 7 2 6 3 N-1 N’th Think about simplest cases of problem & more general solution in terms of these two sub-problems Search( first N values of X for target) if N = 0 return not found else if N’th value is target O(N) return found at N’th else return search( first N-1 values of X for target)

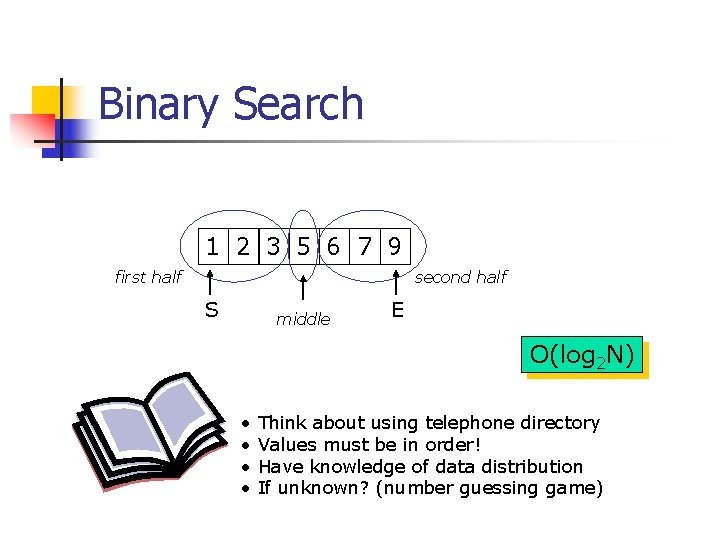
Binary Search 1 2 3 5 6 7 9 first half second half S middle E O(log 2 N) • • Think about using telephone directory Values must be in order! Have knowledge of data distribution If unknown? (number guessing game)

Binary Search (continued…) Search( X btw S & E for target) if S > E First half is S, middle-1 return not found Second half is else if ( middle value is target) middle+1, E return found at middle else if ( target < middle value) return search( first half of X for target) else return search( second half of X for target)

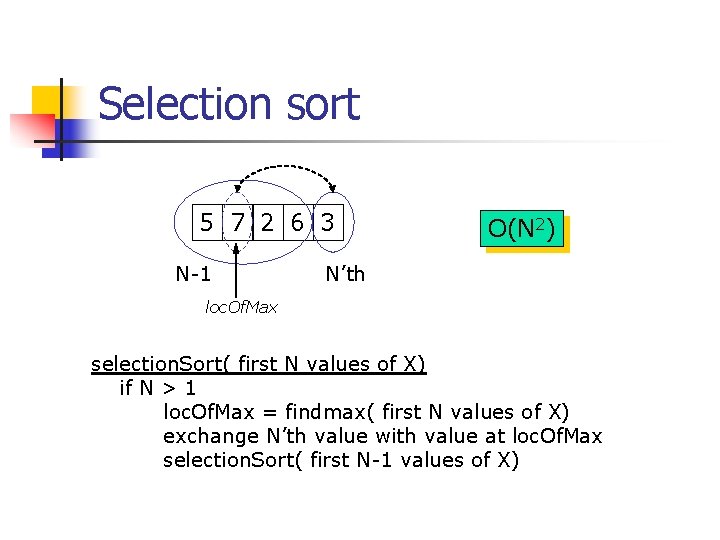
Selection sort 5 7 2 6 3 N-1 O(N 2) N’th loc. Of. Max selection. Sort( first N values of X) if N > 1 loc. Of. Max = findmax( first N values of X) exchange N’th value with value at loc. Of. Max selection. Sort( first N-1 values of X)

Quick. Sort O(Nlog 2 N) 5 7 3 9 2 1 6 pivot partition 2 1 3 5 7 9 6 Sort first part pivot Sort second part Quick. Sort( X btw S & E) if S < E pivot loc. = partition( X btw S & E) Quick. Sort( first part of X) Quick. Sort( second part of X) First part is S to pivot loc. -1 Second part is pivot loc. +1 to E

Merge. Sort O(Nlog 2 N) 1 5 7 9 2 3 6 Sort second half Sort first half merge 1 2 3 5 6 7 9 Merge. Sort( X btw S & E) if S < E Merge. Sort( first half of X) Merge. Sort( second half of X) Merge( first & second halves of X) Merge is the basis of sequential processing

Counting n Count number of values before zero 5 7 2 0 3 first S rest Zero is sentinel value & so is guaranteed to exist. This is a common form of representation for strings! count no. values before zero starting at S if value at S is zero return 0 else return 1 + count no. values starting at S+1

Common mistakes! (1) sum = 0; public void count( int[] X, int S) { if ( X[S] != 0) { sum++; count( X, S+1); } } Problems: • Need another method to get. Count() • What happens if called again?

Common mistakes! (2) public int count( int[] X, int S) { int sum; if ( X[S] == 0) return sum; else { sum++; return count( X, S+1); } } Problem: • New instance of local variable for each instantiation!

Palindrome R A D A R first middle last is. Palindrome( word) if first >= last return true else if first char of word != last char of word return false else return is. Palindrome( middle of word)

Blob Count n n n A Blob is the union of adjacent cells Cells are represented by a two dimensional array: boolean[][] is. Full; The problem is to count the size of a blob starting from coordinates x, & y.

Blob Count, the plan n n have a recursive method that adds 1 to the count if the given cell is occupied, and recursively adds the numbers of 8 neighbors we need to remember which cells we already counted, and can use boolean[][] counted for this purpose

Blob count, algorithm public int count(boolean[][] cells, int x, int y) { boolean[][] counted = new boolean[cells. length][cells[0]. length] return count_(cells, counted, x, y) }

Blob Algorithm private int count_(boolean[][] cells, boolean[][] counted, int x, int y) { if ( x < 0 || x >= cells. length) return 0; if (y < 0 || y >= cells[0]. length) return 0; if ( counted[x][y]) return 0; if (!is. Full[x][y]) return 0; counted[x][y] = true; return 1 + count_(cells, counted, x+1, y) + count_(cells, counted, x, y+1) + count_(cells, counted, x+1, y+1) + … }

The plan… n n n Print set of N values forward & backward Repeat using S & E find max value search for target - sequential binary search sort - selection, quick, merge palindrome Count using S only Maze & blob counting Fractals? Recursive-descent-parsing? …on to data structures (stacks, queues, lists, trees, …)