Recursion vs Iteration The original Lisp language was










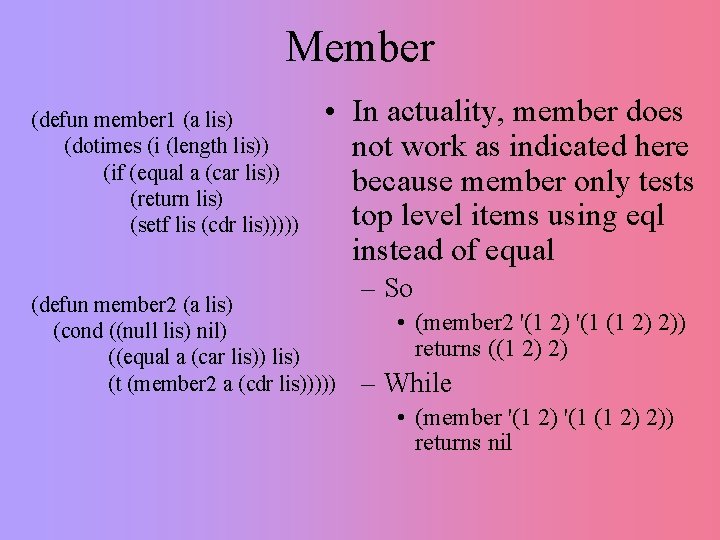










- Slides: 24

Recursion vs. Iteration • The original Lisp language was truly a functional language: – Everything was expressed as functions – No local variables – No iteration • You had to use recursion to get around these problems – Although they weren’t considered problems, functions are usually described recursively, and since the vision of Lisp was to model mathematical functions in a language, this was appropriate • But recursion is hard, in CL why should we use it? • Can’t we just use iteration?

Should we avoid recursive? • Recursion is hard: – It is hard to conceptualize how a problem can be solved recursively – Once implemented, it is often very difficult to debug a recursive program – When reading recursive code, it is sometimes hard to really see how it solves the problem • Recursion is inefficient: – Every time we recurse, we are doing another function call, this results in manipulating the run-time stack in memory, passing parameters, and transferring control • So recursion costs us both in time and memory usage – Consider the example on the next slide which compares iterative and recursive factorial solutions

A Simple Comparison (defun ifact (n) Here, the function is (let ((product 1)) called once, there are two (do ((j 0 (+ 1 j))) ((= j n)) local variables (setf product (* product (+ j 1)))) product)) The loop does a comparison and if the terminating condition is not yet true, we branch back up to the top (defun rfact (n) (if (< n 1) 1 (* n (rfact (- n 1))))) Total instructions: n * 5 + 3 Here, we have less code, no local variables (only a parameter) and fewer total instructions in the code, each iteration has a comparison and then either returns 1 or performs 3 function calls (-, rfact, * in that order) But we aren’t seeing the stack manipulations which require pushing a new n, space for the function’s return value, and updating the stack pointer register, and popping off the return value and n when done

Why Recursion? • If recursion is harder to understand less efficient, why use it? – It leads to elegant solutions – less code, less need for local variables, etc – If we can define a function mathematically, the solution is easy to codify – Some problems require recursion • • Tree traversals Graph traversals Search problems Some sorting algorithms (quicksort, mergesort) – Note: this is not strictly speaking true, we can accomplish a solution without recursion by using iteration and a stack, but in effect we would be simulating recursion, so why not use it? • In some cases, an algorithm with a recursive solution leads to a lesser computational complexity than an algorithm without recursion – Compare Insertion Sort to Merge Sort for example

Lisp is Set Up For Recursion • As stated earlier, the original intention of Lisp was to model mathematical functions so the language calls for using recursion – Basic form: (defun name (params) (if (terminating condition) return-base-case-value (name (manipulate params)))) – The components here are to test for a base case and if true, return the base cases’ value, otherwise recurse passing the function the parameter(s) manipulated for the next level

What Happens During Recursion • You should have studied this in 262, but as a refresher: – We use the run-time stack to coordinate recursion – The stack gives us a LIFO access • Imagine that function 1 calls function 2 which calls function 3 • When function 3 ends, where do we return to? Run-time stack: main calls m 1 calls m 2 calls m 3 calls m 4 We are currently in m 4 – the run-time stack stores the location in function 2 to return to Main • When function 2 ends, where do we return to? m 1 – the run-time stack stores the location in function 1 to return to – etc – Using a stack makes it easy to “backtrack” to the proper location when a method ends • Notice that we want this behavior whether we are doing normal function calls or recursion m 2 m 3 stack pointer m 4

More On the Run-time Stack • For each active function, the run-time stack stores an “activation record instance” – This is a description of the function’s execution and stores • Local variables, Parameters, Return value • Return pointer (where to return to in the calling function upon function termination) • Every time a function (or method in Java) is called – the run-time stack is manipulated by pushing a new activation record instance onto it – proper memory space is allocated on the stack for all local variables and parameters – the return pointer is set up – the stack pointer register is adjusted • Every time a function terminates – the run-time stack has the top activation record instance popped off of it, returning the value that the function returns – the PC (program counter register) is adjusted to the proper location in the calling function – the stack pointer register is adjusted

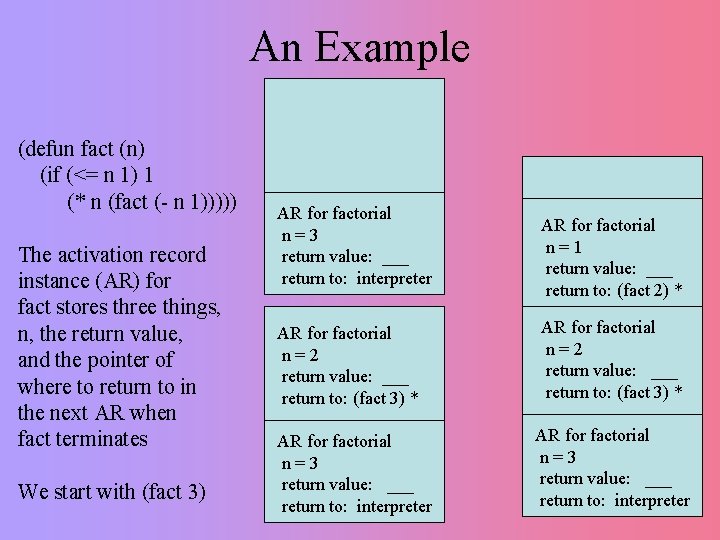
An Example (defun fact (n) (if (<= n 1) 1 (* n (fact (- n 1))))) The activation record instance (AR) for fact stores three things, n, the return value, and the pointer of where to return to in the next AR when fact terminates We start with (fact 3) AR for factorial n=3 return value: ___ return to: interpreter AR for factorial n=2 return value: ___ return to: (fact 3) * AR for factorial n=3 return value: ___ return to: interpreter AR for factorial n=1 return value: ___ return to: (fact 2) * AR for factorial n=2 return value: ___ return to: (fact 3) * AR for factorial n=3 return value: ___ return to: interpreter

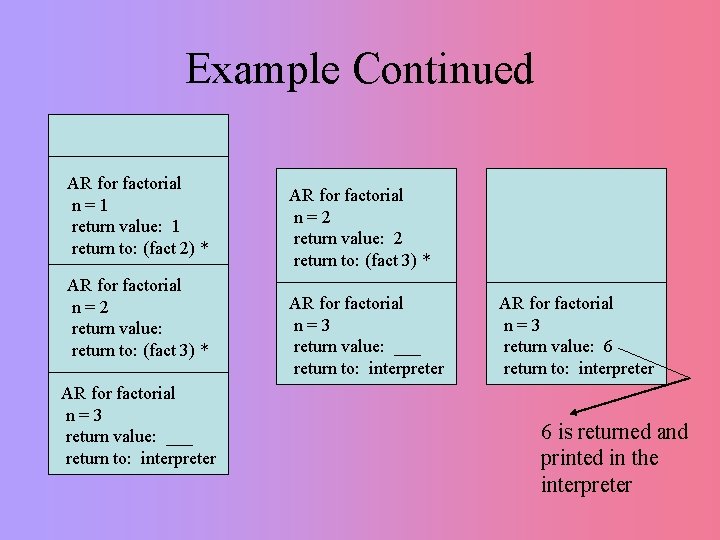
Example Continued AR for factorial n=1 return value: 1 return to: (fact 2) * AR for factorial n=2 return value: return to: (fact 3) * AR for factorial n=3 return value: ___ return to: interpreter AR for factorial n=2 return value: 2 return to: (fact 3) * AR for factorial n=3 return value: ___ return to: interpreter AR for factorial n=3 return value: 6 return to: interpreter 6 is returned and printed in the interpreter

Lisp Makes Recursion Easy • Well, strictly speaking, recursion in Lisp is similar to recursion in any language • What Lisp can do for us is give us easy access to the debugger – You can insert a (break) instruction which forces the evaluation step of the REPL cycle to stop executing, leaving us in the debugger – Or, if you have a run-time error, you are automatically placed into the debugger – From the debugger you can • inspect the run-time stack to see what values are there • return to a previous level of recursive call • provide a value to be returned – Thus, you can either determine • why you got an error by inspecting the stack • see what is going on in the program by inspecting the stack • return from an error by inserting a partial or complete solution • CL can also make a recursive program more efficient (to be explained later)

Examples of Recursive Code • Every List function in CL can be implemented recursively – whether they are or not I’m not sure, but probably they are • Here we start with 3 versions of last (defun last (lis) (cond ((null (cdr lis)) (car lis)) (t (last (cdr lis))))) (defun last 2 (lis) (cond ((and (listp lis) (= (length lis) 1)) lis) (t (last 2 (cdr lis))))) (defun last 3 (lis) (cond ((atom lis) (list lis)) ((and (listp lis) (= (length lis) 1)) lis) (t (last 3 (cdr lis))))) The top definition returns an atom, the bottom definition can handle atoms and Lists, CL’s last is probably last 2

Butlast With and Without Recursion (defun butlast 1 (lis) (cdr (reverse (cdr lis)))) (defun mybutlast (lis) (cond ((null (cdr lis)) nil) (t (cons (car lis) (mybutlast (cdr lis)))))) The iterative version of reverse builds a list iteratively using a local variable (defun reverse 1 (lis) (let (temp (size (length lis))) (dotimes (a size) (setf temp (append temp The recursive (list (nth (- (- size a) 1) lis))))) version, while temp) being harder to understand, (defun reverse 2 (lis) contains far (if (null lis) nil less code (append (reverse 2 (cdr lis)) (list (car lis)))))
Member (defun member 1 (a lis) (dotimes (i (length lis)) (if (equal a (car lis)) (return lis) (setf lis (cdr lis))))) • In actuality, member does not work as indicated here because member only tests top level items using eql instead of equal (defun member 2 (a lis) (cond ((null lis) nil) ((equal a (car lis)) lis) (t (member 2 a (cdr lis))))) – So • (member 2 '(1 2) '(1 (1 2) 2)) returns ((1 2) 2) – While • (member '(1 2) '(1 (1 2) 2)) returns nil

Nth and Nthcdr (defun nth (n lis) (dotimes (a n) (setf lis (cdr lis))) (car lis)) (defun nth 2 (a lis) (cond ((= a 0) (car lis)) (t (nth 2 (- a 1) (cdr lis))))) (defun nth 3 (a lis) (cond ((< a 0) nil) ((= a 0) (car lis)) (t (nth 3 (- a 1) (cdr lis))))) (defun nthcdr 1 (n lis) (dotimes (a n) (setf lis (cdr lis))) lis) (defun nthcdr 2 (n lis) (cond ((< n 0) nil) ((= n 0) lis) (t (nthcdr 2 (- n 1) (cdr lis)))))

Remove from a List (defun remove 1 (a lis) (let ((temp nil)) (dolist (i lis) (if (not (equal a i)) (setf temp (append temp (list i))))) temp)) (defun remove 2 (a lis) (cond ((null lis) nil) ((equal a (car lis)) (remove 2 a (cdr lis))) (t (cons (car lis) (remove 2 a (cdr lis)))))) (defun remove-first (a lis) (cond ((null lis) nil) ((equal a (car lis)) (cdr lis)) (t (cons (car lis) (remove-first a (cdr lis)))))) What would remove-last look like?

Substitute Item In List (defun subs 1 (a b lis) (let ((temp nil)) (dolist (i lis) (if (equal a i) (setf temp (append temp (list b))) (setf temp (append temp (list i))))) temp)) (defun subs 2 (a b lis) (cond ((null lis) nil) ((equal a (car lis)) (cons b (subs 2 a b (cdr lis)))) (t (cons (car lis) (subs 2 a b (cdr lis)))))) (defun sub-first (a b lis) (cond ((null lis) nil) ((equal a (car lis)) (cons b (cdr lis))) (t (cons (car lis) (sub-first a b (cdr lis))))))

Flattening a List • Now consider the problem of delistifying a list – That is, taking all of the items in sublists and moving them into the top-level list – The recursive version is fairly straightforward • If the parameter is nil, return the empty list • If the parameter is an atom, return the atom as a list • Otherwise, append what we get back by recursively calling this function with the car of the parameter (null, an atom, or a list) and the cdr of the parameter (null or a list) – Since sublists may contain subsublists, etc, an iterative version would be extremely complicated! (defun flatten (lis) (cond ((null lis) nil) (flatten ’(a (b c (d e) f (g)) ((h) i))) ((atom lis) (list lis)) (A B C D E F G H I) (t (append (flatten (car lis)) (flatten (cdr lis))))))

Counting List Items • We can count the top level items using length – (length ’(1 2 3 4)) 4 but (length ’(1 (2 3) 4)) 3 • We can implement a counting function easily enough as: (defun countitems (lis) (if (null lis) 0 (+ 1 (countitems (cdr lis))))) • Counting the total number of atoms in a list that might contain sublists requires flattening, so we instead would do this: (defun countallitems (lis) (cond ((null lis) 0) ((atom (car lis)) (+ 1 (countallitems (cdr lis)))) (t (+ (countallitems (car lis)) (countallitems (cdr lis))))))

Remove All • We might similarly want to remove all of an atom from the lists and sublists of a given list so again we turn to flattening: (defun removeall (a lis) (cond ((null lis) nil) ((equal a (car lis)) (removeall a (cdr lis))) ((listp (car lis)) (cons (removeall a (car lis)) (removeall a (cdr lis)))) (t (cons (car lis) (removeall a (cdr lis)))))) (removeall 'a '(a b (a c) (d ((a) b) a) c a)) returns (B (C) (D (NIL B)) C) Notice the nil inserted into the list because we replace (a) with nil, can we fix this? If so, how?

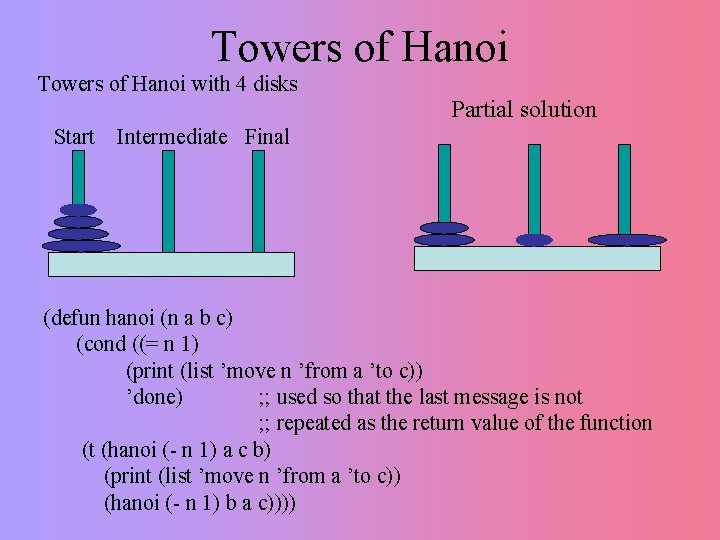
Towers of Hanoi with 4 disks Start Partial solution Intermediate Final (defun hanoi (n a b c) (cond ((= n 1) (print (list ’move n ’from a ’to c)) ’done) ; ; used so that the last message is not ; ; repeated as the return value of the function (t (hanoi (- n 1) a c b) (print (list ’move n ’from a ’to c)) (hanoi (- n 1) b a c))))

Tail Recursion • When writing recursive code, we typically write the recursive function call in a cond statement as: – (t (name (manipulate params))) • If the last thing that this function does is call itself, then this is known as tail recursion – Tail recursion is important because it can be implemented more efficiently – Consider the following implementation of factorial, why isn’t it tail recursive? (defun fact (n) (cond ((<= n 1) 1) (t (* n (fact (- n 1)))))) The last thing fact does is *, not fact so this is not tail recursive!

Writing Factorial with Tail Recursion • If you look carefully, you can see that * is done after we return from calling fact • This seems like a necessity because we define factorial as f(n) = n * f(n – 1) – So we must subtract 1, then call f, and then do multiplication – Can we somehow rearrange the code so that * is not performed last? Yes, by also passing a partial product as follows (defun fact-with-tr (n prod) (cond ((<= n 1) prod) (t (fact-with-tr (- n 1) (* n prod))))) We call this function as (fact-with-tr n 1) The last thing this function does is call fact-with-tr, not – or *

Why Bother With TR? • Optimizing compilers available in Common Lisp can benefit from tail recursion if they detect it – Rather than placing multiple Activation Record Instances on the stack, a single activation record instance is pushed onto the stack when the function is called the first time – For each recursive call, the same activation record instance is manipulated • in this case, n would be decremented and prod would be updated – Since we are guaranteed in any single recursive call that we will never need to use the parameter again in this call, we can change it • why are we guaranteed that a parameter’s value won’t change in this call? – And the return location is always to the same location in this function – Once the function terminates, it is popped off the stack and we return to the calling function’s location, or the interpreter – Note: we have a significant problem if an error arises and we are dropped into the debugger – what is that problem? • Aside from saving on memory usage and a bit of run-time memory allocation, this optimization doesn’t do anything else for us, so we don’t really have to worry about tail recursion

Search Problems • Lisp was the primary language for AI research – Many AI problems revolve around searching for an answer • Consider chess – you have to make a move, what move do you make? • A computer program must search from all the possibilities to decide what move to make – but you don’t want to search by just looking 1 move ahead – if you look 2 moves ahead, you don’t have twice as many possible moves, but the number of possible moves 2 – if you look 3 moves ahead, number of possible moves 3 – this can quickly get out of hand • So we limit our search by evaluating a top-level move using a heuristic function • If the function says “don’t make this move”, we don’t consider it and don’t search any further along that path • If the function says “possibly a good move”, then we recursively search – by using recursion, we can “backup” and try another route if needed, this is known as backtracking