Recursion Unrolling for Divide and Conquer Programs Radu























































- Slides: 75

Recursion Unrolling for Divide and Conquer Programs Radu Rugina and Martin Rinard Laboratory for Computer Science Massachusetts Institute of Technology

What This Talk Is About • Automatic generation of efficient large base cases for divide and conquer programs

Outline 1. Motivating Example 2. Computation Structure 3. Transformations 4. Related Work 5. Conclusion

1. Motivating Example

Divide and Conquer Matrix Multiply A A 0 A 1 A 2 A 3 B = B 0 B 1 B 2 B 3 = R A 0 B 0+A 1 B 2 A 0 B 1+A 1 B 3 A 2 B 0+A 3 B 2 A 2 B 1+A 3 B 3 • Divide matrices into sub-matrices: A 0 , A 1, A 2 etc • Use blocked matrix multiply equations

Divide and Conquer Matrix Multiply A A 0 A 1 A 2 A 3 B = B 0 B 1 B 2 B 3 = R A 0 B 0+A 1 B 2 A 0 B 1+A 1 B 3 A 2 B 0+A 3 B 2 A 2 B 1+A 3 B 3 • Recursively multiply sub-matrices

Divide and Conquer Matrix Multiply A B = R a 0 b 0 = a 0 b 0 • Terminate recursion with a simple base case

Divide and Conquer Matrix Multiply void matmul(int *A, int *B, int *R, int n) { Implements if (n == 1) { (*R) += (*A) * (*B); } else { matmul(A, B, R, n/4); matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); matmul(A+(n/4), B+2*(n/4), R, n/4); matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); } R += A B

Divide and Conquer Matrix Multiply void matmul(int *A, int *B, int *R, int n) { if (n == 1) { (*R) += (*A) * (*B); } else { matmul(A, B, R, n/4); matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); matmul(A+(n/4), B+2*(n/4), R, n/4); matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); } Divide matrices in sub-matrices and recursively multiply sub-matrices

Divide and Conquer Matrix Multiply Identify sub-matrices void matmul(int *A, int *B, int *R, int n) { if (n == 1) { with pointers (*R) += (*A) * (*B); } else { matmul(A, B, R, n/4); matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); matmul(A+(n/4), B+2*(n/4), R, n/4); matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); }

Divide and Conquer Matrix Multiply void matmul(int *A, int *B, int *R, int n) { if (n == 1) { (*R) += (*A) * (*B); } else { matmul(A, B, R, n/4); matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); matmul(A+(n/4), B+2*(n/4), R, n/4); matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); } Use a simple algorithm for the base case

Divide and Conquer Matrix Multiply void matmul(int *A, int *B, int *R, int n) { if (n == 1) { (*R) += (*A) * (*B); } else { matmul(A, B, R, n/4); matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); matmul(A+(n/4), B+2*(n/4), R, n/4); matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); } • Advantage of small base case: simplicity • Code is easy to: • • Write Maintain Debug Understand

Divide and Conquer Matrix Multiply • Disadvantage: void matmul(int *A, int *B, int *R, int n) { if (n == 1) { inefficiency (*R) += (*A) * (*B); } else { • Large control flow matmul(A, B, R, n/4); overhead: matmul(A, B+(n/4), R+(n/4), n/4); matmul(A+2*(n/4), B, R+2*(n/4), n/4); • Most of the time is matmul(A+2*(n/4), B+(n/4), R+3*(n/4), n/4); spent in dividing the matmul(A+(n/4), B+2*(n/4), R, n/4); matrix in sub-matrices matmul(A+(n/4), B+3*(n/4), R+(n/4), n/4); matmul(A+3*(n/4), B+2*(n/4), R+2*(n/4), n/4); matmul(A+3*(n/4), B+3*(n/4), R+3*(n/4), n/4); }

Hand Coded Implementation void serialmul(block *As, block *Bs, block *Rs) { int i, j; DOUBLE *A = (DOUBLE *) As; DOUBLE *B = (DOUBLE *) Bs; DOUBLE *R = (DOUBLE *) Rs; for (j = 0; j < 16; j += 2) { DOUBLE *bp = &B[j]; for (i = 0; i < 16; i += 2) { DOUBLE *ap = &A[i * 16]; DOUBLE *rp = &R[j + i * 16]; register DOUBLE s 0_0 = rp[0], s 0_1 = rp[1]; register DOUBLE s 1_0 = rp[16], s 1_1 = rp[17]; s 0_0 += ap[0] * bp[0]; s 0_1 += ap[0] * bp[1]; s 1_0 += ap[16] * bp[0]; s 1_1 += ap[16] * bp[1]; s 0_0 += ap[1] * bp[16]; s 0_1 += ap[1] * bp[17]; s 1_0 += ap[17] * bp[16]; s 1_1 += ap[17] * bp[17]; s 0_0 += ap[2] * bp[32]; s 0_1 += ap[2] * bp[33]; s 1_0 += ap[18] * bp[32]; s 1_1 += ap[18] * bp[33]; s 0_0 += ap[3] * bp[48]; s 0_1 += ap[3] * bp[49]; s 1_0 += ap[19] * bp[48]; s 1_1 += ap[19] * bp[49]; s 0_0 += ap[4] * bp[64]; s 0_1 += ap[4] * bp[65]; s 1_0 += ap[20] * bp[64]; s 1_1 += ap[20] * bp[65]; s 0_0 s 0_1 s 1_0 s 1_1 s 0_0 s 0_1 s 1_0 s 1_1 s 0_0 s 0_1 s 1_0 += += += += += += += += += ap[5] * bp[80]; ap[5] * bp[81]; ap[21] * bp[80]; ap[21] * bp[81]; ap[6] * bp[96]; ap[6] * bp[97]; ap[22] * bp[96]; ap[22] * bp[97]; ap[7] * bp[112]; ap[7] * bp[113]; ap[23] * bp[112]; ap[23] * bp[113]; ap[8] * bp[128]; ap[8] * bp[129]; ap[24] * bp[128]; ap[24] * bp[129]; ap[9] * bp[144]; ap[9] * bp[145]; ap[25] * bp[144]; ap[25] * bp[145]; ap[10] * bp[160]; ap[10] * bp[161]; ap[26] * bp[160]; ap[26] * bp[161]; ap[11] * bp[176]; ap[11] * bp[177]; ap[27] * bp[176]; ap[27] * bp[177]; ap[12] * bp[192]; ap[12] * bp[193]; ap[28] * bp[192]; ap[28] * bp[193]; ap[13] * bp[208]; ap[13] * bp[209]; ap[29] * bp[208]; s 1_1 += ap[29] s 0_0 += ap[14] s 0_1 += ap[14] s 1_0 += ap[30] s 1_1 += ap[30] s 0_0 += ap[15] s 0_1 += ap[15] s 1_0 += ap[31] s 1_1 += ap[31] rp[0] = s 0_0; rp[1] = s 0_1; rp[16] = s 1_0; rp[17] = s 1_1; * * * * * bp[209]; bp[224]; bp[225]; bp[240]; bp[241]; } } } cilk void matrixmul(long nb, block *A, block *B, block *R) { if (nb == 1) { flops = serialmul(A, B, R); } else if (nb >= 4) { spawn matrixmul(nb/4, A, B, R); spawn matrixmul(nb/4, A, B+(nb/4), R+(nb/4)); spawn matrixmul(nb/4, A+2*(nb/4), B+(nb/4), R+2*(nb/4)); spawn matrixmul(nb/4, A+2*(nb/4), B, R+3*(nb/4)); sync; spawn matrixmul(nb/4, A+(nb/4), B+2*(nb/4), R); spawn matrixmul(nb/4, A+(nb/4), B+3*(nb/4), R+(nb/4)); spawn matrixmul(nb/4, A+3*(nb/4), B+3*(nb/4), R+2*(nb/4)); spawn matrixmul(nb/4, A+3*(nb/4), B+3*(nb/4), R+3*(nb/4)); sync; } }

Goal • The programmer writes simple code with small base cases • The compiler automatically generates efficient code with large base cases

2. Computation Structure

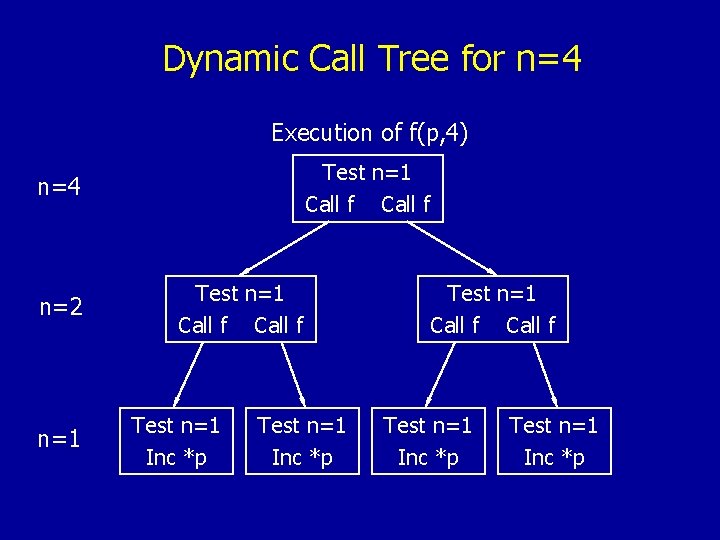
Running Example – Array Increment void f(char *p, int n) if (n == 1) { /* base case: increment one element */ (*p) += 1; } else { f(p, n/2); /* increment first half */ f(p+n/2, n/2); /* increment second half */ } }

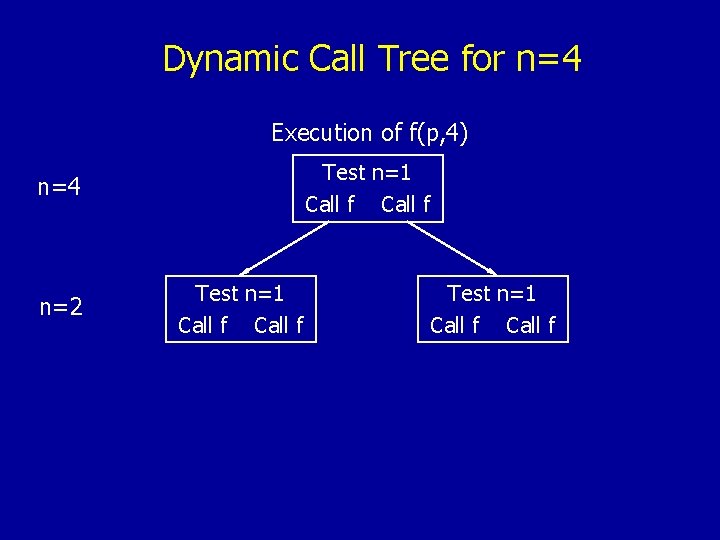
Dynamic Call Tree for n=4 Execution of f(p, 4)

Dynamic Call Tree for n=4 Execution of f(p, 4) Test n=1 Call f

Dynamic Call Tree for n=4 Execution of f(p, 4) Activation Frame on the Stack Test n=1 Call f

Dynamic Call Tree for n=4 Execution of f(p, 4) Test n=1 Call f Executed Instructions

Dynamic Call Tree for n=4 Execution of f(p, 4) Test n=1 Call f

Dynamic Call Tree for n=4 Execution of f(p, 4) Test n=1 Call f n=4 n=2 Test n=1 Call f

Dynamic Call Tree for n=4 Execution of f(p, 4) Test n=1 Call f n=4 n=2 n=1 Test n=1 Call f Test n=1 Inc *p

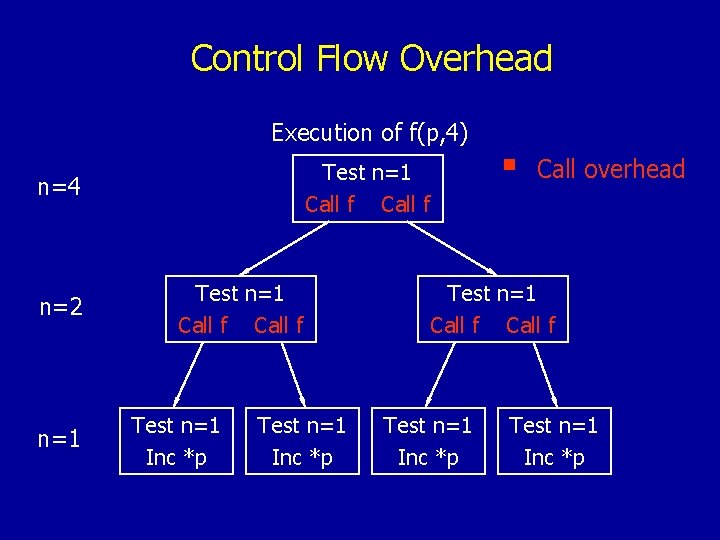
Control Flow Overhead Execution of f(p, 4) Test n=1 Call f n=4 n=2 n=1 Test n=1 Call f Test n=1 Inc *p § Call overhead Test n=1 Call f Test n=1 Inc *p

Control Flow Overhead Execution of f(p, 4) Test n=1 Call f n=4 n=2 n=1 Test n=1 Call f Test n=1 Inc *p § Call overhead + Test overhead Test n=1 Call f Test n=1 Inc *p

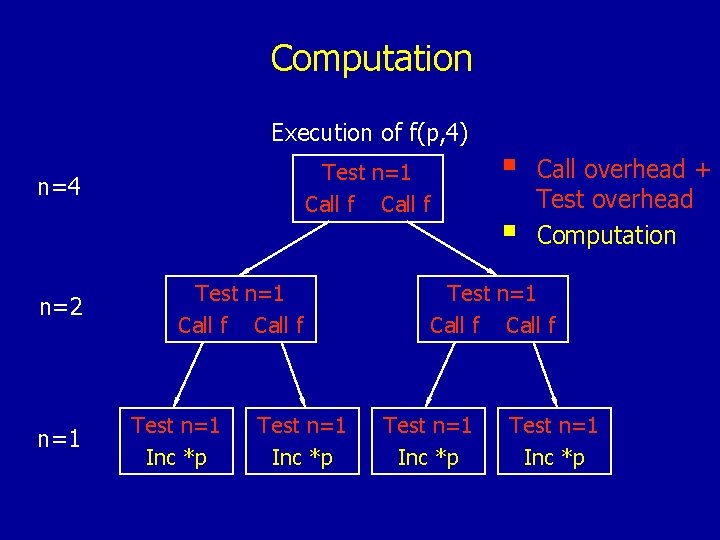
Computation Execution of f(p, 4) Test n=1 Call f n=4 n=2 n=1 Test n=1 Call f Test n=1 Inc *p § § Call overhead + Test overhead Computation Test n=1 Call f Test n=1 Inc *p

Large Base Cases = Reduced Overhead Execution of f(p, 4) Test n=2 Call f n=4 n=2 Test n=2 Inc *p Inc *(p+1)

3. Transformations

Transformation 1: Recursion Inlining Start with the original recursive procedure void f (char *p, int n) if (n == 1) { (*p) += 1; } else { f(p, n/2); f(p+n/2, n/2); }

Transformation 1: Recursion Inlining Make two copies of the original procedure void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); } void f 2(char *p, int n) if (n == 1) { (*p) += 1; } else { f 2(p, n/2); f 2(p+n/2, n/2); }

Transformation 1: Recursion Inlining Transform direct recursion to mutual recursion void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { f 2(p, n/2); f 2(p+n/2, n/2); } void f 2(char *p, int n) if (n == 1) { (*p) += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); }

Transformation 1: Recursion Inlining Inline procedure f 2 at call sites in f 1 void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { f 2(p, n/2); f 2(p+n/2, n/2); } void f 2(char *p, int n) if (n == 1) { (*p) += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); }

Transformation 1: Recursion Inlining void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { if (n/2 == 1) { *p += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); } if (n/2 == 1) { *(p+n/2) += 1; } else { f 1(p+n/2, n/2/2); f 1(p+n/2+n/4, n/2/2); } }

Transformation 1: Recursion Inlining void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { if (n/2 == 1) { *p += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); } if (n/2 == 1) { *(p+n/2) += 1; } else { f 1(p+n/2, n/2/2); f 1(p+n/2+n/4, n/2/2); } } • Reduced procedure call overhead • More code exposed at the intra-procedural level • Opportunities to simplify control flow in the inlined code

Transformation 1: Recursion Inlining void f 1(char *p, int n) if (n == 1) { (*p) += 1; } else { if (n/2 == 1) { *p += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); } if (n/2 == 1) { *(p+n/2) += 1; } else { f 1(p+n/2, n/2/2); f 1(p+n/2+n/4, n/2/2); } } • Reduced procedure call overhead • More code exposed at the intra-procedural level • Opportunities to simplify control flow in the inlined code: • identical condition expressions

Transformation 2: Conditional Fusion Merge if statements with identical conditions void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); f 1(p+n/2+n/4, n/2/2); }

Transformation 2: Conditional Fusion Merge if statements with identical conditions void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); f 1(p+n/2+n/4, n/2/2); } • Reduced branching overhead and bigger basic blocks • Larger base case for n/2 = 1

Unrolling Iterations Repeatedly apply inlining and conditional fusion void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); f 1(p+n/2+n/4, n/2/2); }

Second Unrolling Iteration void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else { f 1(p, n/2/2); f 1(p+n/2/2, n/2/2); f 1(p+n/2+n/4, n/2/2); } void f 2(char *p, int n) if (n == 1) { *p += 1; } else { f 2(p, n/2); f 2(p+n/2, n/2); }

Second Unrolling Iteration void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else { f 2(p, n/2/2); f 2(p+n/2/2, n/2/2); f 2(p+n/2+n/4, n/2/2); } void f 2(char *p, int n) if (n == 1) { *p += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); }

Result of Second Unrolling Iteration void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else if (n/2/2 == 1) { *p += 1; *(p+n/2/2) += 1; *(p+n/2+n/2/2) += 1; } else { f 1(p, n/2/2/2); f 1(p+n/2/2/2, n/2/2/2); f 1(p+n/2/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2+n/2/2/2, n/2/2/2); }

Unrolling Iterations • The unrolling process stops when the number of iterations reaches the desired unrolling factor • The unrolled recursive procedure: • Has base cases for larger problem sizes • Divides the given problem into more sub-problems of smaller sizes • In our example: • Base cases for n=1, n=2, and n=4 • Problems are divided into 8 problems of 1/8 size

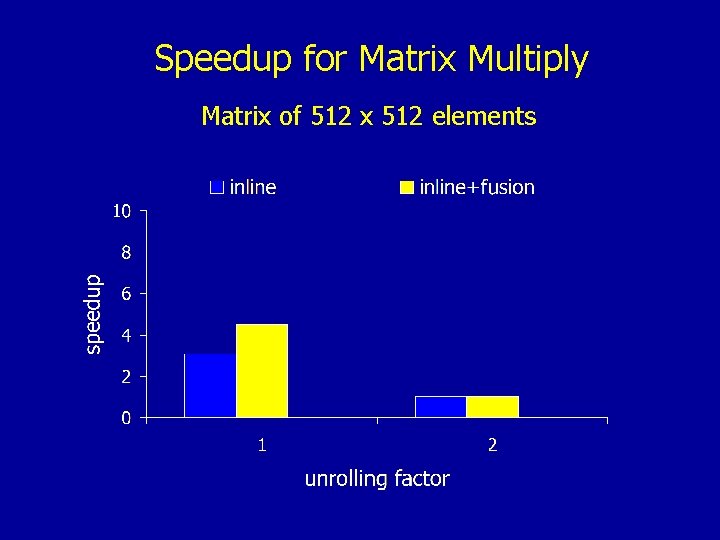
Speedup for Matrix Multiply Matrix of 512 x 512 elements

Speedup for Matrix Multiply Matrix of 512 x 512 elements

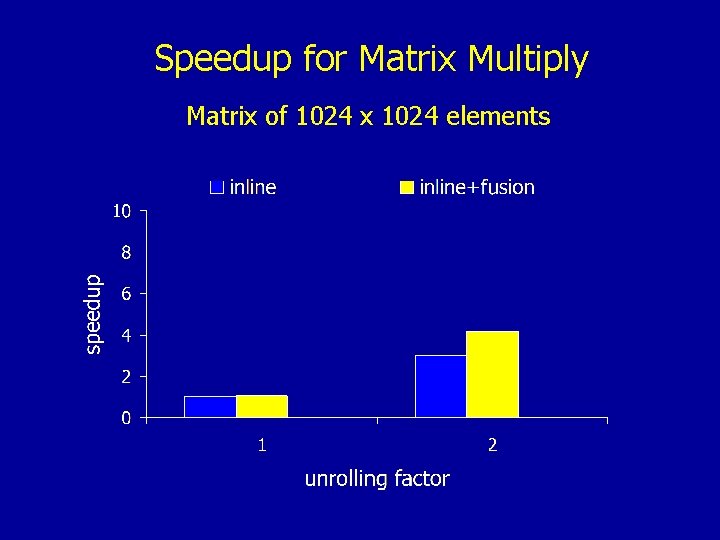
Speedup for Matrix Multiply Matrix of 1024 x 1024 elements

Efficiency of Unrolled Recursive Part • Because the recursive part is also unrolled, recursion may not exercise the large base cases • Which base case is executed depends on the size of the input problem • In our example: • For a problem of size n=8, the base case for n=1 is executed • For a problem of size n=16, the base case for n=2 is executed • The efficient base case for n=4 is not executed in these cases

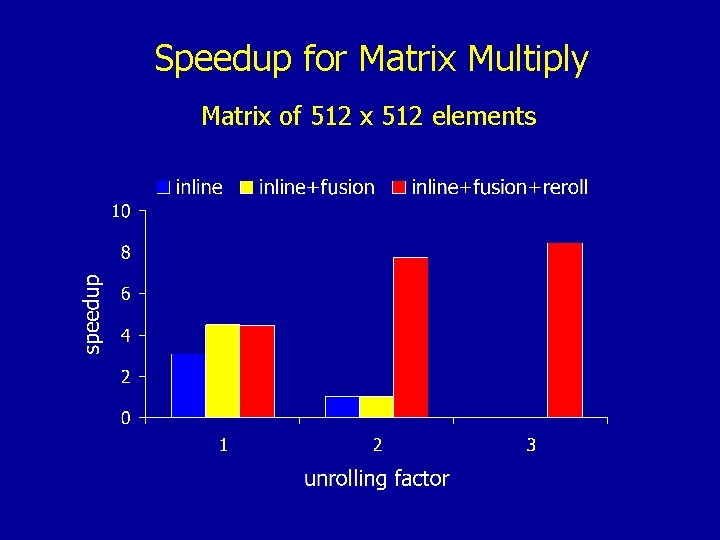
Solution: Recursion Re-Rolling • Roll back the recursive part of the unrolled procedure after the large base cases are generated • Re-Rolling ensures that larger base cases are always executed, independent of the input problem size • The compiler unrolls the recursive part only temporarily, to generate the base cases

Transformation 3: Recursion Re-Rolling void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else if (n/2/2 == 1) { *p += 1; *(p+n/2/2) += 1; *(p+n/2+n/2/2) += 1; } else { f 1(p, n/2/2/2); f 1(p+n/2/2/2, n/2/2/2); f 1(p+n/2/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2+n/2/2/2, n/2/2/2); }

Transformation 3: Recursion Re-Rolling Identify the recursive part void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else if (n/2/2 == 1) { *p += 1; *(p+n/2/2) += 1; *(p+n/2+n/2/2) += 1; } else { f 1(p, n/2/2/2); f 1(p+n/2/2/2, n/2/2/2); f 1(p+n/2/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2/2, n/2/2/2); f 1(p+n/2+n/2/2+n/2/2/2, n/2/2/2); }

Transformation 3: Recursion Re-Rolling Replace with the recursive part of the original procedure void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else if (n/2/2 == 1) { *p += 1; *(p+n/2/2) += 1; *(p+n/2+n/2/2) += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); }

Final Result void f 1(char *p, int n) if (n == 1) { *p += 1; } else if (n/2 == 1) { *p += 1; *(p+n/2) += 1; } else if (n/2/2 == 1) { *p += 1; *(p+n/2/2) += 1; *(p+n/2+n/2/2) += 1; } else { f 1(p, n/2); f 1(p+n/2, n/2); }

Speedup for Matrix Multiply Matrix of 512 x 512 elements

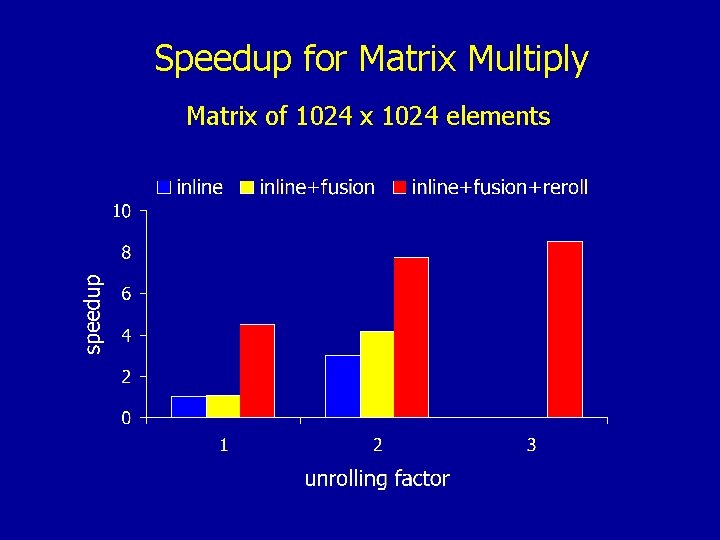
Speedup for Matrix Multiply Matrix of 1024 x 1024 elements

Other Optimizations • Inlining moves code from the inter-procedural level to the intra-procedural level • Conditional fusion brings code from the inter-basicblock level to the intra-basic-block level • Together, inlining and conditional fusion give subsequent compiler passes the opportunity to perform more aggressive optimizations

Comparison to Hand Coded Programs • Two applications: Matrix multiply, LU decomposition • Three machines: Pentium III, Origin 2000, Power. PC • Two different problem sizes • Compare automatically unrolled programs to optimized, hand coded versions from the Cilk benchmarks • Best automatically unrolled version performs: • Between 2. 2 and 2. 9 times worse for matrix multiply • As good as hand coded version for LU

Related Work • Procedure Inlining: • • • Scheifler (1977) Richardson, Ghanapathi (1989) Chambers, Ungar (1989) Cooper, Hall, Torczon (1991) Appel (1992) Chang, Mahlke, Chen, Hwu (1992)

Conclusion • Recursion Unrolling • analogous to the loop unrolling transformation • Divide and Conquer Programs • The programmer writes simple base cases • The compiler automatically generates large base cases • Key Techniques • Inlining: conceptually inline recursive calls • Conditional Fusion: simplify intra-procedural control flow • Re-Rolling: ensure that large base cases are executed




Comparison to Hand Coded Programs • Matrix multiply 512 x 512 elements: • Best automatically unrolled program: • Hand coded with three nested loops: • Hand coded Cilk program: 2. 55 sec. 3. 46 sec. 1. 16 sec. • Matrix multiply for 1024 x 1024 elements: • Best automatically unrolled program: • Hand coded with three nested loops: • Hand coded Cilk program: 20. 47 sec. 27. 40 sec. 9. 19 sec.

Correctness • Recursion unrolling preserves the semantics of the program: • The unrolled program terminates if and only if the original recursive program terminates • When both the original and the unrolled program terminate, the yield the same result

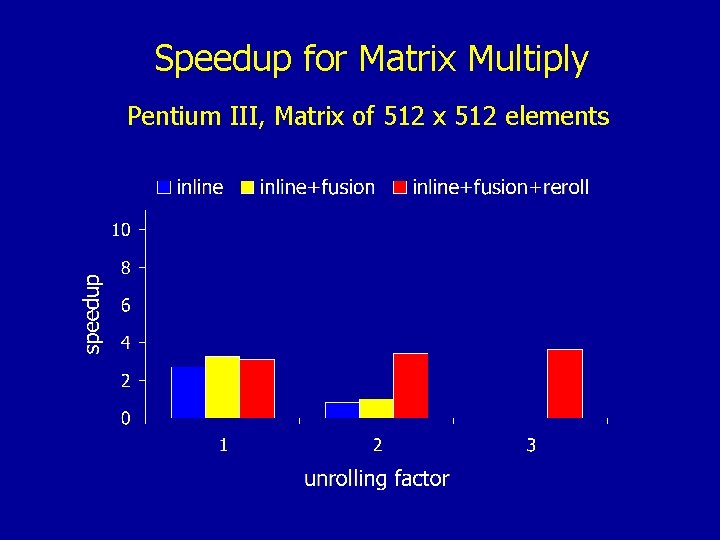
Speedup for Matrix Multiply Pentium III, Matrix of 512 x 512 elements

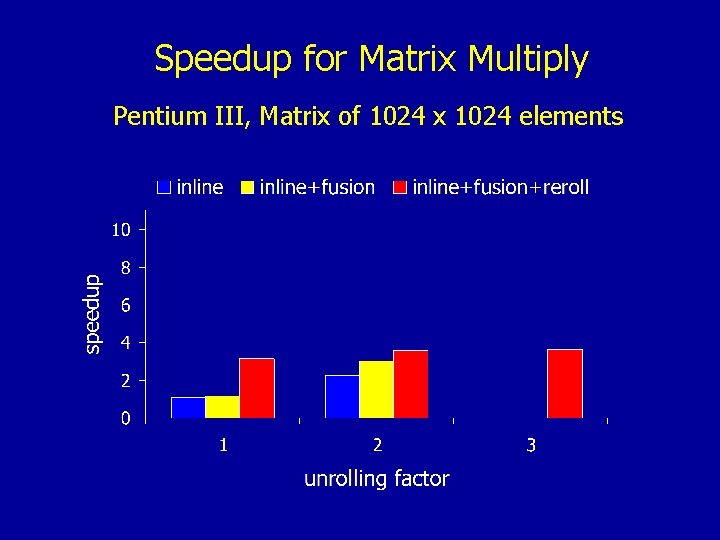
Speedup for Matrix Multiply Pentium III, Matrix of 1024 x 1024 elements

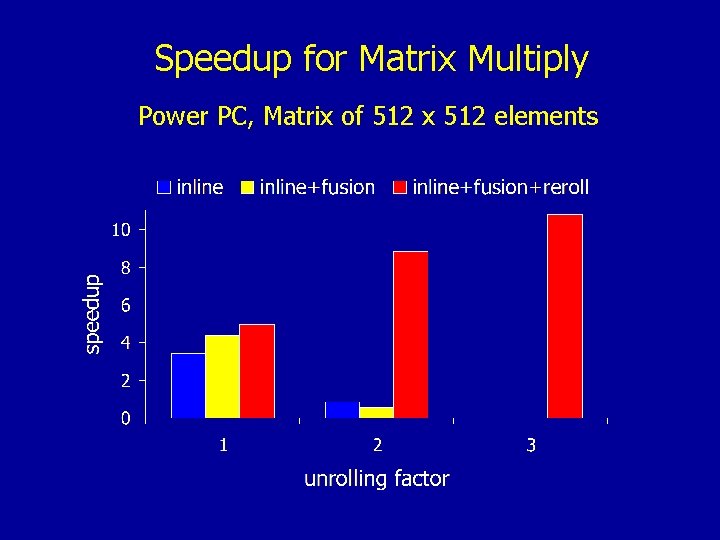
Speedup for Matrix Multiply Power PC, Matrix of 512 x 512 elements

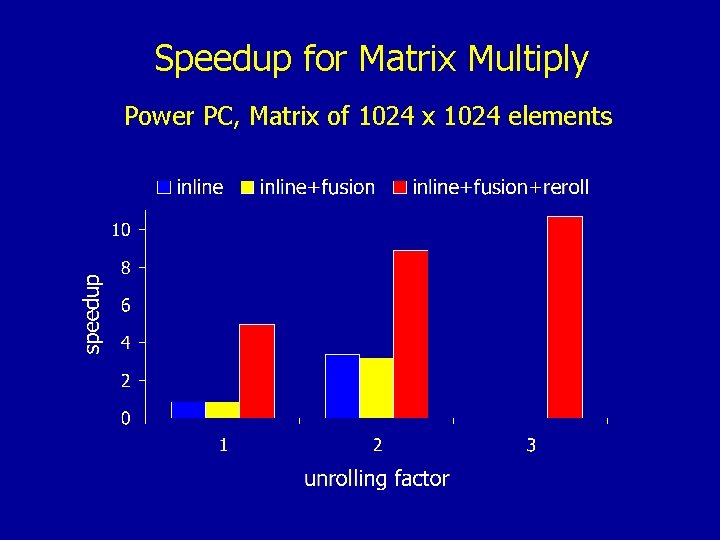
Speedup for Matrix Multiply Power PC, Matrix of 1024 x 1024 elements

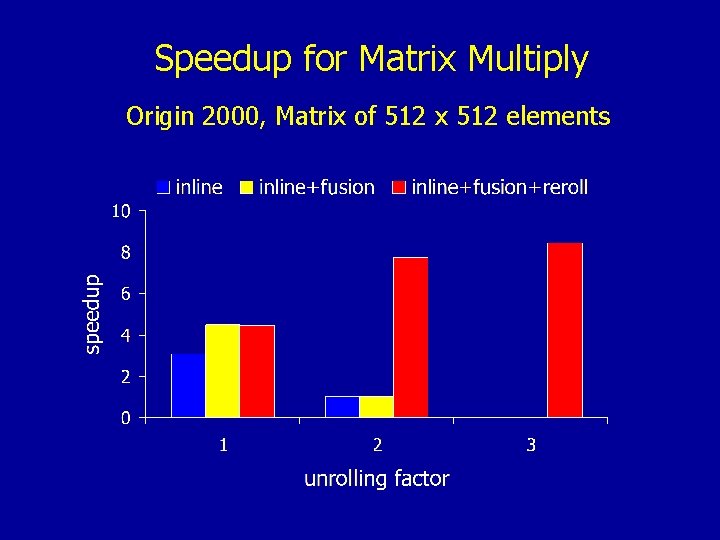
Speedup for Matrix Multiply Origin 2000, Matrix of 512 x 512 elements

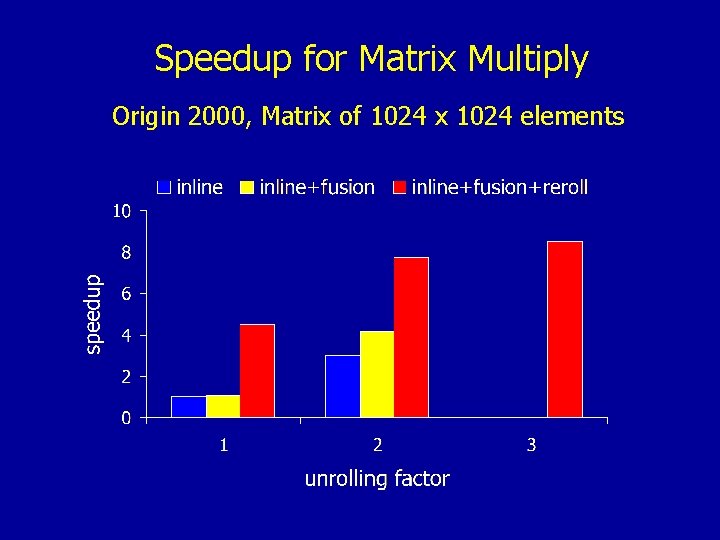
Speedup for Matrix Multiply Origin 2000, Matrix of 1024 x 1024 elements

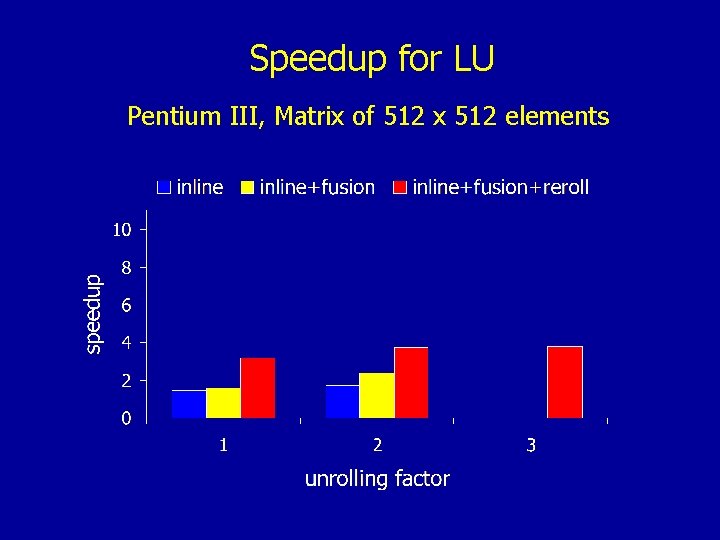
Speedup for LU Pentium III, Matrix of 512 x 512 elements

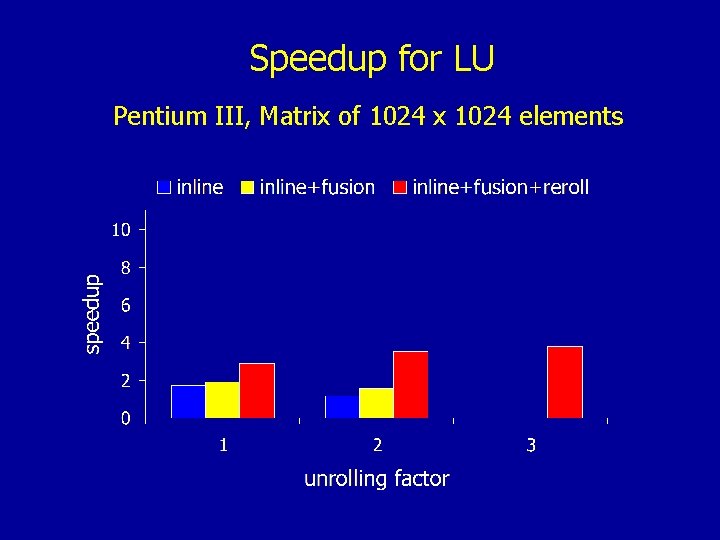
Speedup for LU Pentium III, Matrix of 1024 x 1024 elements

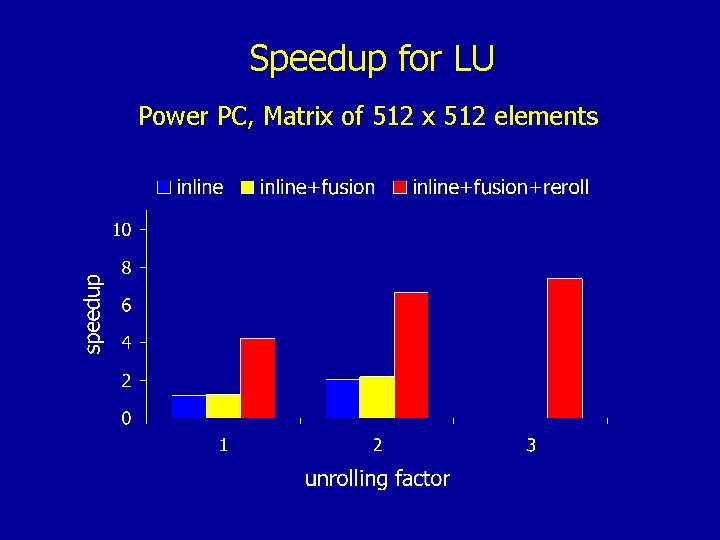
Speedup for LU Power PC, Matrix of 512 x 512 elements

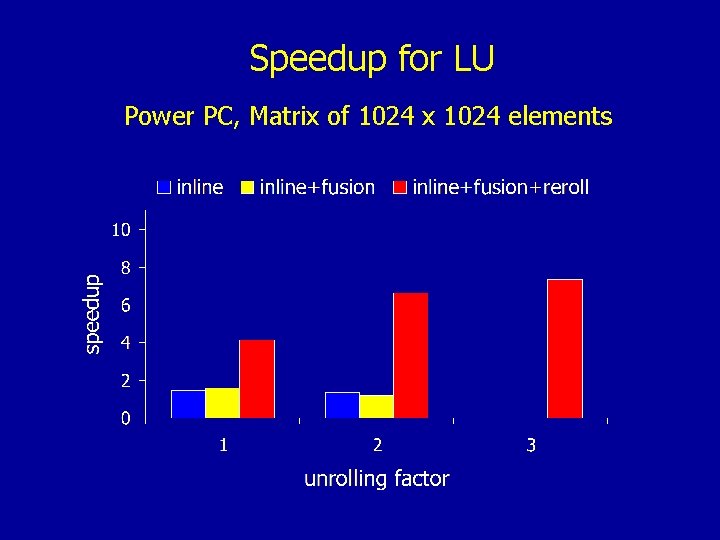
Speedup for LU Power PC, Matrix of 1024 x 1024 elements

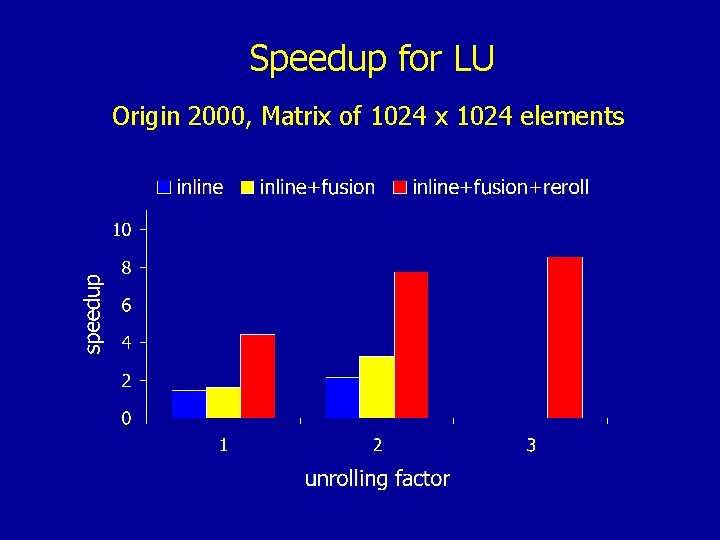
Speedup for LU Origin 2000, Matrix of 1024 x 1024 elements

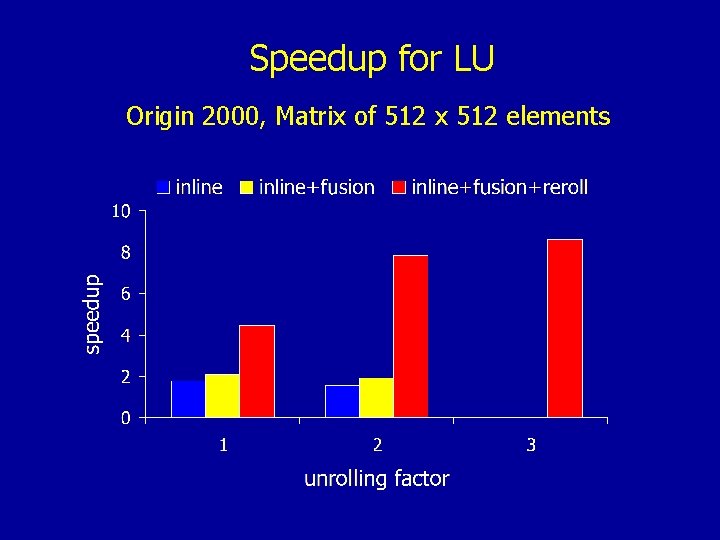
Speedup for LU Origin 2000, Matrix of 512 x 512 elements