RECURSION Self referential functions are called recursive i

RECURSION Self referential functions are called recursive (i. e. functions calling themselves) Recursive functions are very useful for many mathematical operations

Factorial: Recursive Functions 1! = 1 2! = 2*1! So: n! = n*(n-1)! For N>1 3! = 3*2*1 = 3*2! 1! = 1 4! = 4*3*2*1 = 4 * 3! Properties of recursive functions: 1) what is the first case (terminal condition) 2) how is the nth case related to the (n-1)th case Or more general: how is nth case related to <nth case

Recursive procedure A recursive task is one that calls itself. With each invocation, the problem is reduced to a smaller task (reducing case) until the task arrives at a terminal or base case, which stops the process. The condition that must be true to achieve the terminal case is the terminal condition.

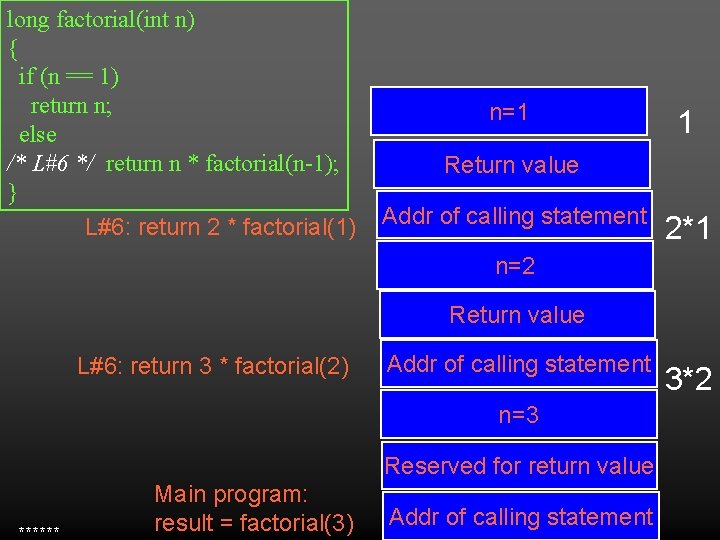
#include <iostream. h> long factorial(int); // function prototype int main() { int n; long result; cout << "Enter a number: "; cin >> n; result = factorial(n); cout << "n. The factorial of " << n << " is " << result << endl; return 0; } long factorial(int n) { Terminal condition to end recursion if (n == 1) return n; else return n * factorial(n-1); }

long factorial(int n) { if (n == 1) return n; else /* L#6 */ return n * factorial(n-1); } L#6: return 2 * factorial(1) n=1 1 Return value Addr of calling statement 2*1 n=2 Return value L#6: return 3 * factorial(2) Addr of calling statement n=3 Reserved for return value ****** Main program: result = factorial(3) Addr of calling statement 3*2

Iterative solution for factorial: int factorial (int n) { int fact; for (fact = 1; n>0; n--) fact=fact*n; return fact } Recursive functions can always be “unwound” and written iteratively

Example 2: Power function xn = 1 if n = 0 = x * xn-1 if n>0 53 = 5 * 52 52 = 5 * 51 51 = 5 * 50 50 = 1

Return 1 X=5, n=0 5 * power(5, 0) X=5, n=1 float power(float x, int n) { if (n == 0) return 1; else return x * power (x, n-1); } 5 * power(5, 1) X=5, n=2 5 * power(5, 2) X=5, n=3 Power(5, 3) ******

Power function xn Thus for n= 3, the recursive function is called 4 times, with n=3, n=2, n=1, and n=0 in general for a power of n, the function is called n+1 times. Can we do better?

We know that : x 14 = (x 7)2 x 7 = x (x 3)2 x 3 = x (x 1)2 x 1 = x (x 0)2 in other words: (x 7 * x 7) int (7/2) = 3 xn = 1 if n= 0 = x(xn/2)2 if n is odd = (xn/2)2 if n is even x 0 = 1 Floor of n/2

float power (float x, int n) { float Half. Power; //terminal condition if (n == 0) return 1; //can also stop at n=1 //if n Is odd if (n%2 == 1) { Half. Power = power(x, n/2); return (x * Half. Power *Half. Power): } else { Half. Power = power(x, n/2); return (Half. Power * Half. Power); ****

if (n == 0) return 1; if (n%2 == 1) { Half. Power = power(x, n/2); return (x * Half. Power *Half. Power): } else { Half. Power = power(x, n/2); return (Half. Power * Half. Power); } Can also use the call: return power(x, n/2) * power (x, n/2) But that is much less efficient!

Recursive Power Function: divide & conquer How many calls to the power function does the second algorithm make for xn? Log 2(n)!!!! **

Parts of a Recursive Function: recursive_function (…. N…. ) { //terminal condition 1. if (n == terminal_condition) return XXX; else { … recursive_function(…. <N…. ); 2. }

int main(void) { int z; z= f ( f(2) + f(5)); cout << z; } Recursion Example What gets printed? int f(int x) { int returnvalue; if (x==1) || (x== 3) return x; else return (x * f(x-1)) } (2 + 60)! / 2 **

Recursion: Example 4 Write a recursive boolean function to return True (1) if parameter x is a member of elements 0 through n of an array.

Int inarray(int a[], int n, int x) { if (n<0) return FALSE; else if (a[n] == x) return TRUE; else return inarray(a, n-1, x); }

What is a better name for this function? (i. e. , what does it do? ) int main() { int Randy. Jackson[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 99}; int *paula; paula = Randy. Jackson; American. Idol(paula); return 0; } int American. Idol(int *simon) { if (*simon == 99) return 0; American. Idol(simon+1); cout <<*simon<<endl; return 0; }

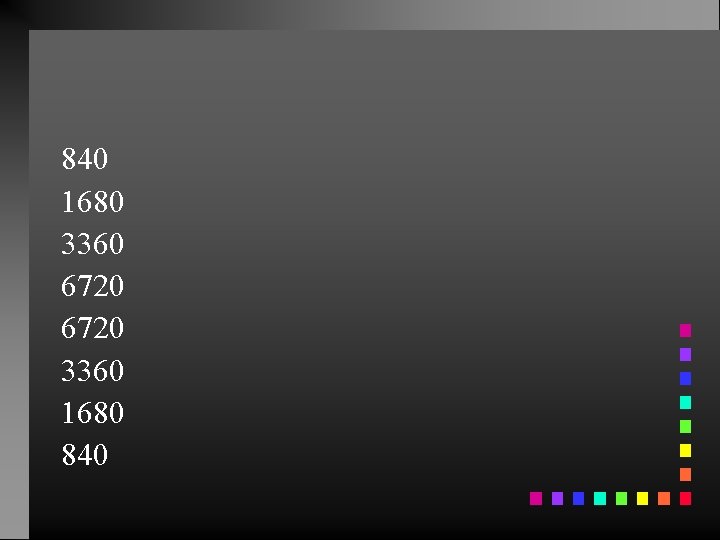
What gets printed? int r(int); int main () { r(840); return 0; } int r(int n) { cout << n <<endl; if (n <= 4242) r(2*n); cout << n << endl; return n; }

840 1680 3360 6720 3360 1680 840