Recursion Recursion is a fundamental programming technique that

  • Slides: 10
Download presentation
Recursion • Recursion is a fundamental programming technique that can provide an elegant solution

Recursion • Recursion is a fundamental programming technique that can provide an elegant solution certain kinds of problems © 2004 Pearson Addison-Wesley. All rights reserved 11 -1

Recursive Thinking • RECURSIVE algorithm: description for a way to solve a problem, that

Recursive Thinking • RECURSIVE algorithm: description for a way to solve a problem, that refers to itself • A method in Java can call itself; if written that way it is called a recursive method • A recursive method solves some problem. The code of recursive method should be written to handle the problem in one of two ways: § Base case: a simple case of the problem that can be answered directly; does not use recursion. § Recursive case: a more complicated case of the problem that isn’t easy to answer directly but can be expressed elegantly with recursion © 2004 Pearson Addison-Wesley. All rights reserved 11 -2

Recursive Definitions • Consider the following list of numbers: 24, 88, 40, 37 •

Recursive Definitions • Consider the following list of numbers: 24, 88, 40, 37 • Such a list can be defined as follows: A LIST is a: or a: number comma LIST • That is, a LIST is defined to be a single number, or a number followed by a comma followed by a LIST • The concept of a LIST is used to define itself © 2004 Pearson Addison-Wesley. All rights reserved 11 -3

Recursive Definitions • The recursive part of the LIST definition is used several times,

Recursive Definitions • The recursive part of the LIST definition is used several times, terminating with the non-recursive part: number comma LIST 24 , 88, 40, 37 number comma LIST 88 , 40, 37 number comma LIST 40 , 37 number 37 © 2004 Pearson Addison-Wesley. All rights reserved 11 -4

Recursive definitions • List of numbers: § 24 → 88→ 40→ 37/ • A

Recursive definitions • List of numbers: § 24 → 88→ 40→ 37/ • A list can be defined recursively: § LIST = null (EMPTY) § LIST = element → LIST © 2004 Pearson Addison-Wesley. All rights reserved 11 -5

Infinite Recursion • All recursive definitions have to have a nonrecursive part • If

Infinite Recursion • All recursive definitions have to have a nonrecursive part • If they didn't, there would be no way to terminate the recursive path • Such a definition would cause infinite recursion • This problem is similar to an infinite loop, but the non-terminating "loop" is part of the definition itself • The non-recursive part is often called the base case © 2004 Pearson Addison-Wesley. All rights reserved 11 -6

Recursive Definitions • N!, for any positive integer N, is defined to be the

Recursive Definitions • N!, for any positive integer N, is defined to be the product of all integers between 1 and N inclusive • This definition can be expressed NOT recursively as: 1! = 1 N! = N * (N-1) * (N-2) * … * 1 //NOT RECURSIVE Public static long factorial (int n) { long product = 1; for (int i=1; i<=n; i++) { product *= I; } Return product; } © 2004 Pearson Addison-Wesley. All rights reserved 11 -7

Recursive factorial Factorial can also be defined recursively: N! = N * (N-1)! •

Recursive factorial Factorial can also be defined recursively: N! = N * (N-1)! • A factorial is defined in terms of another factorial • Eventually, the base case of 1! is reached //RECURSIVE Public static long factorial (int n) { if (n== 0) { return 1; } else { return n * factorial (n-1); }} © 2004 Pearson Addison-Wesley. All rights reserved 11 -8

Recursive Definitions 5! 120 5 * 4! 24 4 * 3! 6 3 *

Recursive Definitions 5! 120 5 * 4! 24 4 * 3! 6 3 * 2! 2 * 1! 2 1 © 2004 Pearson Addison-Wesley. All rights reserved 11 -9

Fibonacci number • After two starting values, each number is the sum of the

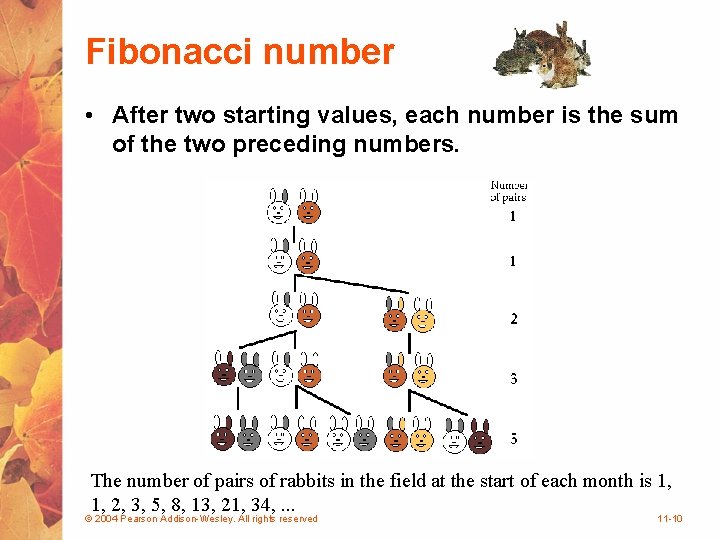
Fibonacci number • After two starting values, each number is the sum of the two preceding numbers. The number of pairs of rabbits in the field at the start of each month is 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . © 2004 Pearson Addison-Wesley. All rights reserved 11 -10

Recursion in Java recursion Recursion is the processRecursion in Java recursion Recursion is the process
Extra Practice for Recursion Recursion l Recursion isExtra Practice for Recursion Recursion l Recursion is
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
Recursion Search Recursion the Easy Solution Recursion isRecursion Search Recursion the Easy Solution Recursion is
Building Java Programs Chapter 12 Recursion Recursion recursionBuilding Java Programs Chapter 12 Recursion Recursion recursion
Recursion Recursion Recursion is the name given forRecursion Recursion Recursion is the name given for
Tail Recursion Problems with Recursion Recursion is generallyTail Recursion Problems with Recursion Recursion is generally
Tail Recursion Problems with Recursion Recursion is generallyTail Recursion Problems with Recursion Recursion is generally
Recursion Examples Recursion review Recursion review Scenario YouRecursion Examples Recursion review Recursion review Scenario You
Recursion CMSC 201 Recursion Vs Iteration Recursion andRecursion CMSC 201 Recursion Vs Iteration Recursion and
COSC 1 P 03 Recursion Recursion Recursion JustCOSC 1 P 03 Recursion Recursion Recursion Just
Data Structures Algorithms Recursion and Trees Recursion FundamentalData Structures Algorithms Recursion and Trees Recursion Fundamental
Turtle Technique The Turtle Technique is a techniqueTurtle Technique The Turtle Technique is a technique
Fundamental Programming Introduction to Functions Fundamental Programming 310201Fundamental Programming Introduction to Functions Fundamental Programming 310201
Fundamental Programming Testing Fundamental Programming 310201 1 ReviewFundamental Programming Testing Fundamental Programming 310201 1 Review
Fundamental Programming Data Processing and Expressions Fundamental ProgrammingFundamental Programming Data Processing and Expressions Fundamental Programming
Fundamental Programming for Loops Fundamental Programming 310201 RepetitionFundamental Programming for Loops Fundamental Programming 310201 Repetition
Fundamental Programming More Basics Fundamental Programming 310201 1Fundamental Programming More Basics Fundamental Programming 310201 1
Fundamental Derived Positions Fundamental derived Positions Fundamental derivedFundamental Derived Positions Fundamental derived Positions Fundamental derived
Recursion and Dynamic Programming Recursive thinking Recursion isRecursion and Dynamic Programming Recursive thinking Recursion is
Recursion Collections API Recursion Revisited Programming Assignments usingRecursion Collections API Recursion Revisited Programming Assignments using
Recursion Recursion is a powerful programming tool TheRecursion Recursion is a powerful programming tool The
Recursion Recursive Thinking Recursive Programming Recursion versus IterationRecursion Recursive Thinking Recursive Programming Recursion versus Iteration
Recursion Collections API Recursion Revisited Programming Assignments usingRecursion Collections API Recursion Revisited Programming Assignments using
Lecture 7 b Recursion is a fundamental programmingLecture 7 b Recursion is a fundamental programming
Recursion Canonical example factorial l Recursion l lRecursion Canonical example factorial l Recursion l l
Module 14 Recursion Module 14 Recursion Rosen 5Module 14 Recursion Module 14 Recursion Rosen 5
RECURSION Lecture 6 CS 2110 Spring 2013 RecursionRECURSION Lecture 6 CS 2110 Spring 2013 Recursion
Recursion You will learn the definition of recursionRecursion You will learn the definition of recursion
Using Recursion 2004 Goodrich Tamassia Using Recursion 1Using Recursion 2004 Goodrich Tamassia Using Recursion 1
CSCI 171 Presentation 7 Recursion What is recursionCSCI 171 Presentation 7 Recursion What is recursion
Recursion AP Computer Science A Recursion A methodRecursion AP Computer Science A Recursion A method
10 1 Description of Recursion Recursion When a10 1 Description of Recursion Recursion When a
Recursion Continued Tail Recursion versus Iterative Looping UsingRecursion Continued Tail Recursion versus Iterative Looping Using
Tree Recursion Traditional Approach Tree Recursion Consider theTree Recursion Traditional Approach Tree Recursion Consider the
Recursion Recursion Idea Some problems can be brokenRecursion Recursion Idea Some problems can be broken
Recursion You will learn the definition of recursionRecursion You will learn the definition of recursion
Recursion Aaron Tan Recursion http www comp nusRecursion Aaron Tan Recursion http www comp nus
Recursion KMITL 01076249 Data Structures Algorithms Recursion 1Recursion KMITL 01076249 Data Structures Algorithms Recursion 1
Recursion zyineleme Recursion zyineleme nedir Problemleri daha basitRecursion zyineleme Recursion zyineleme nedir Problemleri daha basit