Recursion Objectives Describe the concept of recursion Use

Recursion

Objectives • Describe the concept of recursion • Use recursion as a programming tool • Describe and use recursive form of binary search algorithm • Describe and use merge sort algorithm

Basics of Recursion: Outline • Basics of Recursion • Case Study: Digits to Words • How Recursion Works • Infinite Recursion • Recursive versus Iterative Methods • Recursive Methods that Return a Value

Basics of Recursion • A recursive algorithm will have one subtask that is a small version of the entire algorithm's task • A recursive algorithm contains an invocation of itself • Must be defined correctly else algorithm could call itself forever or not at all

Simple Example - Countdown • Given an integer value num output all the numbers from num down to 1 • Can do this easier and faster with a loop; the recursive version is an example only • First handle the simplest case; the base case or stopping condition

Recursive Countdown • Next handle larger cases; phrase solution in terms of a smaller version of the same problem • count. Down(3) is to output 3 then output the result of count. Down(2) public class Recursive. Countdown{ public static void main(String[] args){ count. Down(3); } public static void count. Down(int num){ if (num <= 0){ System. out. println(); } else { System. out. print(num); count. Down(num - 1); } } }
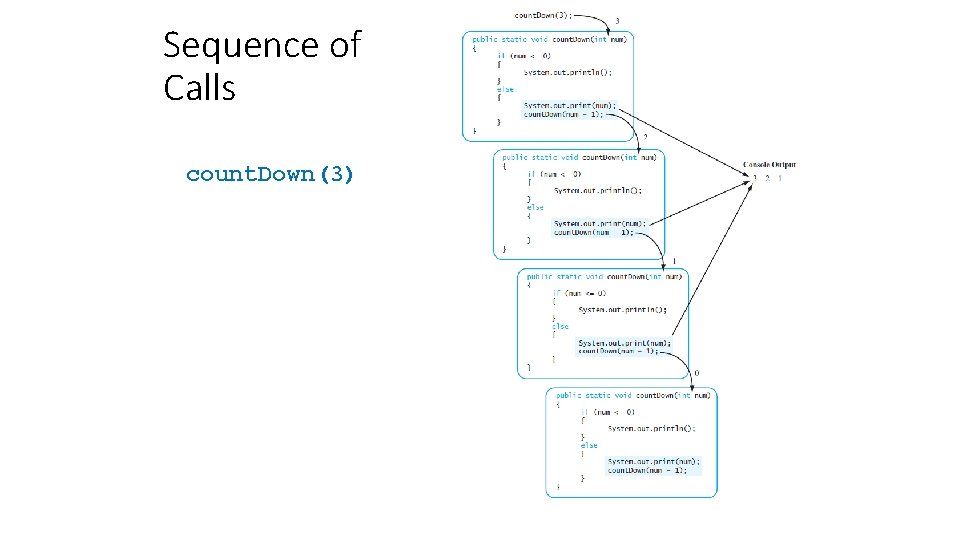
Sequence of Calls count. Down(3)

Case Study • Digits to Words – consider a method which receives an integer parameter • Then it prints the digits of the number as words • Heading

Case Study • Consider this useful private method

Case Study • If number has multiple digits, decompose algorithm into two subtasks 1. Display all digits but the last as words 2. Display last digit as a word First subtask is smaller version of original problem • • Same as original task, one less digit

Case Study • Algorithm for display. As. Words(number) 1. display. As. Words (number after deleting last digits) 2. System. out. print (get. Word. From. Digit(last digit of number + " ")

// Precondition: 0 <= digit <= 9 // Returns the word for the argument digit. private static String get. Word. From. Digit ( int digit) { String result = null; switch (digit) { case 0: result = "zero"; break; case 1: result = "one"; break; case 2: result = "two"; break; case 3: result = "three"; break; case 4: result = "four"; break; case 5: result = "five"; break; case 6: result = "six"; break; case 7: result = "seven"; break; case 8: result = "eight"; break; case 9: result = "nine"; break; default: System. out. println ("Fatal Error. "); System. exit (0); break; } return result; } import java. util. Scanner; public class Recursion. Demo { public static void main (String [] args) { System. out. println ("Enter an integer: "); Scanner keyboard = new Scanner (System. in); int number = keyboard. next. Int (); System. out. println ("The digits in that number are: "); display. As. Words (number); System. out. println ("If you add ten to that number, " ); System. out. println ("the digits in the new number are: " ); number = number + 10; display. As. Words (number); System. out. println (); } /** Precondition: number >= 0 Displays the digits in number as words. */ public static void display. As. Words (int number) { if (number < 10) System. out. print (get. Word. From. Digit (number) + " "); else //number has two or more digits { display. As. Words (number / 10); System. out. print (get. Word. From. Digit (number % 10) + " "); } } }
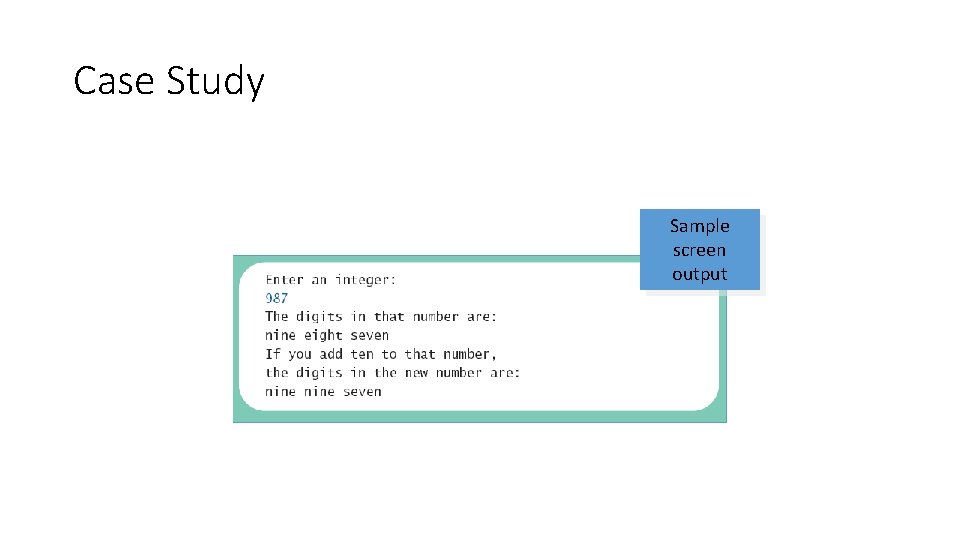
Case Study Sample screen output

How Recursion Works Executing recursive call

How Recursion Works Executing recursive call

How Recursion Works Executing recursive call

Keys to Successful Recursion • Must have a branching statement that leads to different cases • One or more of the branches should have a recursive call of the method • Recursive call must us "smaller" version of the original argument • One or more branches must include no recursive call • This is the base or stopping case

Infinite Recursion • Suppose we leave out the stopping case • Nothing stops the method from repeatedly invoking itself • Program will eventually crash when computer exhausts its resources (stack overflow)

Recursive Versus Iterative • Any method including a recursive call can be rewritten • To do the same task • Done without recursion • Non recursive algorithm uses iteration • Method which implements is iterative method • Note iterative version of program, class Iterative. Demo (Next Slide)

import java. util. Scanner; public class Iterative. Demo { public static void main (String [] args) < The rest of main is the same as in recursive version > /** Precondition: number >= 0 Displays the digits in number as words. */ public static void display. As. Words (int number) { int divisor = get. Power. Of. Ten (number); int next = number; while (divisor >= 10){ System. out. print (get. Word. From. Digit (next / divisor) + " "); next = next % divisor; divisor = divisor / 10; } System. out. print (get. Word. From. Digit (next / divisor) + " "); } // Precondition: n >= 0. // Returns 10 raised to the power n. private static int get. Power. Of. Ten (int n) { int result = 1; while (n >= 10) { result = result * 10; n = n / 10; } return result; } private static String get. Word. From. Digit (int digit) // The rest of get. Word. From. Digit is the same as in recursive verstion }

Recursive Versus Iterative • Recursive method • Uses more storage space than iterative version • Due to overhead during runtime • Also runs slower • However in some programming tasks, recursion is a better choice, a more elegant solution

Recursive Methods that Return a Value • Follow same design guidelines as stated previously • Second guideline also states • One or more branches includes recursive invocation that leads to the returned value import java. util. Scanner; public class Recursion. Demo 2{ public static void main (String [] args) { System. out. println ("Enter a nonnegative number: "); Scanner keyboard = new Scanner (System. in); int number = keyboard. next. Int (); System. out. println (number + " contains " + get. Number. Of. Zeros (number) + " zeros. "); } /** Precondition: n >= 0 Returns the number of zero digits in n. */ public static int get. Number. Of. Zeros (int n) { int result; if (n == 0) result = 1; else if (n < 10) result = 0; //n has one digit that is not 0 else if (n % 10 == 0) result = get. Number. Of. Zeros (n / 10) + 1; else //n % 10 != 0 result = get. Number. Of. Zeros (n / 10); return result; } }

Recursive Methods that Return a Value Sample screen output • Note recursive method Number. Of. Zeros • Has two recursive calls • Each returns value assigned to result • Variable result is what is returned

Programming with Recursion: Outline • Programming Example: Insisting that User Input Be Correct • Case Study: Binary Search

Case Study • Binary Search • We design a recursive method to tell whether or not a given number is in an array • Algorithm assumes array is sorted • First we look in the middle of the array • Then look in first half or last half, depending on value found in middle

Binary Search • Draft 1 of algorithm • Algorithm requires additional parameters
![Binary Search • Draft 2 of algorithm to search a[first] through a[last] • What Binary Search • Draft 2 of algorithm to search a[first] through a[last] • What](http://slidetodoc.com/presentation_image_h2/ba46cd2397e1cc44627fabaf7dd249a3/image-27.jpg)
Binary Search • Draft 2 of algorithm to search a[first] through a[last] • What if target is not in the array?
![Binary Search • Final draft of algorithm to search a[first] through a[last] to find Binary Search • Final draft of algorithm to search a[first] through a[last] to find](http://slidetodoc.com/presentation_image_h2/ba46cd2397e1cc44627fabaf7dd249a3/image-28.jpg)
Binary Search • Final draft of algorithm to search a[first] through a[last] to find target

Binary Search Binary search example

Binary Search Binary search example

Binary Search Binary search example

Binary Search /** Class for searching an already sorted array of integers. */ public class Array. Searcher{ private int [] a; //Precondition: the. Array is full and is sorted from lowest to highest. public Array. Searcher (int [] the. Array) { a = the. Array; //a is now another name for the. Array. } /** If target is in the array, returns the index of an occurrence of target. Returns -1 if target is not in the array. */ public int find (int target) { return binary. Search (target, 0, a. length - 1); } //Uses binary search to search for target in a[first] through //a[last] inclusive. Returns the index of target if target //is found. Returns -1 if target is not found. private int binary. Search (int target, int first, int last) { int result; if (first > last) result = -1; else { int mid = (first + last) / 2; if (target == a [mid]) result = mid; else if (target < a [mid]) result = binary. Search (target, first, mid - 1); else //(target > a[mid]) result = binary. Search (target, mid + 1, last); } return result; } }

Demo import java. util. Scanner; public class Array. Searcher. Demo{ public static void main (String [] args) { int [] an. Array = new int [10]; Scanner keyboard = new Scanner (System. in); System. out. println ("Enter 10 integers in increasing order, "); System. out. println ("one per line. "); for (int i = 0 ; i < 10 ; i++) an. Array [i] = keyboard. next. Int (); System. out. println (); for (int i = 0 ; i < 10 ; i++) System. out. print ("a[" + i + "]=" + an. Array [i] + " "); System. out. println (); Array. Searcher finder = new Array. Searcher (an. Array); String ans; do { System. out. println ("Enter a value to search for: "); int target = keyboard. next. Int (); int result = finder. find (target); if (result < 0) System. out. println (target + " is not in the array. "); else System. out. println (target + " is at index " + result); System. out. println ("Again? "); ans = keyboard. next (); } while (ans. equals. Ignore. Case ("yes")); System. out. println ("May you find what you're searching for. "); } }

Binary Search Sample screen output

Summary • Method with self invocation • Invocation considered a recursive call • Recursive calls • Legal in Java • Can make some method definitions clearer • Algorithm with one subtask that is smaller version of entire task • Algorithm is a recursive method

Summary • To avoid infinite recursion recursive method should contain two kinds of cases • A recursive call • A base (stopping) case with no recursive call • Good examples of recursive algorithms • Binary search algorithm • Merge sort algorithm
- Slides: 36