Recursion l Recursion means to define something in

Recursion l “Recursion" means to define something in terms of itself. l l A directory is a collection of files and directories. Words in dictionaries are defined in terms of other words. 1

Recursion l l l Like top down design, recursion breaks a problem into several smaller identical problems With recursion, these smaller problems are of exactly the same type as the original problem— mirror images! A recursive solution solves a problem by solving a smaller instance of the same problem! l l l It solves this new problem by solving an even smaller instance of the same problem. Eventually, the new problem will be so small that is solution will be either obvious or known. This solution will lead to the solution of the original problem 2

Recursion Vs Iteration l l l Recursion is an important problem solving approach that is an alternative to iteration An iterative solution involves loops Not all recursive solutions are better than iterative solutions, though. l l Some recursive solutions are impractical because they are so inefficient Recursion can provide elegantly simple solutions to problems of great complexity! 3

Printing a number in any base l What is 83790 in base 8? l l It's easy to find the last digit of a number n in base 8: It's simply n % 8. The remaining digits are then the representation of n / 8. 4

Solution Formulation print. Num. In. New. Base(num, base) { if (num is large or equal to base) { print. Num. In. New. Base (num / base, base) } //end if print the last digit of a number num in base } l l A recursive method calls itself – this action is what makes the solution recursive Each recursive call solves an identical, but smaller, problem A test for the base case enables the recursive calls to stop Eventually, one of the smaller problems must be the base case 5

Constructing Recursive Solutions l l How can you define the problem in terms of a smaller problem of the same type? How does each recursive call diminish the size of the problem? What in stance of the problem can save as the base case? As the problem size diminishes, will you reach this base case? 6

Printing a number in any base – Java Method private static final String DIGIT_TABLE = "0123456789 abcdef"; private static final int MAX_BASE = DIGIT_TABLE. length( ); // Print n in any base, recursively // Precondition: n >= 0, 2 <= base <= MAX_BASE private static void print. Num. In. New. Base(long n, int base) { if (n >= base) print. Num. In. New. Base(n / base, base); System. out. print(DIGIT_TABLE. char. At((int) (n % base))); } 7

Static Method - Recap l l A static method is a class method; it is invoked independently of any instance of the class that contains the method. Instances of the class share the static method, and if the static method is public, other objects can access it through the class name E. g. java. lang. Math. sqrt provides access to the static method sqrt contained in the class java. lang. Math Methods that don’t need access to instance variables and are self-contained (except for parameter input) are good candidates to be designed as static methods 8

Printing a number in any base - Why it works l l l Proof by induction on k, the number of digits of n in base b. If k = 1, then print. Num. In. New. Base prints one digit correctly (base case). Assume now that print. Num. In. New. Base works correctly for k digits. If we call print. Num. In. New. Base with a number n with k + 1 digits, then it recursively prints the first k digits correctly, followed by the last digit. It follows that print. Num. In. New. Base prints a k + 1 digit number correctly. 9

Correctness of recursive methods When arguing about the correctness of a recursive method, always assume that the recursive call works. l Of course there has to be a base case. l And we need to be sure that we will reach the base case -- there has to be some progress in each recursive call. l 10

The Factorial of n l l l The factorial problem has a simpler and efficient iterative solution, one would not use the recursive solution in practice! fact(n) = n*(n-1)*(n-2)*…*1, for any integer n > 0, fact(0) = 1 (iterative definition!) The factorial of a negative integer is undefined To define fact(n) recursively, need to define fact(n) in terms of a factorial of a smaller number fact(n) = n* [(n-1)*(n-2)*…*1] = n* fact(n-1) (a recurrence relation!) The base case is fact(0), which we know is 1. 11

A recursive definition of factorial fact(n) = 1 if n=0, n * fact(n-1) if n > 0 public static long fact(int n) { //computes the factorial of a nonnegative integer //Precondition: n must be greater than or equal to 0 //Postcondition: returns the factorial of n. if (n == 0) // base case return 1; else //Invariant: n > 0, so n-1 >= 0. //Thus, fact(n-1) returns (n-1)! return n * fact(n - 1); } //end fact 12

Mistakes l Why doesn't this work? public static long fact(int n) { return n * fact(n - 1); } l And this one? public static long fact(int n) { if (n <= 1) // base case return 1; else return n * fact(n); } 13

Recursive method evaluation l l l Theoretically, evaluating a recursive method is no more difficult than evaluating a nonrecursive method In practice, however, the bookkeeping can quickly get out of hand The box trace can be used as a systematic way to trace the actions of a recursive method l l Label each recursive call in the method (e. g. labeled A) Each time a method is called, a new box represents its local environment 14

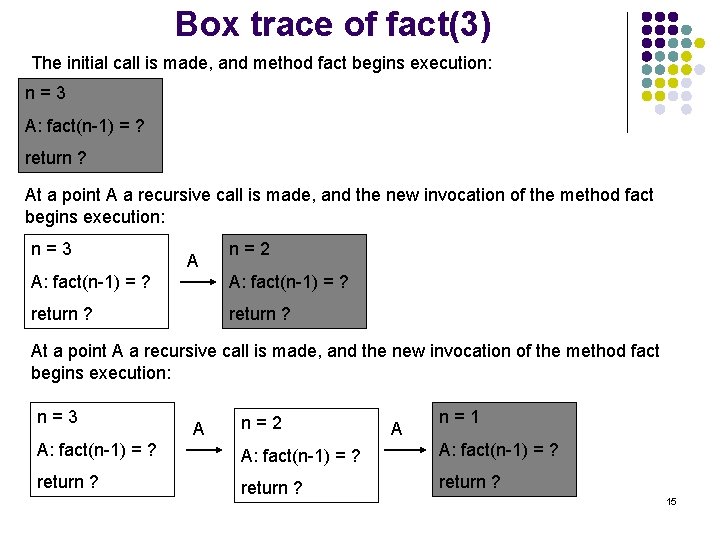
Box trace of fact(3) The initial call is made, and method fact begins execution: n=3 A: fact(n-1) = ? return ? At a point A a recursive call is made, and the new invocation of the method fact begins execution: n=3 A n=2 A: fact(n-1) = ? return ? At a point A a recursive call is made, and the new invocation of the method fact begins execution: n=3 A n=2 A n=1 A: fact(n-1) = ? return ? 15

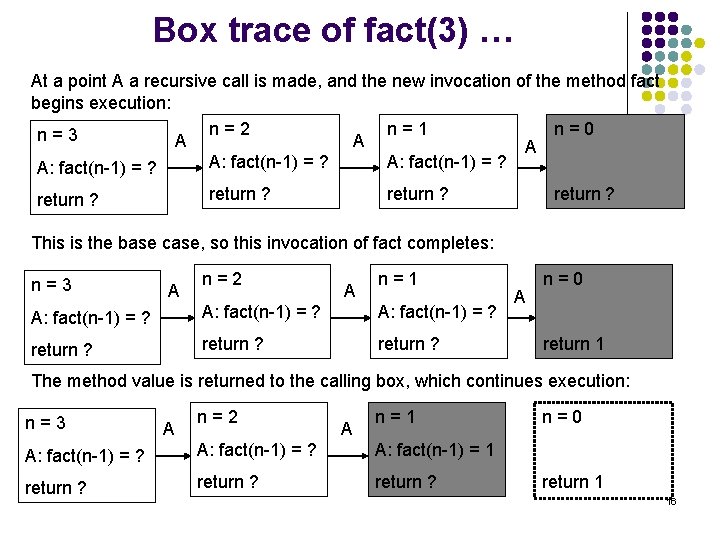
Box trace of fact(3) … At a point A a recursive call is made, and the new invocation of the method fact begins execution: n=2 n=1 n=0 n=3 A A: fact(n-1) = ? return ? This is the base case, so this invocation of fact completes: n=3 A n=2 A n=1 A: fact(n-1) = ? return ? A n=0 return 1 The method value is returned to the calling box, which continues execution: n=3 A n=2 A n=1 A: fact(n-1) = ? A: fact(n-1) = 1 return ? n=0 return 1 16

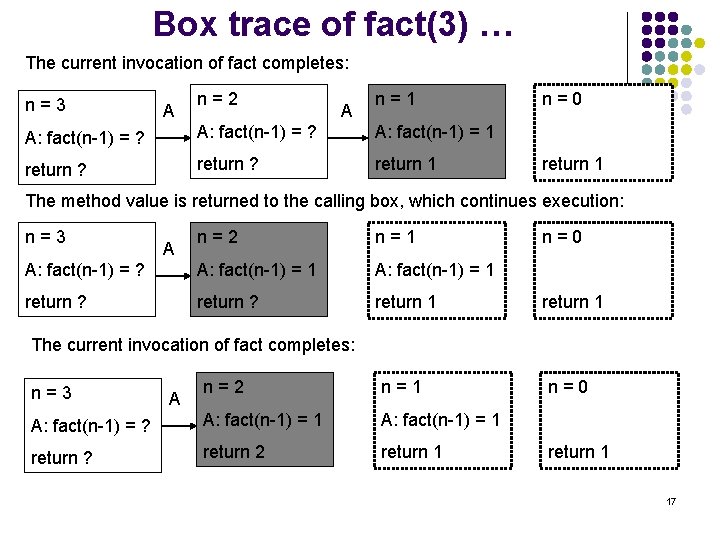
Box trace of fact(3) … The current invocation of fact completes: n=3 A n=2 A n=1 A: fact(n-1) = ? A: fact(n-1) = 1 return ? return 1 n=0 return 1 The method value is returned to the calling box, which continues execution: n=3 n=2 n=1 A: fact(n-1) = ? A: fact(n-1) = 1 return ? return 1 n=2 n=1 n=0 A: fact(n-1) = ? A: fact(n-1) = 1 return ? return 2 return 1 A n=0 The current invocation of fact completes: n=3 A return 1 17

Box trace of fact(3) … The method value is returned to the calling box, which continues execution: n=3 n=2 n=1 n=0 A: fact(n-1) = 2 A: fact(n-1) = 1 return ? return 2 return 1 n=0 The current invocation of fact completes: n=3 n=2 n=1 A: fact(n-1) = 2 A: fact(n-1) = 1 return 6 return 2 return 1 The value 6 is returned to the initial call. 18

Multiplying Rabbits(The fibonacci Sequence) l Assume recent survey “facts” states that: l l Rabbits never die A rabbit reaches sexual maturity exactly two months after birth Rabbits are always born in male-female pairs. At the beginning of every month, each sexually mature malefemale pair gives birth to exactly one male-female pair Suppose you started with a single new born malefemale pair. How many pairs would there be in month 6, counting the births that took place at the beginning of month 6? 19

Multiplying Rabbits(The fibonacci Sequence) l l To find rabbit(n) the number of pairs alive in month n, determine how you can use rabbit(n-1) to compute rabbit(n) is the sum of the number of pairs alive just prior to the start of month n and the number of pairs born at the start of month n. Just prior to the start of month n, there are rabbit(n-1) pairs of rabbits Not all of these rabbits are sexually mature at the start of month n. Only those who were alive in month n-2 are ready to reproduce at the start of month n 20

Multiplying Rabbits(The fibonacci Sequence) l l l Recurrence relation: rabbit(n) = rabbit(n-1) + rabbit(n-2) Now need to solve more than one smaller problem of the same type. Should be careful when selecting the base case Two base cases are necessary because there are two smaller problems of the same type rabbit(n) = 1 if n is 1 or 2, rabbit(n-1) + rabbit(n-2) if n > 2 l At best the method rabbit is inefficient! 21

Multiplying Rabbits - Too much recursion! public static int rabbit(int n) { //computes a term in the fibonacci sequence //Precondition: n is a positive integer //Postcondition: Return the nth Fibonacci number if ( n <= 2) { return 1; } else { // n > 2, so n – 1 > 0 and n-2 > 0 return rabbit(n-1) + (n-2); } //end if } //end rabbit l At best the method rabbit is inefficient! 22

Greatest Common Divisor 23

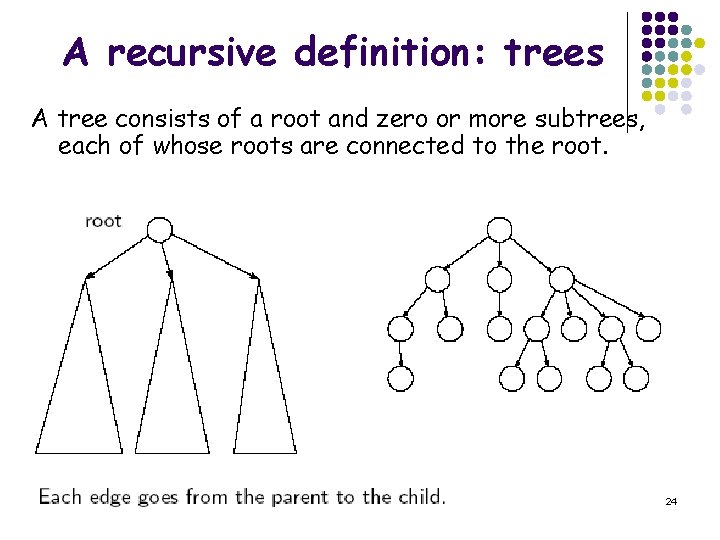
A recursive definition: trees A tree consists of a root and zero or more subtrees, each of whose roots are connected to the root. 24

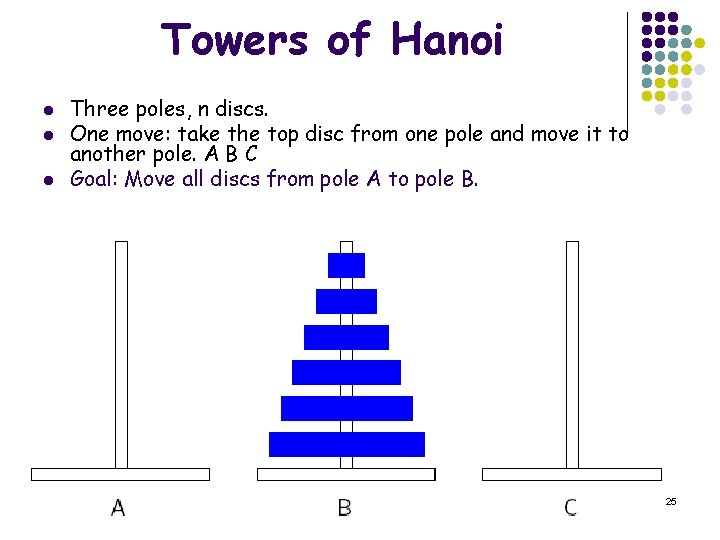
Towers of Hanoi l l l Three poles, n discs. One move: take the top disc from one pole and move it to another pole. A B C Goal: Move all discs from pole A to pole B. 25

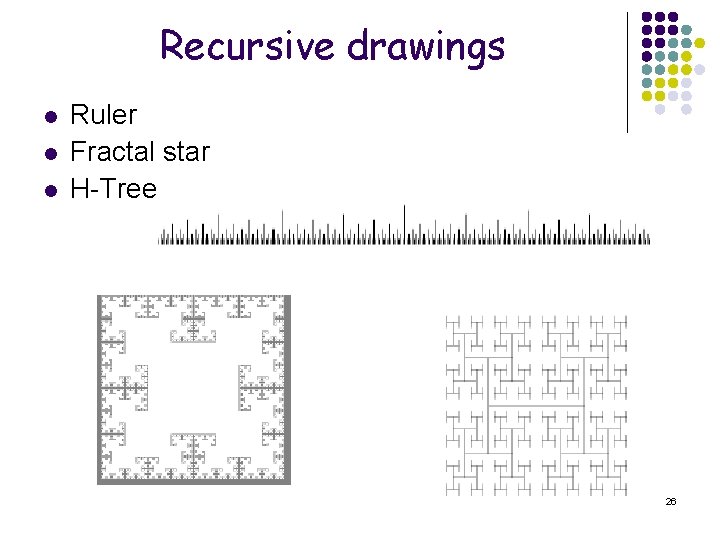
Recursive drawings l l l Ruler Fractal star H-Tree 26