Recursion l l Recursion means to recur or

Recursion l l Recursion – – means to recur or to repeat A different way to get a robot to repeat an action – within a new method we can send a simpler form of the same message using the same method name A programming language that allows recursive definitions (and not all do) – l Recursion is just another control structure, another programming tool to add to your collection

The Lost Beeper Mine problem l There is corner somewhere in the robot world that has a large number of beepers. The only clue to the location of this treasure is that somewhere, directly ahead of the robot, is a beeper. (There is no intervening wall segments. ) The Lost Mine is directly north of the beeper, a distance equal to the number of moves the robot makes to get from its current position to the beeper. l Download Prospector. zip demo.

How does this work? l Finding the beeper? void find. Beeper() { if (! next. To. ABeeper() ) { move(); find. Beeper(); } } l l // robot next to beeper // go to next corner // is the beeper here? In order to find the beeper, we define the method find. Beeper() that calls itself to help finish the search This is a recursive definition

Recursive Definitions l We do not define a method in terms of precisely itself – – We define a thing in terms of a simpler, or smaller version of itself Here we define find. Beeper() as l l – – either “nothing” (if the robot is on the corner with a beeper) or “move(); find. Beeper() ” It is also necessary to know that a beeper does lie in the robot’s path, or we fall into infinite recursion Every call results in a separate instance of the instruction find. Beeper();

Lost Beeper Mine, again l l So we have a sense of how we found the position-marker beeper How did we get to the mine? At every place we called a simpler version of find. Mine(), we were leaving some unfinished work behind A recursive method, as any other method. Must complete its task before control is returned to the call-site of the method (where the method was called from)

find. Mine() void find. Maine() { if (next. To. ABeeper()) { // found beeper turn. Left() // we know the mine is north of us } else { move(); // still looking for beeper find. Mine(); // next method call (call-site) move(); // unfinished business } } l l The “unfinished business” must be completed for each recursive call before each method is done. It is actually this unfinished business that correctly propels us to the lost mine

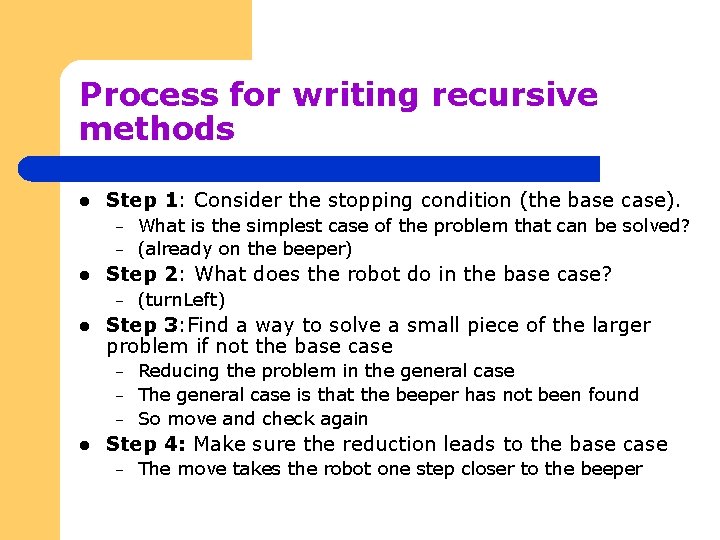
Process for writing recursive methods l Step 1: Consider the stopping condition (the base case). – – l Step 2: What does the robot do in the base case? – l (turn. Left) Step 3: Find a way to solve a small piece of the larger problem if not the base case – – – l What is the simplest case of the problem that can be solved? (already on the beeper) Reducing the problem in the general case The general case is that the beeper has not been found So move and check again Step 4: Make sure the reduction leads to the base case – The move takes the robot one step closer to the beeper

Iteration vs Recursion l l An iterative loop completes each cycle before beginning the next one A recursive method begins a new instance before completing the current one – – – l The current instance is temporarily suspended The second instance might be suspended as it calls another Each successive instance must be completed in turn, last to first Each recursive method is supposed to make minimal progress toward the base case, it will never be controoled by a loop, but by some form of the IF instruction

Tail Recursion l Tail recursion: Form of recursion in which the recursive call is the last instruction in the method void pick. All. Beepers() { if (next. To. ABeeper()) { pick. Beeper(); pick. All. Beepers(); } } // recursive call

Tail Recursion and WHILE loops void pick. All. Beepers() { if (next. To. ABeeper()) { pick. Beeper(); pick. All. Beepers(); // recursive call } } l Execution equivalent with void pick. All. Beepers() { while (next. To. ABeeper()) { pick. Beeper(); } }

WHILE loop a special form of recursion l l A formal definition of the WHILE loop We are going to discuss and analyze instructions (the meta-level), not use them – – – l W is the while statement T is the test L is the instruction list The formal definition of W is – – W == if (T){L; W; } Notice that the WHILE statement W is defined in terms of itself

Loop verification l An informal way to reason about loop correctness – – l Show that instruction works when the initial situation results in the test being false Show that each time the loop body is executed, the robot’s new situation is a sompler and similar version of the old situation We need a formal way of thinking about loops to verify that they are correct

Loop Invariants l l A key concept Definition: an assertion which is true after each iteration of a loop – l Assertion: something that can be demonstrated as being true or false For our purposes (the study of robots) – Loop invariants will be assertions about the robot’s world

After one iteration we consider: l l Has the direction the robot is facing changed? (How? ) Has the robot’s relative position in the world changed? (How? ) – l l This may involve thinking about wall segments Has the number of beepers in the beeper bag changed? (How? ) Has the number and location of other beepers in the world changed? (How? )

clear. All. Beepers. To. The. Wall() while (front. Is. CLear()) { move(); pick. Beeper(); } l What can we assert? – – l Direction is unchanged Position advanced one corner New corner has one less beeper Beeper-bag has one more beeper Bold, italic assertions are interesting – Interesting means which items are important for the problem being solved

Interesting assertions l l A loop invariant captures the interesting change during one iteration of the loop clear. All. Beepers. To. The. Wall() invariant: – l What else have we learned? – l Robot has advanced one corner and removed one beeper from that corner When the loop ends the front will be blocked Therefore, after the loop, the robot will have removed one beeper from each corner it has passed, and the robot’s front is blocked – As long as each corner has one beeper on it, the loop has solved the problem of picking up beepers to the wall

Uses for loop invariants l For analysis (we have done this) – – – l Powerful tools in aiding our understanding of how a loop is operating and what it will cause a robot to do Key: How does the robot change the state of the world? Once we know the invariant, we can use it and the terminating condition to determine if the loop solves the problem For building loops (we will do this next) – What instructions do we want to use in a loop body?

find. Beeper(): Problem statement l A robot is searching for a beeper that is an unknown distance directly in front of it and there may be one-block long wall segments in the way l What should be true when the loop terminates? – l Next to a beeper What is the invariant – The robot has moved one and only one block forward so that each corner can be inspected

find. Beeper(): First Pass While (! next. To. ABeeper()) { move(); } l l Terminating condition is correct Problem with the body – – Will this maintain the invariant? But what situations may be true in the world that could cause errorshutoffs?

find. Beeper(): Second Pass While (! next. To. ABeeper()) { if (front. Is. Clear()) { move(); } else { avoid. Wall(); } } l l Terminating condition is correct Does this correct the body? – – l Will this maintain the invariant? Does this handle the problem of the wall segments ? In designing avoid. Wall() we must keep the loop invariant in mind – Make sure the robot advances only one corner