Recursion is a concept of defining a method

Recursion is a concept of defining a method that makes a call to itself. Trees 1

Recursion is a concept of defining a method that makes a call to itself. Trees 2

Factorial Example: f(n)=n!=n×(n-1)×(n-2)×…× 2× 1 Initialization: f(0)=1 Recursive Call: f(n)=n×f(n-1) and. Java code: public static int recursive. Factorial(int n) { if (n==0) return 1; else return n*recursive. Factorial(n-1); } Trees 3

Fibonacci sequence: {fn } = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … Initialization: f 0 = 0, f 1 = 1 Recursive Call: fn = fn-1+fn-2 for n > 1. Java code: public static int recursive. Fibonacci(int n) { if (n==0) return 0; if (n==1) return 1; else return recursive. Fibonacci(n-1)+recursive. Fibonacci (n-2); } L 16 4

A={4, 3, 6, 2, 5} Linear. Sum return 15+A[4]=20 Algorithm Linear. Sum(A, n) Linear. Sum(A, 5) return 13+A[3]=15 Input: an integer array A of n elements Output: The sum of the n elements Linear. Sum(A, 4) return 7+A[2]=13 if n=1 then Linear. Sum(A, 3) return A[0] return 4+A[1]=7 return Linear. Sum(A, n-1)+A[n-1] • The recursive method should always Linear. Sum(A, 2) possess—the method terminates. • We did it by setting : • ” if n=1 then return A[0] ” f(n)=A[n-1]+f(n-1) for n>0 and f(1)=A[0] Trees return A[0]=4 Linear. Sum(A, 1) The compiler of any high level computer language uses a stack to handle recursive calls. 5

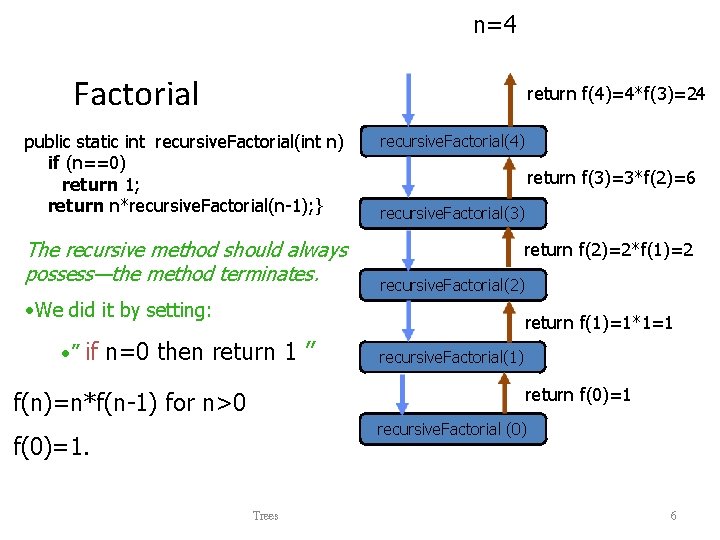
n=4 Factorial return f(4)=4*f(3)=24 public static int recursive. Factorial(int n) if (n==0) return 1; return n*recursive. Factorial(n-1); } The recursive method should always possess—the method terminates. recursive. Factorial(4) return f(3)=3*f(2)=6 recursive. Factorial(3) return f(2)=2*f(1)=2 recursive. Factorial(2) • We did it by setting: return f(1)=1*1=1 • ” if n=0 then return 1 ” recursive. Factorial(1) return f(0)=1 f(n)=n*f(n-1) for n>0 recursive. Factorial (0) f(0)=1. Trees 6

Fibonacci sequence public static int recursive. Fibonacci(int n) { if (n==0) return 0; if (n==1) return 1; return recursive. Fibonacci(n-1) +recursive. Fibonacci (n-2); } L 16 7

Reverse. Array Algorithm Reverse. Array(A, i, j): input: An array A and nonnegative integer indices i and j output: The reversal of the elements in A starting at index i and ending at j if i<j then A={1, 2, 3, 4}. { Reverse. Array(A, 0, 3) swap A[i] and A[j] Reverse. Array(A, i+1, j-1)} A={4, 2, 3, 1} } What is the base case? Reverse. Array(A, 1 2) A=(4, 3, 2, 1} Trees 8

Find. Max Algorithm Find. Max(A, i, j): input: Array A , indices i and j, i≤j output: The maximum element starting i and ending at j if i<j then 1 { a←Find. Max(A, i, (i+j)/2) T(n/2)+1 b←Find. Max(A, (i+j)/2+1, j) T(n/2)+1 return max(a, b) 1 } return A[i] 1 Trees Running time: T(n)=2 T(n/2)+c 1 T(1)=c 2 where c 1 and c 2 are some constants. T(n)=2 T(n/2)+c 1 =2[2 T(n/4)+c 1]+c 1 =4 T(n/4)+3 c 1 =… =2 k. T(1)+(1+2+4+… 2 k)c 1 =n. T(1)+2 k+1 c 1 =O(n) 9

Binary Search Algorithm Binary. Search(A, i, j, key): input: Sorted Array A , indices i and j, i≤j, and key output: If key appears between elements from i to j, inclusively if i≤j mid (i + j) / 2 if A[mid] = key return mid if A[mid] < key return Binary. Search(A, mid+1, j, key) else return Binary. Search(A, i, mid-1, key) return -1 Trees Running time: T(n)=T(n/2)+c 1 T(1)=c 2 where c 1 and c 2 are some constants. T(n)=T(n/2)+c 1 =[T(n/4)+c 1]+c 1 =T(n/4)+2 c 1 =… =T(1) + kc 1 =? 10