Recursion Chapter 12 12 1 Nature of Recursion

Recursion Chapter 12

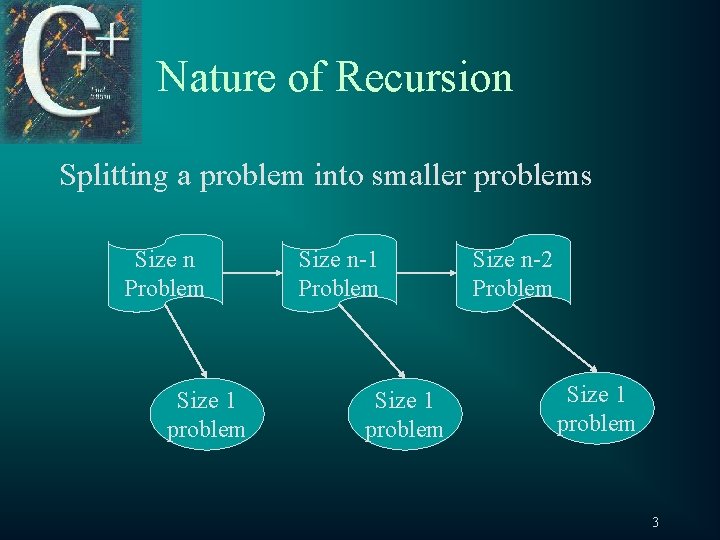
12. 1 Nature of Recursion t Problems that lend themselves to a recursive solution have the following characteristics: – One or more simple case of the problem have a straightforward, non-recursive solution – Otherwise, use reduced cases of the problem that are closer to a stopping case – Eventually the problem can be reduced to stopping cases only. Easy to solve 2

Nature of Recursion Splitting a problem into smaller problems Size n Problem Size 1 problem Size n-1 Problem Size 1 problem Size n-2 Problem Size 1 problem 3

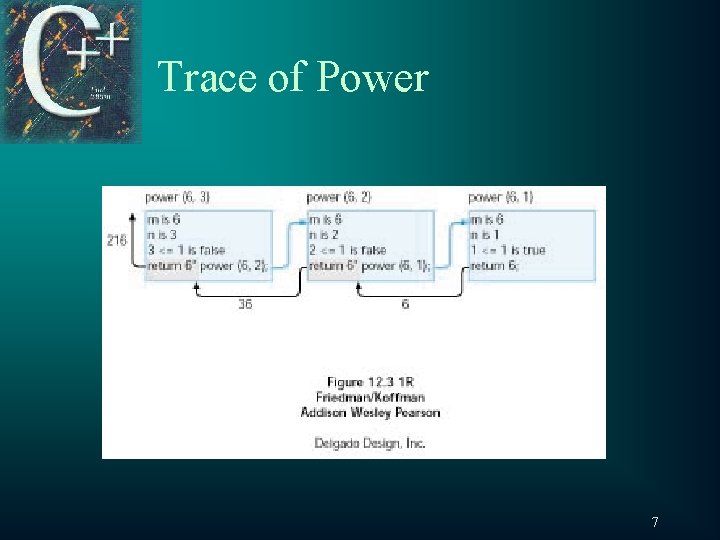
Power by Multiplication t Raise 6 to the power of 3 – Raise 6 to the power of 22 – Multiply the result by 6 t Raise 6 to the power of 2 – Raise 6 to the power of 1 – Multiply the result by 6 t Multiplying 6 * 6 4

Power. cpp // FILE: Power. cpp // RECURSIVE POWER FUNCTION // Raises its first argument to the power // indicated by its second argument. // Pre: m and n are defined and > 0. // Post: Returns m raised to power n. int power (int m, int n) { if (n <= 1) return m; else return m + power (m, n - 1); } 5

12. 2 Tracing Recursive Functions t t t Hand tracing we see how algorithm works Very useful in recursion Previous Multiply example trace “Activation Frame” corresponds to a function call Darker shading shows the depth of recursion 6

Trace of Power 7

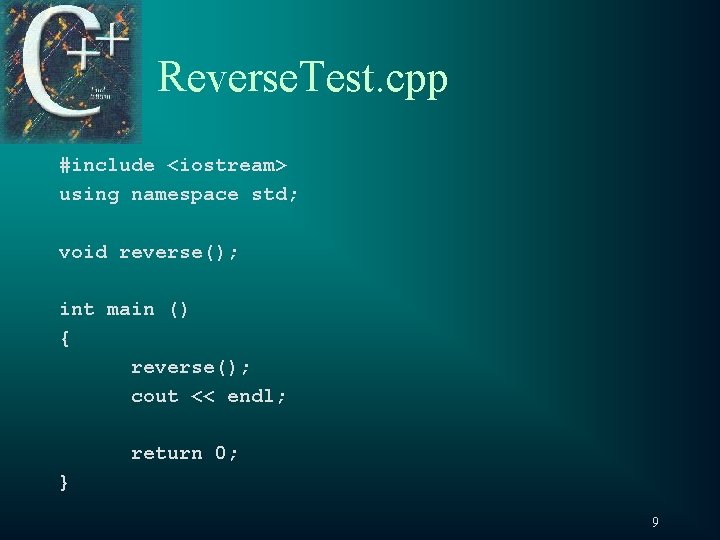
Recursive Function with No Return Value t If statement with some stopping condition – n <= 1; t When TRUE stopping case is reached – recursive step is finished – falls back to previous calls (if any) – trace of reverse t Reverse. Test. cpp 8

Reverse. Test. cpp #include <iostream> using namespace std; void reverse(); int main () { reverse(); cout << endl; return 0; } 9

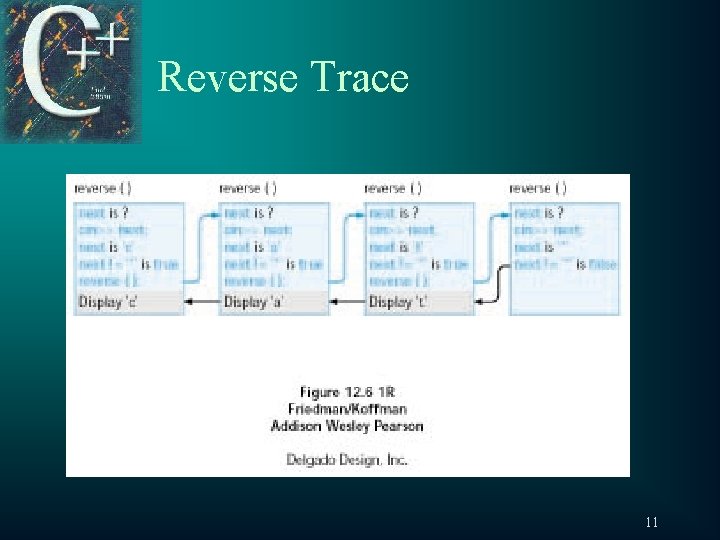
Reverse. Test. cpp void reverse() { char next; cout << "Next character or * to stop: "; cin >> next; if (next != ‘*’) { reverse(); cout << next; } } 10

Reverse Trace 11

Argument and Local Variable Stacks t t t How does C++ keep track of n and next ? Uses a data structure called a stack Think of a stack of trays in a cafeteria Each time a function is called it is pushed onto the stack Only top values are used when needed (popping) Example of calls to reverse 12

Recursive String t After 1 st call to reverse n next 3 ? top – c is read into next just prior to 2 nd call n next 3 c top 13

Recursive String t After 2 nd call to reverse n next 2 ? top 3 c – letter a is read into next just prior to 3 rd call n next 2 a top 3 c 14

Recursive String t After 3 rd call to reverse n next 1 ? top 2 a 3 c – letter t is read into next printed due to stop case n next 1 t top 2 a 3 c 15

Recursive String t After 1 st return n 2 3 t top After 2 nd return n 3 t next a c next c After 3 rd return (final) ? ? 16

12. 3 Recursive Mathematical Functions t Many mathematical functions are defined recursively – factorial n! of a number – 0! = 1 – n! = n * *n-1)! for n > 0 – So 4! = 4 * 3 * 2 * 1 or 24 t Look at a block of recursive math function example source code files 17

Factorial. cpp // FILE: Factorial. cpp // RECURSIVE FACTORIAL FUNCTION // COMPUTES N! int factorial (int n) { if (n <= 0) return 1; else return n * factorial (n-1); } 18

Factorial Trace 19

Factorial. I. cpp // FILE: Factorial. I. cpp // ITERATIVE FACTORIAL FUNCTION // COMPUTES N! int factorial. I (int n) { int factorial; factorial = 1; for (int i = 2; i <= n; i++) factorial *= i; return factorial; } 20

Fibonacci. cpp // FILE: Fibonacci. cpp // RECURSIVE FIBONACCI NUMBER FUNCTION int fibonacci (int n) // Pre: n is defined and n > 0. // Post: None // Returns: The nth Fibonacci number. { if (n <= 2) return 1; else return fibonacci (n - 2) + fibonacci (n - 1); } 21

GCDTest. cpp // FILE: gcd. Test. cpp // Program and recursive function to find // greatest common divisor #include <iostream> using namespace std; // Function prototype int gcd(int, int); 22

GCDTest. cpp int main() { int m, n; // the two input items cout << "Enter two positive integers: "; cin >> m >> n; cout << endl; cout << "Their greatest common divisor is " << gcd(m, n) << endl; return 0; } 23

GCDTest. cpp // // // Finds the greatest common divisor of two integers Pre: m and n are defined and both are > 0. Post: None Returns: The greatest common divisor of m and n. int gcd(int m, int n) { if (m < n) return gcd(n, m); 24

GCDTest. cpp else if (m % n == 0) return n; else return gcd(n, m % n); // recursive step } 25

GCDTest. cpp Program Output Enter two positive integers separated by a space: 24 84 Their greatest common divisor is 12 26

12. 4 Recursive Functions with Array Arguments // File: find. Sum. Test. cpp // Program and recursive function to sum an // array's elements #include <iostream> using namespace std; // Function prototype int find. Sum(int[], int); int bin. Search(int[], int, int); 27

Find. Sum. Test. cpp int main() { const int SIZE = 10; int x[SIZE]; int sum 1; int sum 2; // Fill array x for (int i = 0; i < SIZE; i++) x[i] = i + 1; 28

Find. Sum. Test. cpp // Calulate sum two ways sum 1 = find. Sum(x, SIZE); sum 2 = (SIZE * (SIZE + 1)) / 2; cout << "Recursive sum is " << sum 1 << endl; cout << "Calculated sum is " << sum 2 << endl; cout << bin. Search(x, 10, SIZE-1) << endl; return 0; } 29

Find. Sum. Test. cpp // Finds the sum of integers in an n-element // array int find. Sum(int x[], int n) { if (n == 1) return x[0]; else return x[n-1] + find. Sum(x, n-1); } 30

Find. Sum. Test. cpp // // // Searches for target in elements first through last of array Precondition : The elements of table are sorted & first and last are defined. Postcondition: If target is in the array, return its position; otherwise, returns -1. int bin. Search (int table[], int target, int first, int last) { int middle; 31

Find. Sum. Test. cpp middle = (first + last) / 2; if (first > last) return -1; else if (target == table[middle]) return middle; else if (target < table[middle]) return bin. Search(table, target, first, middle-1); else return bin. Search(table, target, middle+1, last); } 32

12. 5 Problem Solving with Recursion t t Case Study: The Towers of Hanoi Problem Statement – Solve the Towers of Hanoi problem for n disks, where n is the number of disks to be moved from tower A to tower c t Problem Analysis – Solution is a printed list of each disk move. Recursive function that can be used to move any number of disks from one tower to the other tower. 33

Towers of Hanoi t Program Design – If n is 1 • move disk 1 from. Tower to to. Tower – else • move n-1 disks from. Tower to aux tower using the to. Tower • move disk n from the from. Tower to the to. Tower • move n-1 disks from aux tower to the to. Tower using from. Tower 34

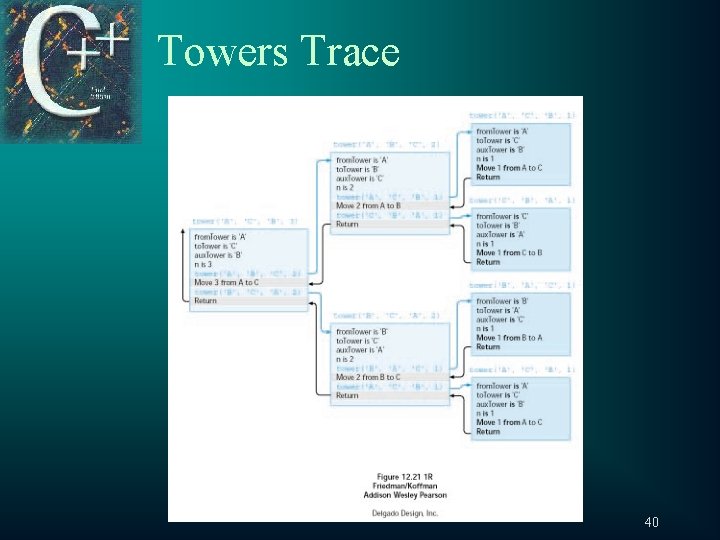
Towers of Hanoi t Program Implementation – Towers. cpp t Program Verification & Test – towers (‘A’, ’C’, ‘B’, 3); t Towers trace 35

Tower. cpp // File: tower. cpp // Recursive tower of hanoi function #include <iostream> using namespace std; void tower(char, int); int main() { int num. Disks; // input - number of disks 36

Tower. cpp cout << "How many disks: "; cin >> num. Disks; tower('A', 'C', 'B', num. Disks); return 0; } // // // Recursive function to "move" n disks from. Tower to to. Tower using aux. Tower Pre: The from. Tower, to. Tower, aux. Tower, and n are defined. Post: Displays the required moves. 37

Tower. cpp void tower (char from. Tower, char to. Tower, char aux. Tower, int n) { if (n == 1) cout << "Move disk 1 from tower " << from. Tower << " to tower " << to. Tower << endl; else { 38

Tower. cpp tower(from. Tower, aux. Tower, to. Tower, n-1); cout << "Move disk " << n << " from tower "<< from. Tower << " to tower " << to. Tower << endl; tower(aux. Tower, to. Tower, from. Tower, n-1); } } // end tower 39

Towers Trace 40

Tower. Test. cpp Program Output Move disk 1 from tower A to tower C Move disk 2 from tower A to tower B Move disk 1 from tower C to tower B Move disk 3 from tower A to tower C Move disk 1 from tower B to tower A Move disk 2 from tower B to tower C Move disk 1 from tower A to tower C 41

12. 6 Common Programming Errors t t t Stopping conditions Missing return statements Optimizations – recursion of arrays use large amounts of memory – use care when tracing your solutions 42