Recursion Chapter 10 Chapter Contents What Is Recursion

Recursion Chapter 10

Chapter Contents What Is Recursion? Tracing a Recursive Methods That Return a Value Recursively Processing an Array Recursively Processing a Linked Chain The Time Efficiency of Recursive Methods Time Efficiency of count. Down A Simple Solution to a Difficult Problem A Poor Solution to a Simple Problem

What Is Recursion? It is a problem-solving process involves repetition Breaks a problem into identical but smaller problems Eventually you reach a smallest problem Answer is obvious or trivial Using the solution to smallest problem enables you to solve the previous smaller problems Eventually the original big problem is solved An alternative to iteration An iterative solution involves loops

What Is Recursion? New Year Eve: counting down from 10.

What Is Recursion? A method that calls itself is a recursive method /** Task: Counts down from a given positive integer. * @param integer an integer > 0 */ public static void count. Down(int integer) { System. out. println(integer); if (integer > 1) count. Down(integer - 1); } // end count. Down Base case: a known case in a recursive definition. The smallest problem Eventually, one of the smaller problems must be the base case

When Designing Recursive Solution Four questions to ask before construct recursive solutions. If you follow these guidelines, you can be assured that it will work. How can you define the problem in terms of a smaller problem of the same type? How does each recursive call diminish the size of the problem? What instance of the problem can serve as the base case? As the problem size diminishes, will you reach this base case?

When Designing Recursive Solution For the method count. Down, we have the following answers. count. Down displays the given integer as the part of the solution that it contribute directly. Then call count. Down with smaller size. The smaller problem is counting down from integer -1. The if statement asks if the process has reached the base case. Here, the base case occurs when integer is 1.

Recursive Solution Guidelines Method definition must provide parameter Leads to different cases Typically includes an if or a switch statement One or more of these cases should provide a non recursive solution( infinite recursion if don’t) The base or stopping case One or more cases includes recursive invocation Takes a step towards the base case

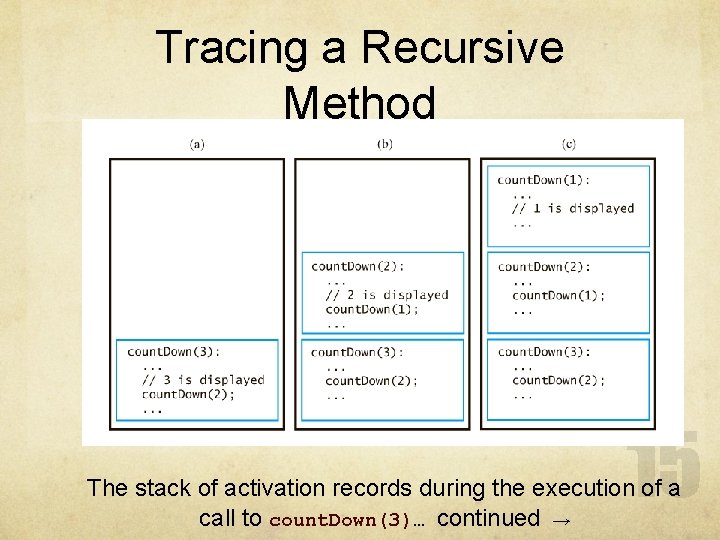
Tracing a Recursive Method Given: public static void count. Down(int integer) { System. out. println(integer); if (integer > 1) count. Down(integer - 1); } // end count. Down The effect of method call count. Down(3)

Tracing a Recursive Method Tracing the recursive call count. Down(3)

Compare Iterative and Recursive Programs //Recursive version public static void count. Down( integer) { if ( integer >= 1) { System. out. println(integer); count. Down(integer -1); } } //Iterative version public static void count. Down( integer) { while ( integer >= 1) { System. out. println(integer); integer--; } }

Question? Could you write an recursive method that skips n lines of output, where n is a positive integer. Use System. out. println() to skip one line. Describe a recursive algorithm that draws a given number of concentric circles. The innermost or outmost circle should have a given diameter. The diameter of each of the other circles should be three-fourths the diameter of the circle just outside it.

Answer to skip. Lines pubic static void skip. Lines ( int given. Number) { if (given. Number >=1) { System. out. println(); skip. Lines(given. Number – 1); } } void draw. Concentric. Circle( given. Number, given. Diameter) { // what should be put inside? ? ……. }

Tracing a Recursive Method Each call to a method generate an activation record that captures the state of the method’s execution and that is placed into a ADT stack. The activation-record stack remembers the history of incompleted method calls. A snapshot of a method’s state. The topmost activation record holds the data values for the currently executing method. When topmost method finishes, its activation record is popped In this way, Java can suspend the execution of a recursive method and re-

Tracing a Recursive Method The stack of activation records during the execution of a call to count. Down(3)… continued →

Tracing a Recursive Method Note: the recursive method will use more memory than an iterative method due to the stack of activation records ctd. The stack of activation records during the execution of a call to count. Down(3)

Tracing a Recursive Method Too many recursive calls can cause the error message “stack overflow”. Stack of activation records has become full. Method has used too much memory. Infinite recursion or large-size problems are the likely cause of this error.

Recursive Methods That Return a Value Task: Compute the sum 1 + 2 + 3 + … + n for an integer n > 0 public static int sum. Of(int n) { int sum; if (n = = 1) sum = 1; // base case else sum = sum. Of(n - 1) + n; // recursive call return sum; } // end sum. Of

Recursive Methods That Return a Value The stack of activation records during the execution of a call to sum. Of(3)

Recursively Processing an Array When processing array recursively, divide it into two pieces Last element one piece, rest of array another First element one piece, rest of array another Divide array into two halves A recursive method part of an implementation of an ADT is often private Its necessary parameters make it unsuitable as an ADT operation

Recursively Processing a Linked Chain To write a method that processes a chain of linked nodes recursively Use a reference to the chain's first node as the method's parameter Then process the first node Followed by the rest of the chain public void display() { display. Chain(first. Node); System. out. println(); } // end display private void display. Chain(Node node. One) { if (node. One != null) { System. out. print(node. One. data + " "); display. Chain(node. One. next); } } // end display. Chain

Recursively Divide the Array in Half public static void display. Array( int array[], int first, int last) { if (first == last) System. out. print(array[first]); else { int mid = (first + last) /2; display. Array(array, first, mid); display. Array(array, mid+1, last); } }

A Simple Solution to a Difficult Problem The initial configuration of the Towers of Hanoi for three disks

A Simple Solution to a Difficult Problem Rules for the Towers of Hanoi game 1. Move one disk at a time. Each disk you move must be a topmost disk. 2. No disk may rest on top of a disk smaller than itself. 3. You can store disks on the second pole temporarily, as long as you observe the previous two rules.

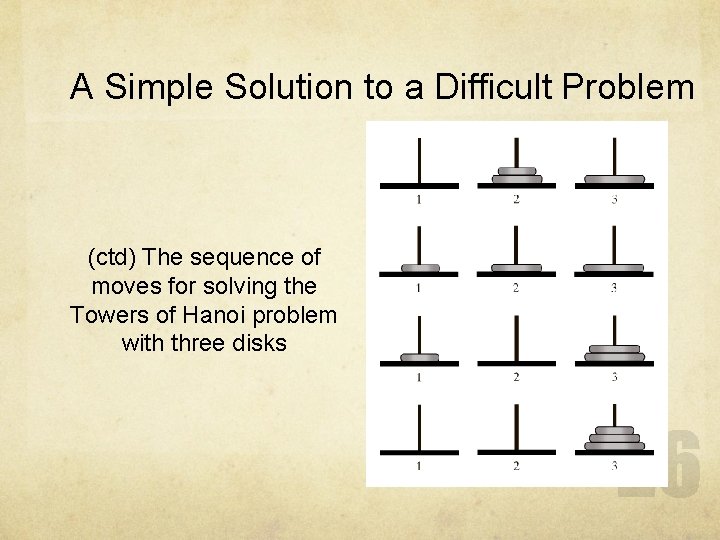
A Simple Solution to a Difficult Problem The sequence of moves for solving the Towers of Hanoi problem with three disks. Continued →

A Simple Solution to a Difficult Problem (ctd) The sequence of moves for solving the Towers of Hanoi problem with three disks

A Simple Solution to a Difficult Problem The smaller problems in a recursive solution for four disks

A Simple Solution to a Difficult Problem Algorithm for solution with 1 disk as the base case Algorithm solve. Towers(number. Of. Disks, start. Pole, temp. Pole, end. Pole) if (number. Of. Disks == 1) Move disk from start. Pole to end. Pole else { solve. Towers(number. Of. Disks-1, start. Pole, end. Pole, temp. Pole) Move disk from start. Pole to end. Pole solve. Towers(number. Of. Disks-1, temp. Pole, start. Pole, end. Pole) }

Recursion Efficiency How many moves occur for n disks? m(1) = 1 for n>1, two recursive calls to solve problems that have n-1 disks. m(n) = m(n-1) +1 = 2*m(n-1) +1 Let’s evaluate the recurrence for m(n) for a few values of n: m(1) =1; m(2) = 3; m(3) = 7; m(4) = 15; m(5) = 31; m(6) = 63…. m(n) = 2^n -1

Mathematical Induction Prove this conjecture m(n) = 2^n -1 by using mathematical induction: We know that m(1) =1, which equals to 2^1 -1=1, so the conjecture is true for n =1. Now assume that it is true for n=1, 2, …, k, and consider m(k+1) = 2*m(k) +1 (use the recurrence relation) =2*(2^k-1) +1 = 2^(k+1) -1 ( we assume that m(k) = 2^k-1) Since the conjecture is true for n=k+1, it is true for all n>=1

Mathematical Induction Assume you want to prove some statement P, P(n) is true for all n starting with n = 1. The Principle of Math Induction states that, to this end, one should accomplish just two steps: 1). Prove that P(1) is true. 2). Assume that P(k) is true for some k. Derive from here that P(k+1) is also true. look P(1) is true and implies P(2). Therefore P(2) is true. But P(2) implies P(3). Therefore P(3) is true which implies P(4) and so on.

Multiplying Rabbits (The Fibonacci Sequence) “Facts” about rabbits Rabbits never die A rabbit reaches sexual maturity exactly two months after birth, that is, at the beginning of its third month of life Rabbits are always born in male-female pairs At the beginning of every month, each sexually mature male-female pair gives birth to exactly one malefemale pair

Multiplying Rabbits (The Fibonacci Sequence) Problem How many pairs of rabbits are alive in month n? Month No calculation rabbit couples January 1 1+0=1 February 2 1+0=1 March 3 1+1=2 April 4 2+1=3 May 5 3+2=5 June 6 5+3=8 July 7 8 + 5 = 13 August 8 13 + 8 = 21 Recurrence relation rabbit(n) = rabbit(n-1) + rabbit(n-2)

A Poor Solution to a Simple Problem Fibonacci numbers First two numbers of sequence are 1 and 1 Successive numbers are the sum of the previous two 1, 1, 2, 3, 5, 8, 13, … This has a natural looking recursive solution Turns out to be a poor (inefficient) solution

A Poor Solution to a Simple Problem The recursive algorithm Algorithm Fibonacci(n) if (n <= 1) return 1 else return Fibonacci(n-1) + Fibonacci(n-2)

A Poor Solution to a Simple Problem Time efficiency grows exponentially with n, which is k^n Iterative solution is O(n) int fib(int n) { int f[n+1]; f[1] = f[2] = 1; for (int i = 3; i <= n; i++) f[i] = f[i-1] + f[i-2]; return f[n]; } The computation of the Fibonacci number F 6 (a) recursively; (b) iteratively