Recurrence Relations Selected Exercises Exercise 10 a A

Exercise 10 (a) A person deposits $1, 000 in an account that yields 9%

Exercise 10 (a) Solution A person deposits $1, 000 in an account that yields

Exercise 10 (b) A person deposits $1, 000 in an account that yields 9%

Exercise 10 (b) Solution After 1 year, a 1 = 1. 09 a 0

Exercise 10 (b) Solution Basis n = 0: a 0 = 1000 x(1. 09)0.

Exercise 10 (c) A person deposits $1, 000 in an account that yields 9%

Exercise 10 (c) Solution The account contains a 100 dollars after 100 years: a

Exercise 20 A country uses as currency coins with pesos values of 1, 2,

Exercise 20 Solution The sequences that start w/ a 1 peso coin differ from

Exercise 30 (a) A string that contains only 0 s, 1 s, & 2

Exercise 30 (a) Solution Subtract the # of “bad” strings (contain 2 consecutive 0

Exercise 30 (b) What are the initial conditions? Copyright © Peter Cappello 13

Exercise 30 (b) Solution What are the initial conditions? b 0 = b 1

Exercise 30 (c) How many ternary strings of length 6 contain 2 consecutive 0

Exercise 30 (c) Solution The number of such strings is the value of b

Exercise 40 Find a recurrence relation, en, for the # of bit strings of

Exercise 40 Solution Strings are sequences: Order matters: There is a 1 st bit.

Use the Binomial Theorem ( x + y )n = Σj=0 to n C(

49 The variation we consider begins with people numbered 1, …, n, standing around

49 Solution Put 5 people, named 1, 2, 3, 4, & 5, in a

50 Use the values you found in Exercise 49 to conjecture a formula for

50 Solution continued n 1 = 20 + 0 2 = 21 + 0

50 Solution continued So, if n = 2 m + k, where m, k

Exercise 20 Solution continued But, we also can use bills. If the 1 st

Slides: 29

Download presentation

Recurrence Relations: Selected Exercises

Exercise 10 (a) A person deposits $1, 000 in an account that yields 9% interest compounded annually. Set up a recurrence relation for the amount in the account at the end of n years. Copyright © Peter Cappello 2

Exercise 10 (a) Solution A person deposits $1, 000 in an account that yields 9% interest compounded annually. Set up a recurrence relation for the amount in the account at the end of n years. Let an represent the amount after n years. an = an-1 + 0. 09 an-1 = 1. 09 an-1 a 0 = 1000. Copyright © Peter Cappello 3

Exercise 10 (b) A person deposits $1, 000 in an account that yields 9% interest compounded annually. Find an explicit formula for the amount in the account at the end of n years. Copyright © Peter Cappello 4

Exercise 10 (b) Solution After 1 year, a 1 = 1. 09 a 0 = 1. 09 x 1000 = 1000 x 1. 091 After 2 years, a 2 = 1. 09 a 1 = 1. 09( 1000 x(1. 09)1 ) = 1000 x(1. 09)2 After n years, an = 1000 x(1. 09)n Since an is recursively defined, we prove the formula, for n ≥ 0, by mathematical induction (The problem does not ask for proof). Copyright © Peter Cappello 5

Exercise 10 (b) Solution Basis n = 0: a 0 = 1000 x(1. 09)0. The 1 st equality is the recurrence relation’s initial condition. Induction hypothesis: an = 1000 x 1. 09 n. Induction step: Show: an+1 = 1000 x 1. 09 n+1. an+1 = 1. 09 an = 1. 09 ( 1000 x 1. 09 n ) = 1000 x 1. 09 n+1. The 1 st equality: the definition of the recurrence relation. The 2 nd equality: the induction hypothesis. Copyright © Peter Cappello 6

Exercise 10 (c) Solution The account contains a 100 dollars after 100 years: a 100 = 1000 x 1. 09100 = $5, 529, 041. That is before taxes. With 30% federal + 10% CA on interest earned, it becomes 1000 x 1. 05100 = $131, 500 Copyright © Peter Cappello 8

Exercise 20 A country uses as currency coins with pesos values of 1, 2, 5, & 10 pesos Find a recurrence relation, an, for the # of payment sequences for n pesos. E. g. , a bill of 4 pesos could be paid with any of the following sequences: 1. 1, 1, 1, 1 2. 1, 1, 2 3. 1, 2, 1 4. 2, 1, 1 5. 2, 2 Copyright © Peter Cappello 9

Exercise 20 Solution The sequences that start w/ a 1 peso coin differ from the sequences that don’t. Use the sum rule: Partition the set of sequences, based on which kind of coin starts the sequence. It could be a: • 1 peso coin, in which case we have an-1 ways to finish the bill • 2 peso coin, in which case we have an-2 ways to finish the bill • 5 peso coin, in which case we have an-5 ways to finish the bill • 10 peso coin, in which case we have an-10 ways to finish the bill The recurrence relation is an = an-1 + an-2 + an-5 + an-10 with 10 initial conditions, a 1 = 1, a 2 = 2, a 3 = 3, a 4 = 5, a 5 = 9, a 6 = 15, a 7 = 26, a 8 = 44, a 9 = 75, a 10 = 125. Copyright © Peter Cappello 10

Exercise 30 (a) A string that contains only 0 s, 1 s, & 2 s is called a ternary string. Find a recurrence relation for the # of ternary strings of length n that do not contain 2 consecutive 0 s. Copyright © Peter Cappello 11

Exercise 30 (a) Solution Subtract the # of “bad” strings (contain 2 consecutive 0 s), bn, , from the # of ternary strings, 3 n. To count bn, , use the sum rule: Partition the set of strings, depending on what digit starts the string: • The string starts with a 1: bn-1 ways to finish the string. • The string starts with a 2: bn-1 ways to finish the string. • The string starts with a 0: – The remaining string starts with a 0: 3 n-2 ways to finish the string. – The remaining string starts with a 1: bn-2 ways to finish the string. – The remaining string starts with a 2: bn-2 ways to finish the string. Summing, bn = 2 bn-1 + 2 bn-2 + 3 n-2 Copyright © Peter Cappello 12

Exercise 30 (c) Solution The number of such strings is the value of b 6. Using bn = 2 bn-1 + 2 bn-2 + 3 n-2, we compute: b 0 = b 1 = 0. (Initial conditions) b 2 = 2 b 1 + 2 b 0 + 30 = 2 x 0 + 30 = 1 b 3 = 2 b 2 + 2 b 1 + 31 = 2 x 1 + 2 x 0 + 31 = 5 b 4 = 2 b 3 + 2 b 2 + 32 = 2 x 5 + 2 x 1 + 32 = 21 b 5 = 2 b 4 + 2 b 3 + 33 = 2 x 21 + 2 x 5 + 33 = 79 b 6 = 2 b 5 + 2 b 4 + 34 = 2 x 79 + 2 x 21 + 34 = 281. Copyright © Peter Cappello 16

Exercise 40 Solution Strings are sequences: Order matters: There is a 1 st bit. Use the sum rule: Partition the desired set of bit strings, based on the string’s 1 st bit: Strings with an even # of 0 s that begin with 1: en-1 Strings with an even # of 0 s that begin with 0: 2 n-1 - en-1 Summing, en = en-1 + 2 n-1 - en-1 = 2 n-1 Copyright © Peter Cappello 18

Use the Binomial Theorem ( x + y )n = Σj=0 to n C( n, j )xn-jyj = C( n, 0 )xny 0 + C( n, 1 )xn-1 y 1 + … + C( n, j )xn-jyj + … + C( n, n )x 0 yn. Evaluate at x = 1, y = -1: (1 – 1)n = Σj=0 to n C( n, j )1 n-j( -1 )j = C( n, 0 ) - C( n, 1 ) + C( n, 2 ) - C( n, 3 ) +-. . . (-1)n. C( n, n ). C( n, 1 ) + C( n, 3 ) + C( n, 5 ). . . = C( n, 0 ) + C( n, 2 ) + C( n, 4 ). . . = 2 n-1 Example: C(4, 0) + C(4, 2) + C(4, 4) = C(4, 1) + C(4, 3) = 23 The # of bit strings of length 4 that have an even number of 0 s is 23. Copyright © Peter Cappello 21

49 The variation we consider begins with people numbered 1, …, n, standing around a circle. In each stage, every 2 nd person still alive is killed until only 1 survives. We denote the number of the survivor by J(n). Determine the value of J(n) for 1 n 16. Copyright © Peter Cappello 2011 22

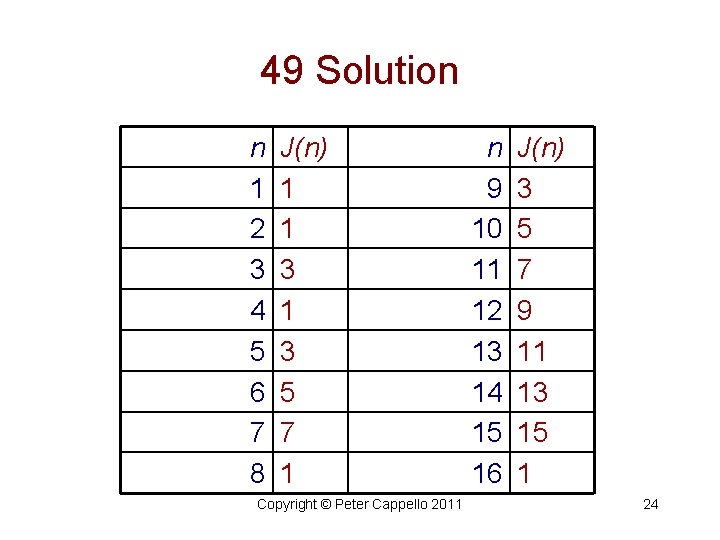
49 Solution Put 5 people, named 1, 2, 3, 4, & 5, in a circle. Starting with 1, kill every 2 nd person until only 1 person is left. The sequence of killings is: 12345 12345 So, J(5) = 3. Continuing, for each value of n, results in the following table. Copyright © Peter Cappello 2011 23

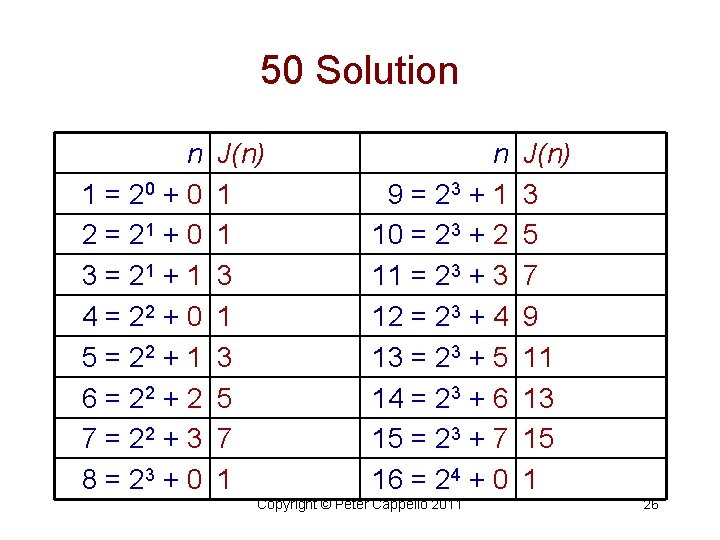
50 Solution n 1 = 20 + 0 2 = 21 + 0 3 = 21 + 1 4 = 22 + 0 5 = 22 + 1 6 = 22 + 2 7 = 22 + 3 8 = 23 + 0 J(n) 1 1 3 5 7 1 n 9 = 23 + 1 10 = 23 + 2 11 = 23 + 3 12 = 23 + 4 13 = 23 + 5 14 = 23 + 6 15 = 23 + 7 16 = 24 + 0 Copyright © Peter Cappello 2011 J(n) 3 5 7 9 11 13 15 1 26

50 Solution continued n 1 = 20 + 0 2 = 21 + 0 3 = 21 + 1 4 = 22 + 0 5 = 22 + 1 6 = 22 + 2 7 = 22 + 3 8 = 23 + 0 J(n) 1 = 2*0 + 1 3 = 2*1 + 1 5 = 2*2 + 1 7 = 2*3 + 1 1 = 2*0 + 1 n 9 = 23 + 1 10 = 23 + 2 11 = 23 + 3 12 = 23 + 4 13 = 23 + 5 14 = 23 + 6 15 = 23 + 7 16 = 24 + 0 Copyright © Peter Cappello 2011 J(n) 3 = 2*1 + 1 5 = 2*2 + 1 7 = 2*3 + 1 9 = 2*4 + 1 11 = 2*5 + 1 13 = 2*6 + 1 15 = 2*7 + 1 1 = 2*0 + 1 27

Exercise 20 Solution continued But, we also can use bills. If the 1 st currency object is a bill, it could be a 1. 5 peso, in which case we have an-5 ways to finish the bill 2. 10 peso, in which case we have an-10 ways to finish the bill 3. 20 peso, in which case we have an-20 ways to finish the bill 4. 50 peso, in which case we have an-50 ways to finish the bill 5. 100 peso, in which case we have an-100 ways to finish the bill Using both coins & bills, we have an = an-1 + an-2 + an-5 + an-10 + an-20 + an-50 + an-100 = an-1 + an-2 + 2 an-5 + 2 an-10 + an-20 + an-50 + an-100 , with 100 initial conditions, which I will not produce. Copyright © Peter Cappello 29