Recurrence Relations Connection to recursive algorithms Techniques for

Recurrence Relations • Connection to recursive algorithms • Techniques for solving them

Recursion and Mathematical Induction In both, we have general and boundary conditions: The general conditions break the problem into smaller and smaller pieces. The initial or boundary condition(s) terminate the recursion. Both take a Divide and Conquer approach to solving mathematical problems.

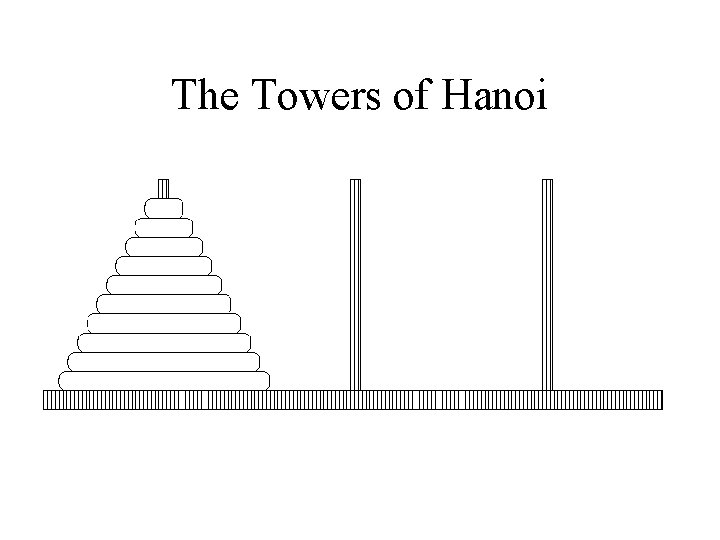
The Towers of Hanoi

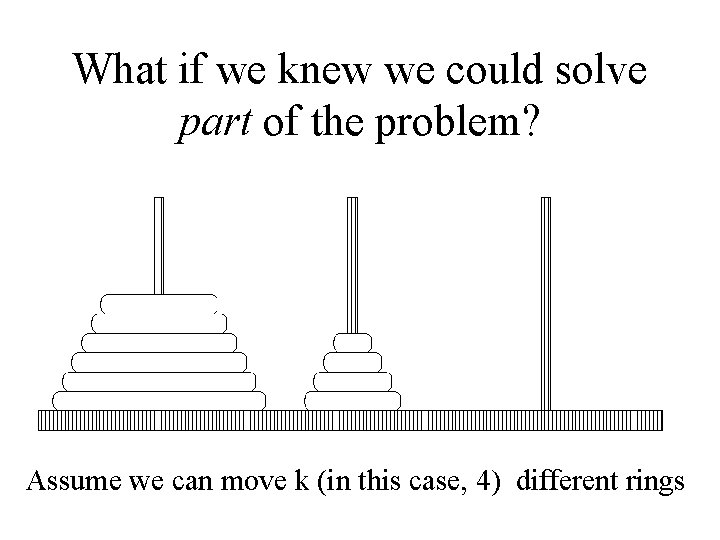
What if we knew we could solve part of the problem? Assume we can move k (in this case, 4) different rings

Can we do one better?

Solved for one more!

Where do recurrence relations come from? • Analysis of a divide and conquer algorithm – Towers of Hanoi, Merge Sort, Binary Search • Analysis of a combinatorial object – up-down permutations • This is the key analysis step I want you to master • Use small cases to check correctness of your recurrence relation

Can recurrence relations be solved? • No general procedure for solving recurrence relations is known, which is why it is an art. • However, linear, finite history, constant coefficient recurrences always can be solved • Example: an = 2 an-1 + 2 an-2 +1 ; a 1 = 1 ; a 2 = 1 – degree = 1 – history = 2 – coefficients = 2, 2, and 1 • In the end, what is the best way to solve this? – Software like Mathematica or Maple, but I still want you to be able to solve some on your own without such aid

Solution Techniques • Guess a solution and prove by induction. – Try back-substituting until you know what is going on. – Draw a recursion tree. • Master Theorem • General Technique

First step • Using the base case and the recursive case, calculate small values • Use these values to help guess a solution • Use these values to help verify correctness of your closed form solution

Guessing solution and proving by induction We can use mathematical induction to prove that a general function solves for a recursive one. Tn = 2 Tn-1 + 1 ; T 0 = 0 n = 0 1 2 3 Tn = Guess what the solution is? 4 5 6 7 8

Guessing solution and proving by induction II Prove: Tn = 2 n - 1 by induction: 1. Base Case: n=0: T 0 = 20 - 1 = 0 2. Now assume Tn = 2 n – 1 for n ≥ 0 3. Inductive Step: Show Tn+1 = 2 n+1 – 1 for n ≥ 0 Tn+1 = 2 Tn + 1 = 2 ( 2 n - 1 ) + 1 = 2 n+1 -1

Back-substitution Example: T(n) = 3 T( n/4 ) + n, T(1) = 1 = 3(3 T( n/16 )+n/4) + n = 9 T( n/16 ) + 3 n/4 + n = 9(3 T( n/64 ) +n/16) + 3 n/4 + n = 27 T( n/64 )+9 n/16 + 3 n/4 + n

Recursion Trees T(n) = 2 T(n/2) + n 2 , T(1) = 1

Example Problem Use induction to prove that Merge. Sort is an O(n log n) algorithm. Mergesort(array) n = size(array) if ( n == 1) return array 1 = Mergesort(array[1. . n/2]) array 2 = Mergesort(array[n/2. . n]) return Merge(array 1, array 2)

Induction Proof Example: Prove that T(n) = 2 T( n/2 ) + n , T(1) = 1 is O(n log n). We need to prove that T(n) ≤ c n log n , for all n greater than some value. Base cases: T(2) = 4 ≤ c 2 and T(3) = 5 ≤ c 3 log 2 3 c ≥ 2 suffices Inductive step: Assume T( n/2 ) ≤ c ( n/2 ) log ( n/2 ) Question: Quantification on n for above assumption? Show that T(n) ≤ c n log n.

Induction Step Given : T( n/2 ) ≤ c ( n/2 ) log ( n/2 ) T(n) = 2 T( n/2 ) + n ≤ 2( c( n/2 ) log ( n/2 ) ) + n ≤ 2( c(n/2) log (n/2) ) + n (dropping floors makes it bigger!) = c n log(n/2) + n = c n ( log(n) - log(2) ) + n = c n log(n) - c n + n (log 22 = 1) = c n log(n) - (c - 1) n < c n log(n) (c > 1 )

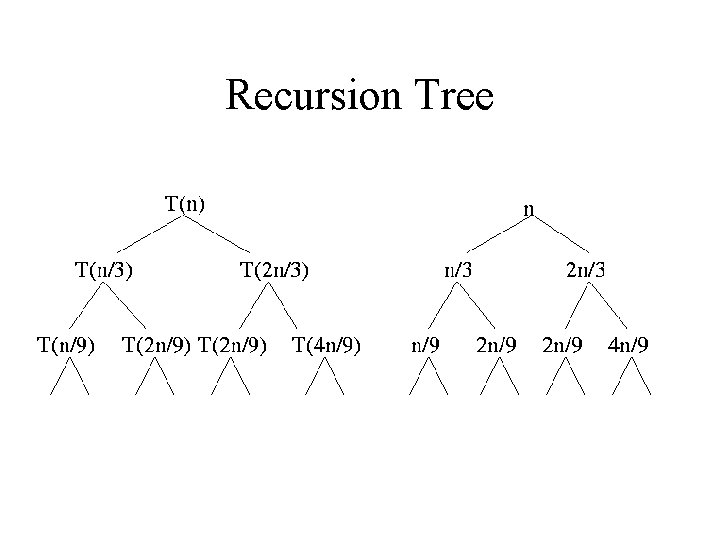
Example Problem 2 T(n) = T(n/3) + T(2 n/3) + n T(1) = 1 Show T(n) is (n log n) by appealing to the recursion tree.

Recursion Tree

Master Theorem • T(n) = a T(n/b) + f(n) – Ignore floors and ceilings for n/b – constants a ≥ 1 and b > 1 – f(n) any function • If f(n) = O(nlog_b a-e) for constant e>0, T(n) = Q(nlog_b a) • If f(n) = Q(nlog_b a), T(n) = Q(nlog_b a lg n) • If f(n) = (nlog_b a+e) for some constant e >0, and if af(n/b) ≤ c f(n) for some constant c < 1 and all sufficiently large n, T(n) = Q(f(n)). • Key idea: Compare nlog_b a with f(n)

Examples Revisited • Tn = 2 Tn-1 + 1 ; T 0 = 0 • Example: T(n) = 3 T( n/4 ) + n, T(1) = 1 • Example: Prove that T(n) = 2 T( n/2 ) + n , T(1) = 1 is O(n log n). • T(n) = T(n/3) + T(2 n/3) + n

Characteristic Equation Approach • tn = 3 tn-1 + 4 tn-2 for n > 1 – t 0 = 0, t 1 = 5 • Rewrite recurrence – tn - 3 tn-1 - 4 tn-2 = 0 • Properties – Homogeneous: no terms not involving tn – Linear: tn terms have no squares or worse – constant coefficients: 1, -3, -4

Characteristic Equation • tn - 3 tn-1 - 4 tn-2 = 0 • Rewrite assuming solution of the form tn = xn • xn – 3 xn-1 – 4 xn-2 = 0 • xn-2 (x 2 – 3 x – 4) = 0 • Find roots of (x 2 – 3 x – 4) – (x+1)(x-4) roots are -1 and 4 • Solution is of form c 1(-1)n + c 24 n

Solving for constants • tn = c 1(-1)n + c 24 n • Use base cases to solve for constants – t 0 = c 1(-1)0 + c 240 = c 1 + c 2 – t 1 = 5 = c 1(-1)1 + c 241 = -c 1 + 4 c 2 – 5 c 2 = 5 c 2 = 1 c 1 = -1 • tn = (-1)n+1 + 4 n • Always test solution on small values!

Repeated roots for char. eqn • tn - 5 tn-1 + 8 tn-2 – 4 tn-3= 0 – boundary conditions: tn = n for n = 0, 1, 2 • x 3 - 5 x 2 + 8 x – 4 = 0 • (x-1)(x-2)2 roots are 1, 2, 2 • Solution is of form c 1(1)n + c 22 n + c 3 n 2 n – If root is repeated third time, then n 22 n term, and so on

Solving for constants • tn = c 1(1)n + c 22 n + c 3 n 2 n • Use base cases to solve for constants – – t 0 = c 1(1)0 + c 220 + c 30 20 = c 1 + c 2 t 1 = c 1(1)1 + c 221 + c 31 21 = c 1 + 2 c 2 + 2 c 3 t 2 = c 1(1)2 + c 222 + c 32 22 = c 1 + 4 c 2 + 8 c 3 c 1 = -2, c 2 = 2, c 3 = -1/2 • tn = 2 n+1 – n 2 n-1 – 2 • Test the solution on small values!

Inhomogeneous Equation • tn - 2 tn-1 = 3 n – base case value for t 0 only • (x – 2) (x-3) = 0 – (x-2) term comes from homogeneous solution – If rhs is of form bn poly(n) of degree d • In this case, b = 3, poly (n) = 1 is of degree 0 – Plug (x-b)d+1 into characteristic equation

Solving for constants • • • (x – 2) (x-3) = 0 tn = c 12 n + c 23 n Solve for c 1 and c 2 with only t 0 base case This is only 1 equation and 2 unknowns Use recurrence to generate extra equations – tn - 2 tn-1 = 3 n t 1 = 2 t 0 + 3 • Now we have two equations – t 0 = c 120 + c 230 = c 1 + c 2 – t 1 = 2 t 0 + 3 = c 121 + c 231 = 2 c 1 + 3 c 2 – c 1 = t 0 – 3 and c 2 = 3 • tn = (t 0 -3)2 n + 3 n+1

Changing variable • tn – 3 tn/2 = n if n is a power of 2 – t 1 = 1 • Let n = 2 i and si = tn • si – 3 si-1 = 2 i for i >= 1 – s 0 = 1 • (x-3)(x-2) = 0 – x-3 from characteristic equation – x-2 bnpoly(n) rhs

Solving for constants • (x-3)(x-2) = 0 • si = c 13 i + c 22 i • Generating two equations – t 1 = s 0 = 1 = c 130 + c 220 = c 1 + c 2 – t 2 = s 1 = 3 t 1+2 = 5 = c 131 + c 221 = 3 c 1 + 2 c 2 – c 1 = 3, c 2 = -2 • si = 3 i+1 – 2 i+1 for i >= 0 • tn = 3 nlg 3 – 2 n for n a power of 2 >= 1

Example: Up-down Permutations • An up-down permutation is a permutation of the numbers from 1 to n such that the numbers strictly increase to n and then decrease thereafter • Examples – 1376542, 7654321, 3476521 • Let tn denote the number of up-down permutations – What is recurrence relation for tn? – What is solution?

Example: Towers of Hanoi • Suppose we have two disks of each size. • Let n be the number of sizes of disks – What is recurrence relation? – What is solution?

Example: Merge Sort • Merge sort breaking array into 3 pieces – What is recurrence relation? – What is solution? – How does this compare to breaking into 2 pieces?