RECTANGLES Recognize and apply properties of rectangles Determine


- Slides: 14

RECTANGLES • Recognize and apply properties of rectangles. • Determine whether parallelograms are rectangles. Parts of the tennis court are marked by parallel and perpendicular lines.

PROPERTIES OF RECTANGLES A rectangle is a quadrilateral with four right angles. Since both pairs of opposite angles are congruent, it follows that a rectangle is a special type of parallelogram.

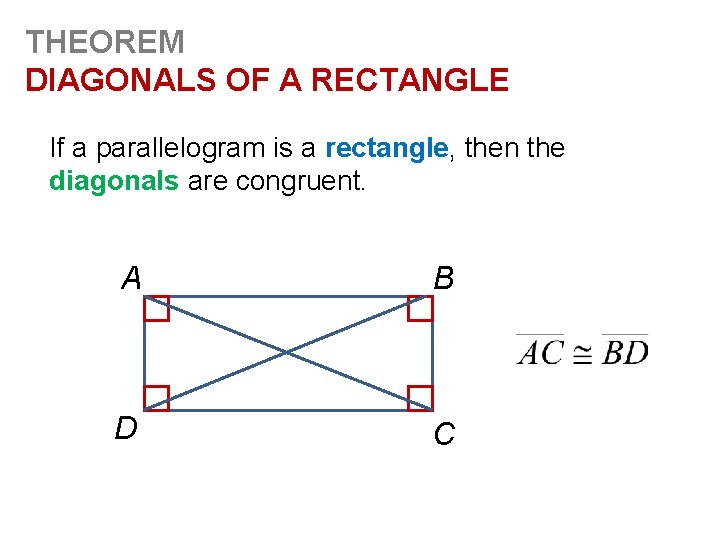
THEOREM DIAGONALS OF A RECTANGLE If a parallelogram is a rectangle, then the diagonals are congruent. A B D C

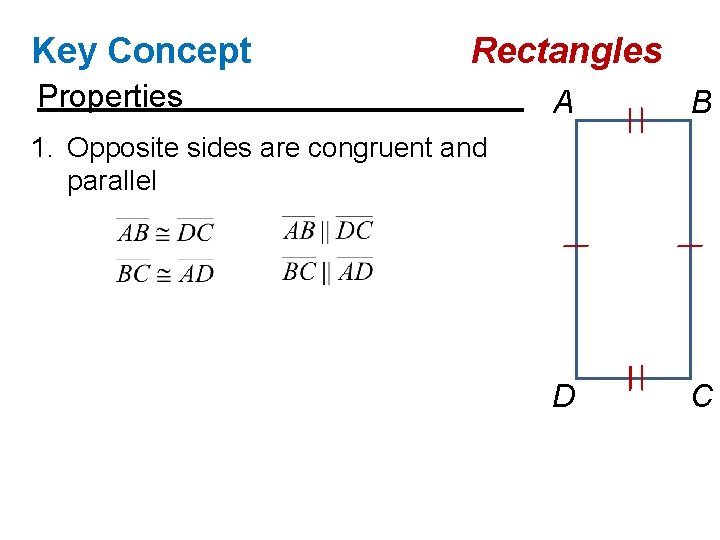
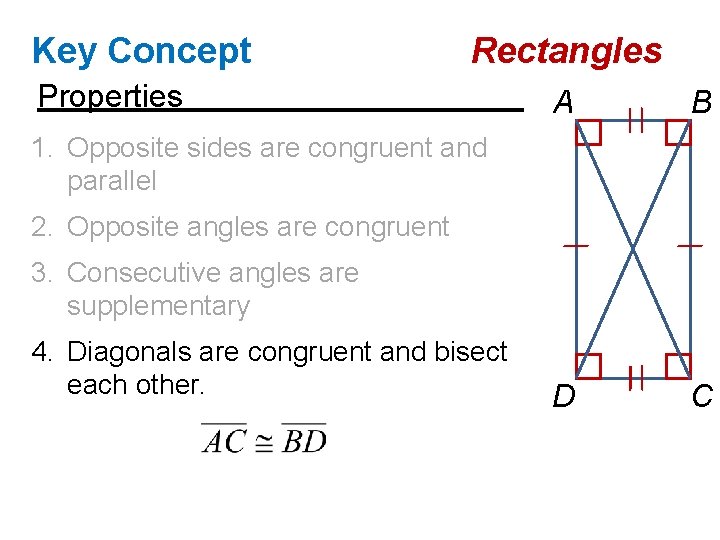
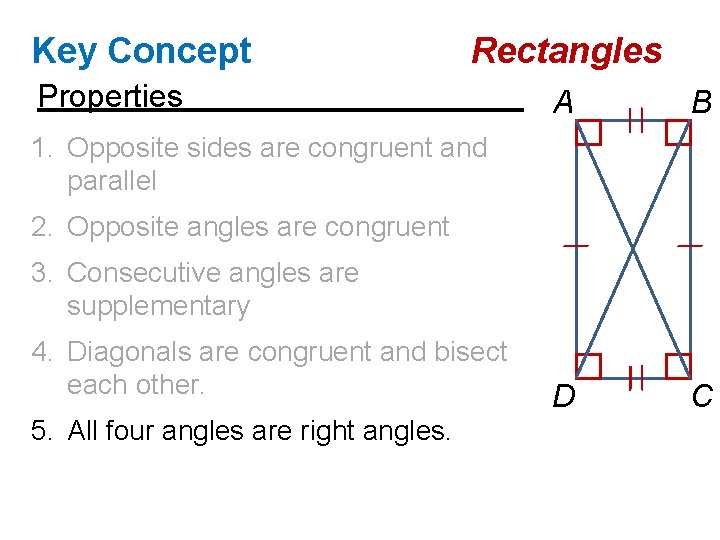
Key Concept Rectangles Properties A B D C 1. Opposite sides are congruent and parallel

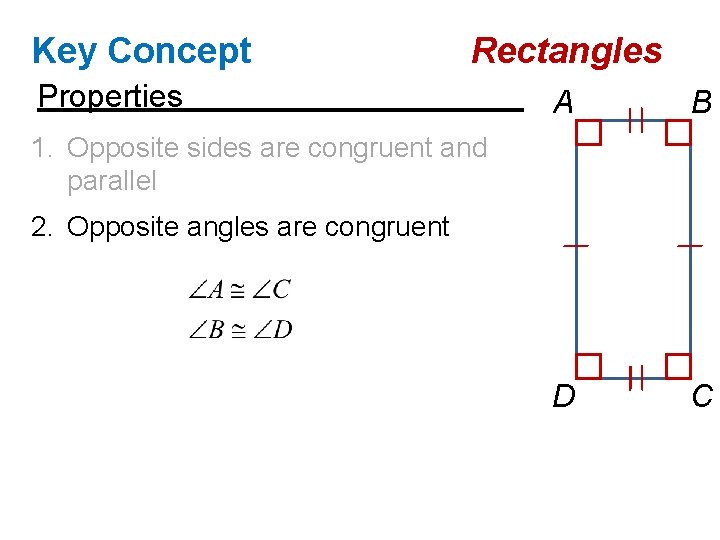
Key Concept Rectangles Properties A B D C 1. Opposite sides are congruent and parallel 2. Opposite angles are congruent

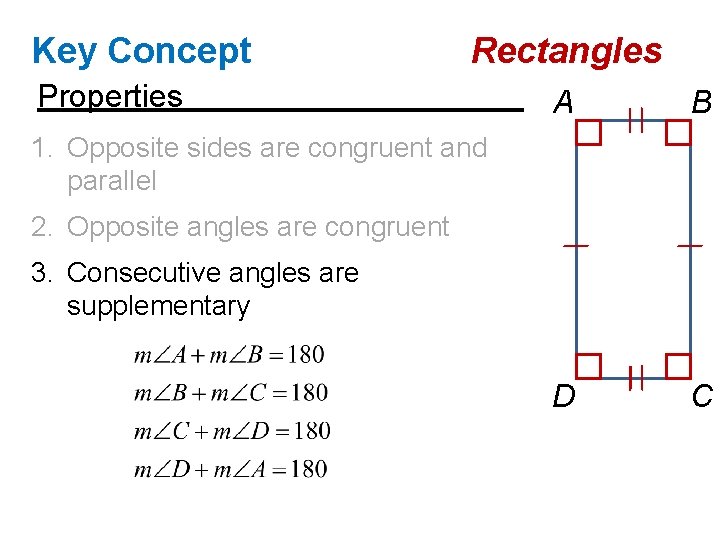
Key Concept Rectangles Properties A B D C 1. Opposite sides are congruent and parallel 2. Opposite angles are congruent 3. Consecutive angles are supplementary

Key Concept Rectangles Properties A B D C 1. Opposite sides are congruent and parallel 2. Opposite angles are congruent 3. Consecutive angles are supplementary 4. Diagonals are congruent and bisect each other.

Key Concept Rectangles Properties A B D C 1. Opposite sides are congruent and parallel 2. Opposite angles are congruent 3. Consecutive angles are supplementary 4. Diagonals are congruent and bisect each other. 5. All four angles are right angles.

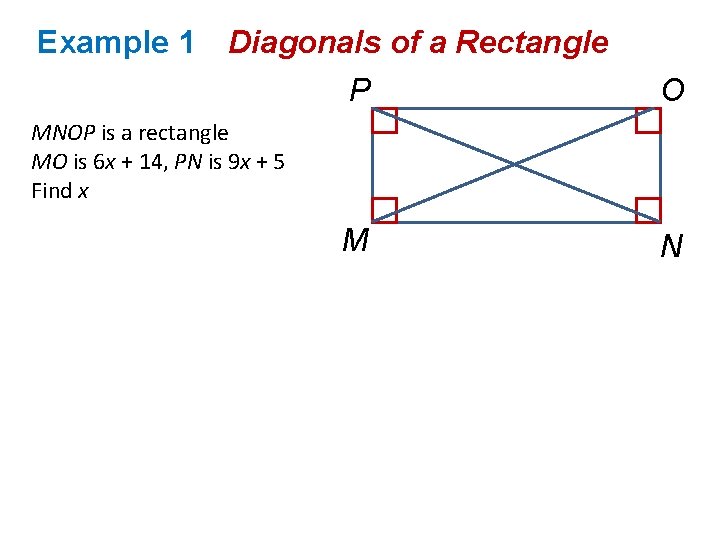
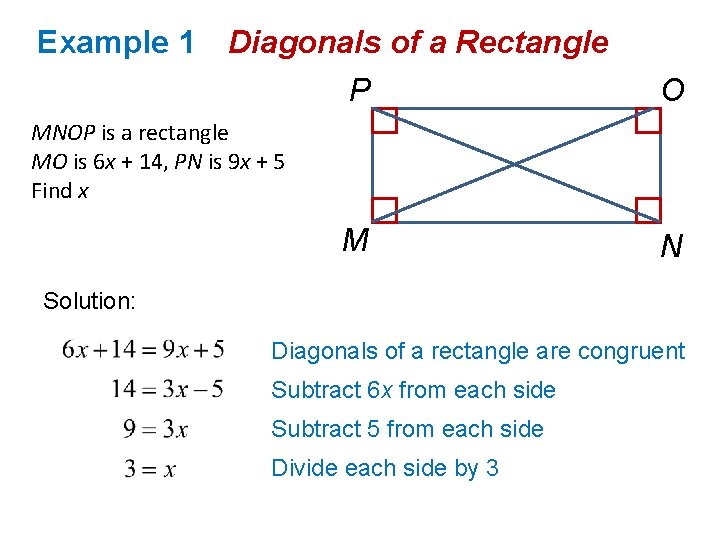
Example 1 Diagonals of a Rectangle P O MNOP is a rectangle MO is 6 x + 14, PN is 9 x + 5 Find x M N

Example 1 Diagonals of a Rectangle P O MNOP is a rectangle MO is 6 x + 14, PN is 9 x + 5 Find x M N Solution: Diagonals of a rectangle are congruent Subtract 6 x from each side Subtract 5 from each side Divide each side by 3

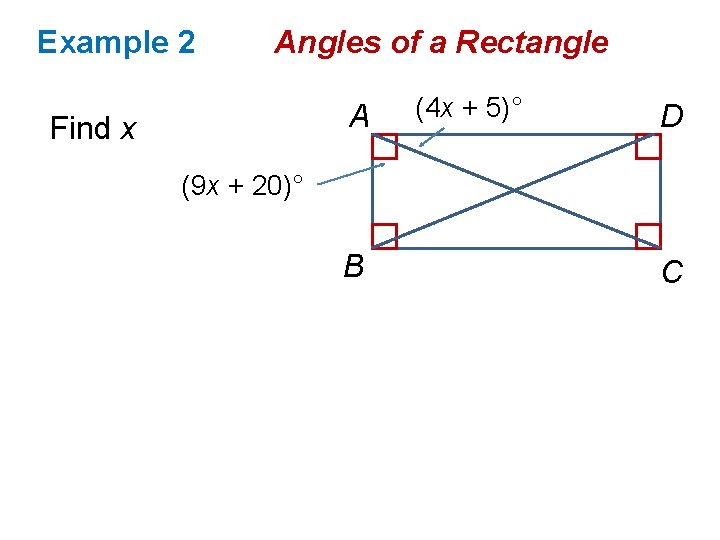
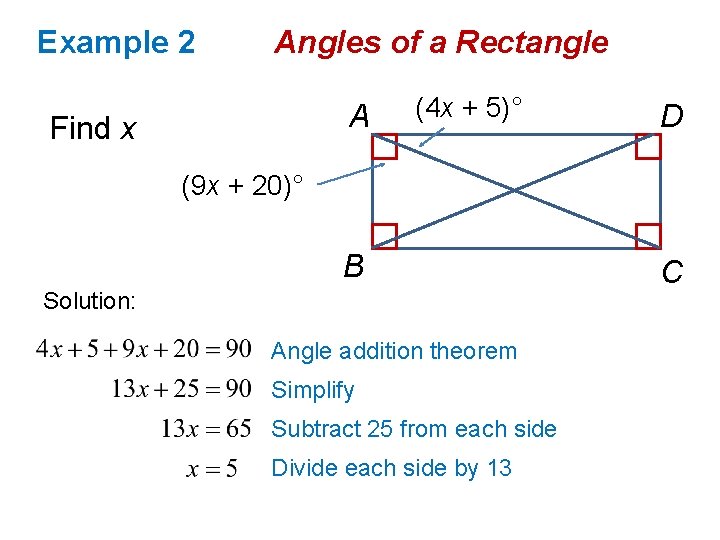
Example 2 Angles of a Rectangle A Find x (4 x + 5)° D (9 x + 20)° B C

Example 2 Angles of a Rectangle A Find x (4 x + 5)° D (9 x + 20)° B Solution: Angle addition theorem Simplify Subtract 25 from each side Divide each side by 13 C

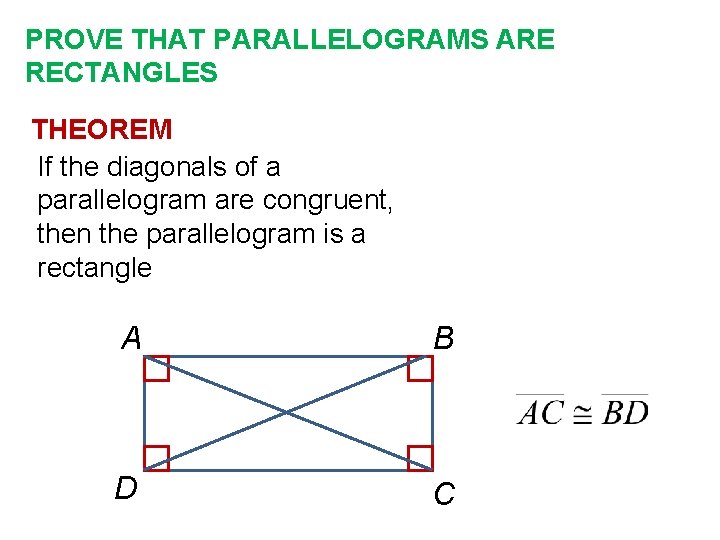
PROVE THAT PARALLELOGRAMS ARE RECTANGLES THEOREM If the diagonals of a parallelogram are congruent, then the parallelogram is a rectangle A B D C

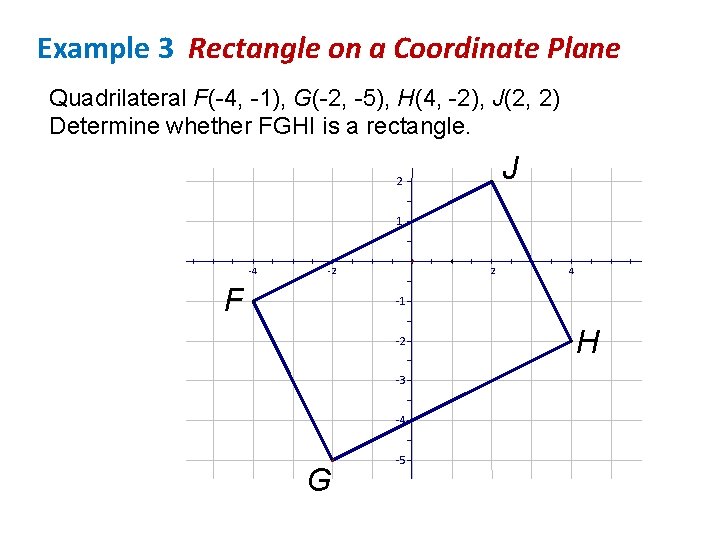
Example 3 Rectangle on a Coordinate Plane Quadrilateral F(-4, -1), G(-2, -5), H(4, -2), J(2, 2) Determine whether FGHI is a rectangle. J 2 1 -4 -2 F 2 4 -1 -2 -3 -4 G -5 H