Recordando Termodinmica I Bibliografia A Modern Course in

Recordando Termodinámica I

Bibliografia A Modern Course in Statistical Mechanics L. E. Reichl Statistical Mechanics K. Huang Statistical Mechanics R. K. Pathria Introduction to Modern Statistical Mechanics D. Chandler Introduction to Phase Transitions and critical Phenomena H. Eugene Stanley

precisión


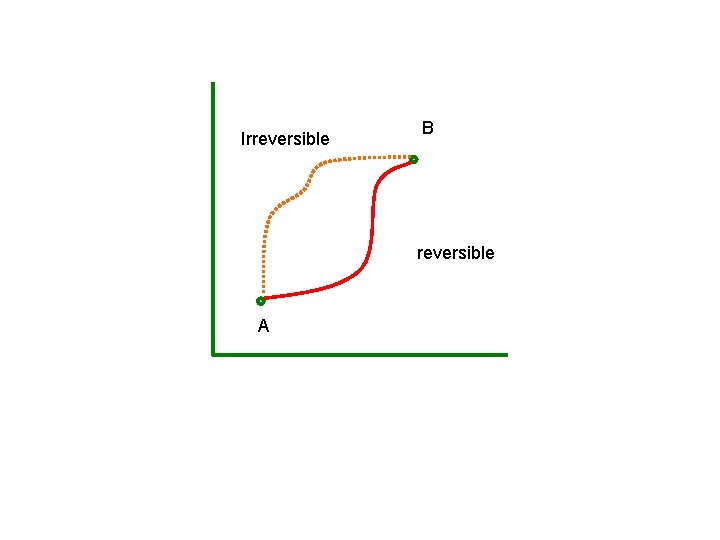
Irreversible B reversible A






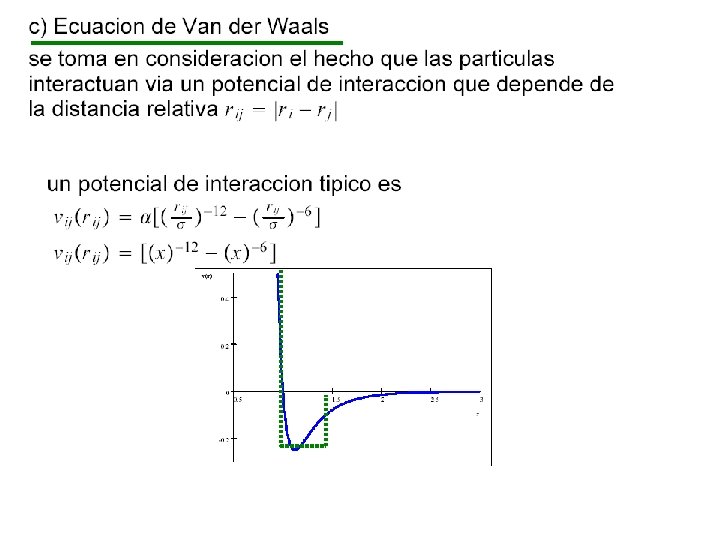

lala
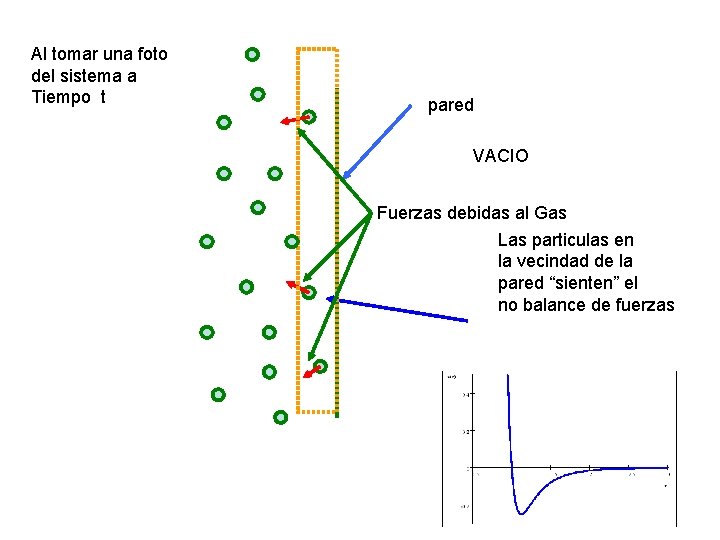
Al tomar una foto del sistema a Tiempo t pared VACIO Fuerzas debidas al Gas Las particulas en la vecindad de la pared “sienten” el no balance de fuerzas



A B
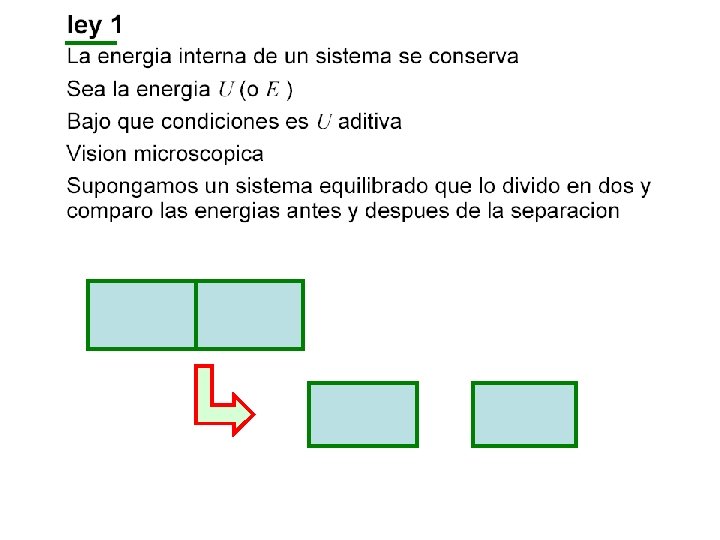
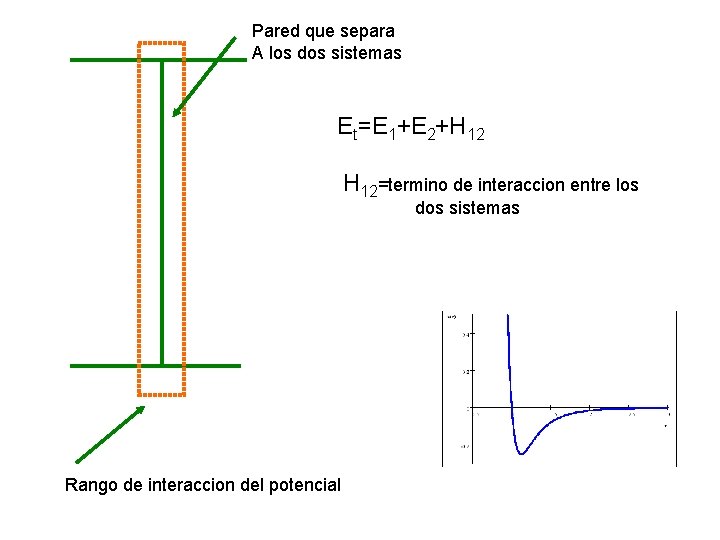
Pared que separa A los dos sistemas Et=E 1+E 2+H 12=termino de interaccion entre los dos sistemas Rango de interaccion del potencial
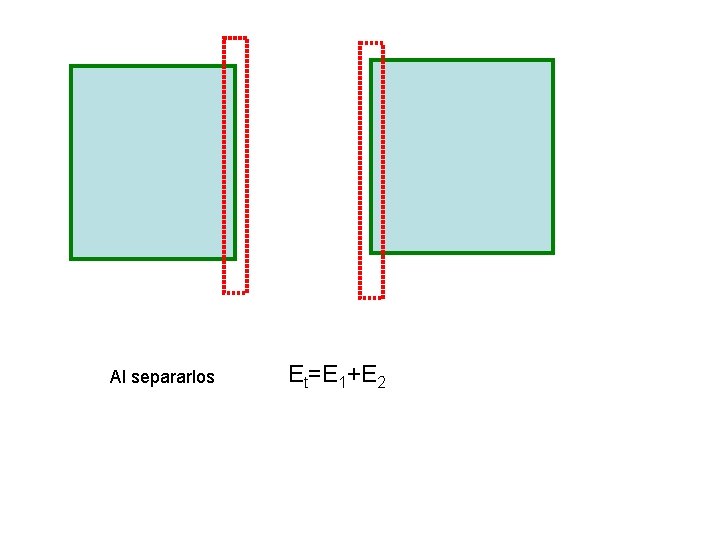
Al separarlos Et=E 1+E 2
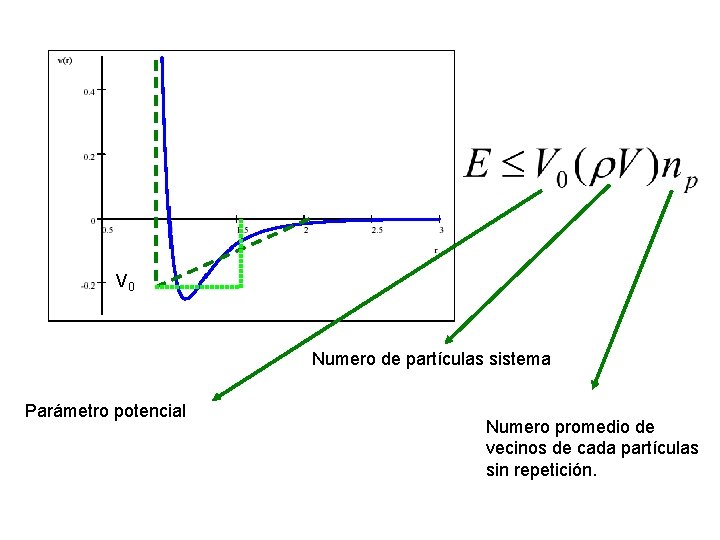
V 0 Numero de partículas sistema Parámetro potencial Numero promedio de vecinos de cada partículas sin repetición.

La energia de interaccion puede ser estimada como E~V 0* numero de particulas*numero de pares de una particula E~V 0* *V*np Esto vale para cada uno de los sistemas 1 y 2 E 1+E 2 ~ V 0* * (V 1+V 2)*np Para la interface H 12~V 0* *V’*np De donde H 12/(E 1+E 2) = V’/(V 1+V 2) Como V’~R 02 rint y V~R 03 Entonces H 12/(E 1+E 2) va a 0 con R 0 tendiendo a infinito rint
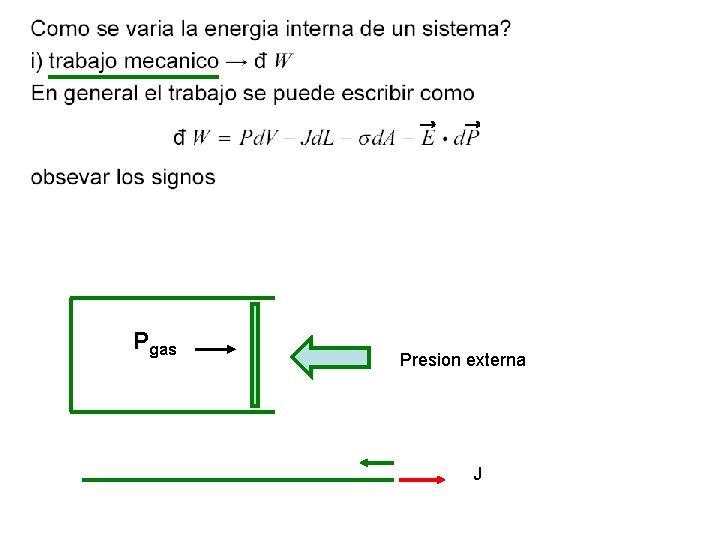
Pgas Presion externa J
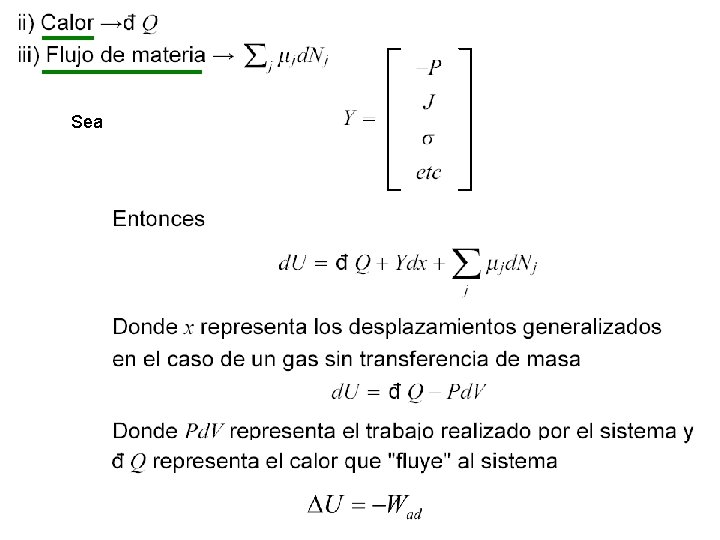
Sea

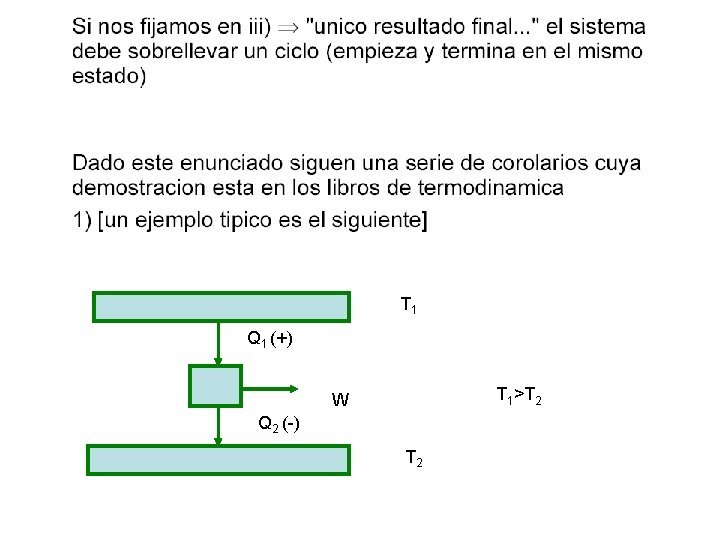
T 1 Q 1 (+) T 1>T 2 W Q 2 (-) T 2
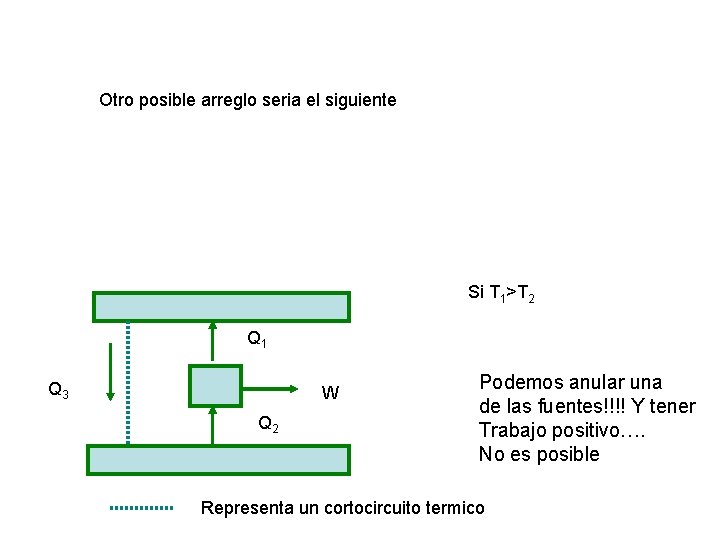
Otro posible arreglo seria el siguiente Si T 1>T 2 Q 1 Q 3 W Q 2 Podemos anular una de las fuentes!!!! Y tener Trabajo positivo…. No es posible Representa un cortocircuito termico

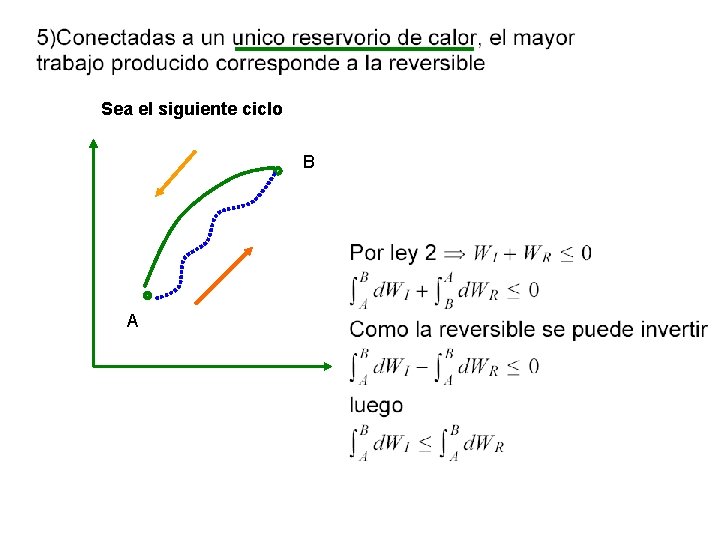
Sea el siguiente ciclo B A

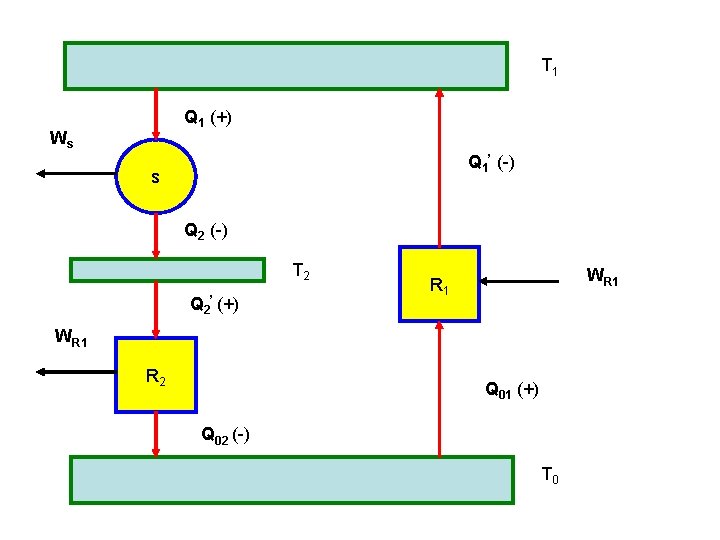
T 1 Q 1 (+) Ws Q 1’ (-) s Q 2 (-) T 2 Q 2’ (+) WR 1 R 2 Q 01 (+) Q 02 (-) T 0

T 1>T 2>T 0 (eliminamos T 2 y T 1) (queda unica fuente)


luego





Una definición precisa de equilibrio!

grado

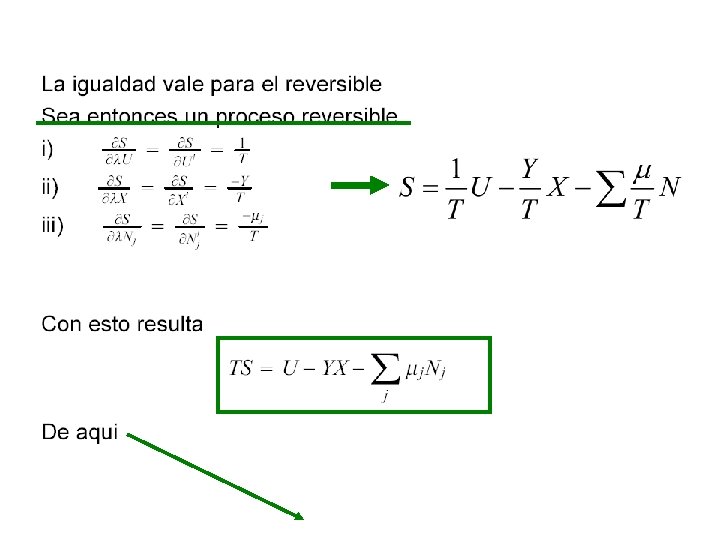
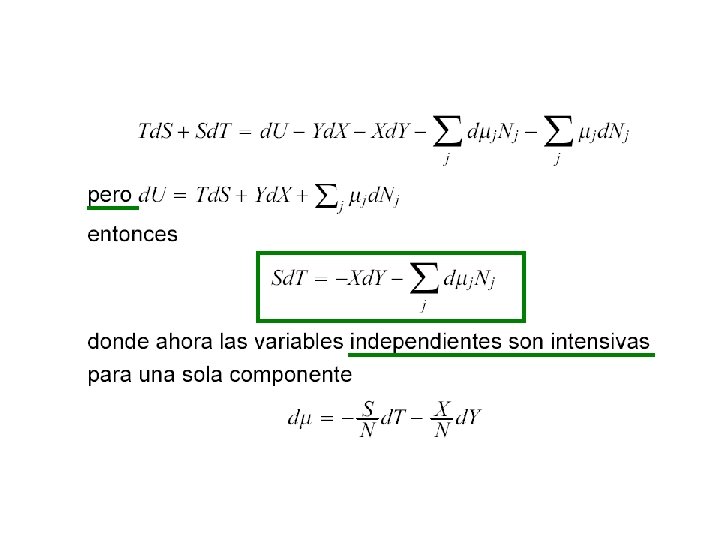


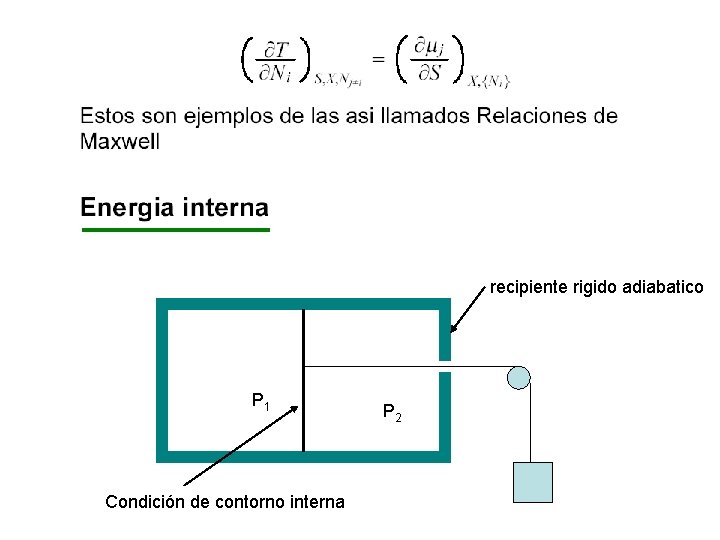
recipiente rigido adiabatico P 1 Condición de contorno interna P 2


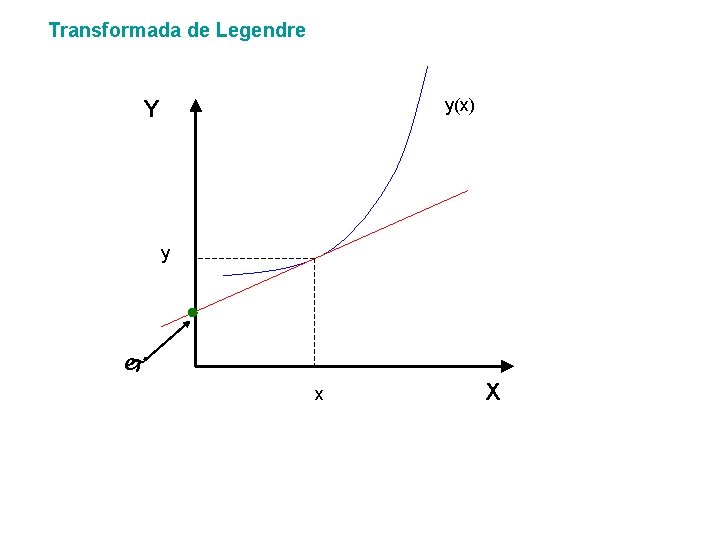
Transformada de Legendre y(x) Y y x X

Transformadas de Legendre


O tambien






- Slides: 59