Reconciling d 1 Masking in Hardware and Software

Reconciling d + 1 Masking in Hardware and Software Masked Hardware Hannes Gross , Stefan Mangard Graz University of Technology

In this work… • • Q: “Does randomness reduction pay off? ” 2

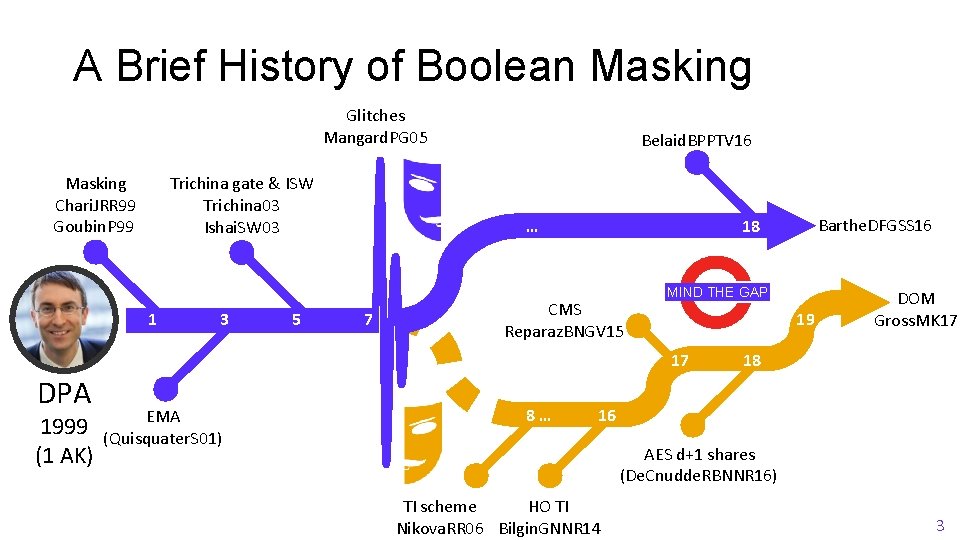
A Brief History of Boolean Masking Glitches Mangard. PG 05 Masking Chari. JRR 99 Goubin. P 99 Belaid. BPPTV 16 Trichina gate & ISW Trichina 03 Ishai. SW 03 1 3 5 … 7 9 CMS 11 13 Reparaz. BNGV 15 MIND THE GAP 15 17 DPA 1999 (1 AK) EMA (Quisquater. S 01) 8… Barthe. DFGSS 16 18 17 19 DOM Gross. MK 17 18 16 AES d+1 shares (De. Cnudde. RBNNR 16) TI scheme HO TI Nikova. RR 06 Bilgin. GNNR 14 3

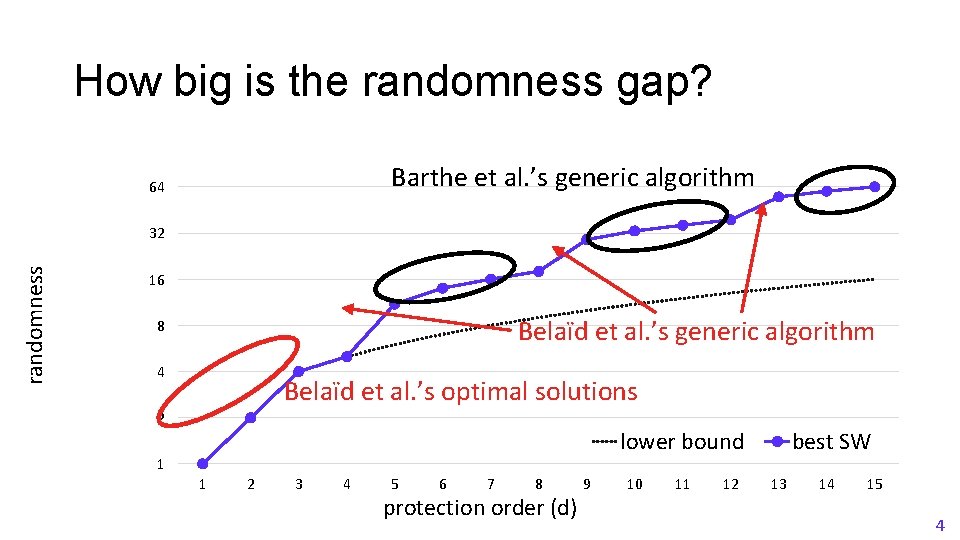
How big is the randomness gap? Barthe et al. ’s generic algorithm 64 randomness 32 16 Belaïd et al. ’s generic algorithm 8 4 Belaïd et al. ’s optimal solutions 2 lower bound 1 1 2 3 4 5 6 7 8 protection order (d) 9 10 11 12 best SW 13 14 15 4

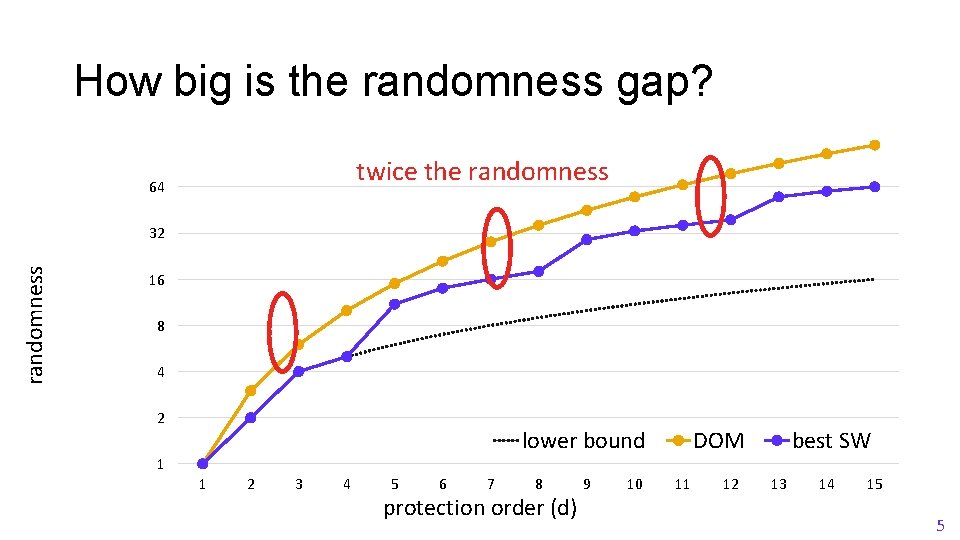
How big is the randomness gap? twice the randomness 64 randomness 32 16 8 4 2 lower bound 1 1 2 3 4 5 6 7 8 protection order (d) 9 10 DOM 11 12 best SW 13 14 15 5

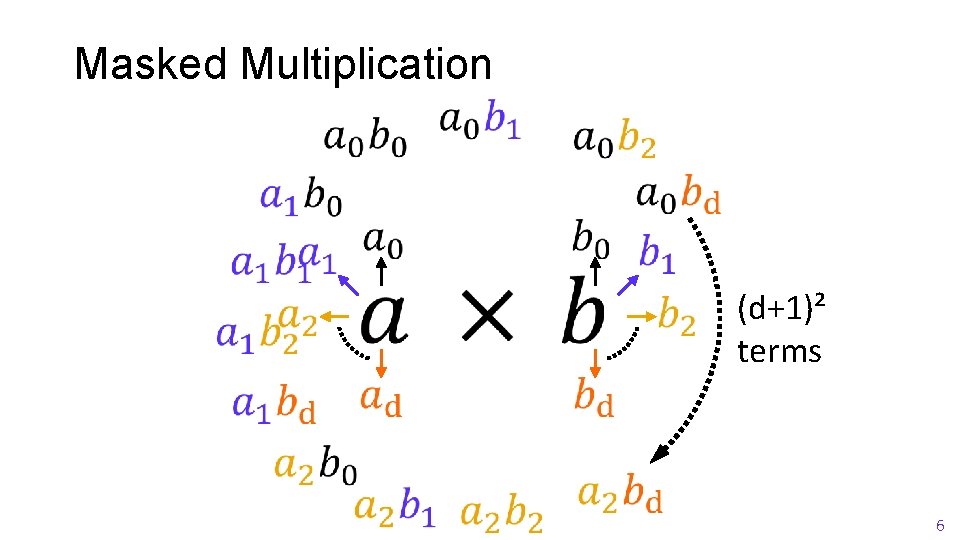
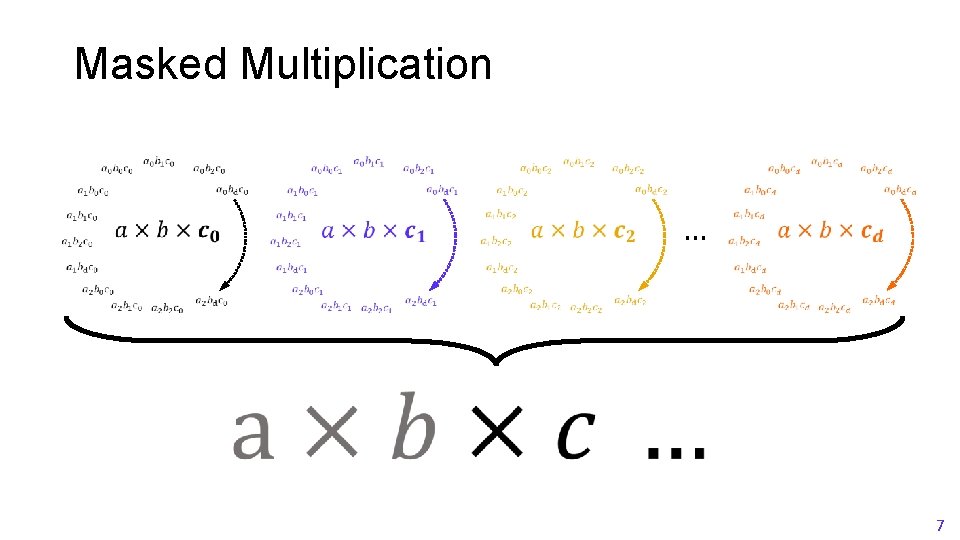
Masked Multiplication (d+1)² terms 6

Masked Multiplication … 7

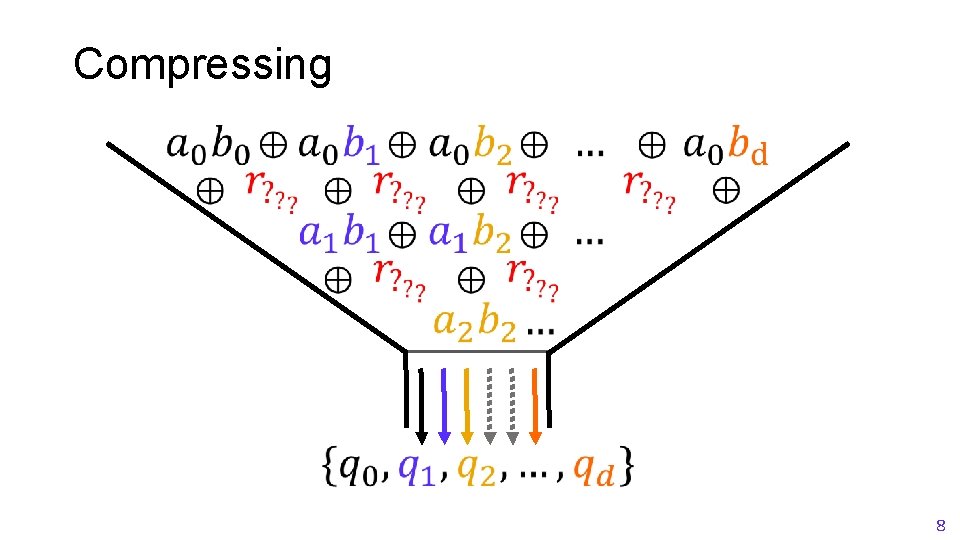
Compressing 8

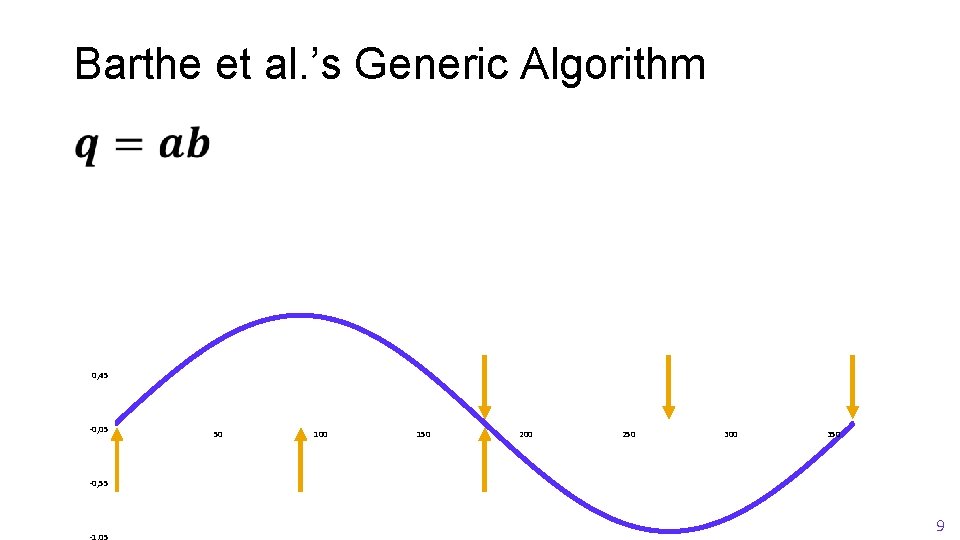
Barthe et al. ’s Generic Algorithm 0, 95 0, 45 -0, 05 0 50 100 150 200 250 300 350 -0, 55 -1, 05 9

10

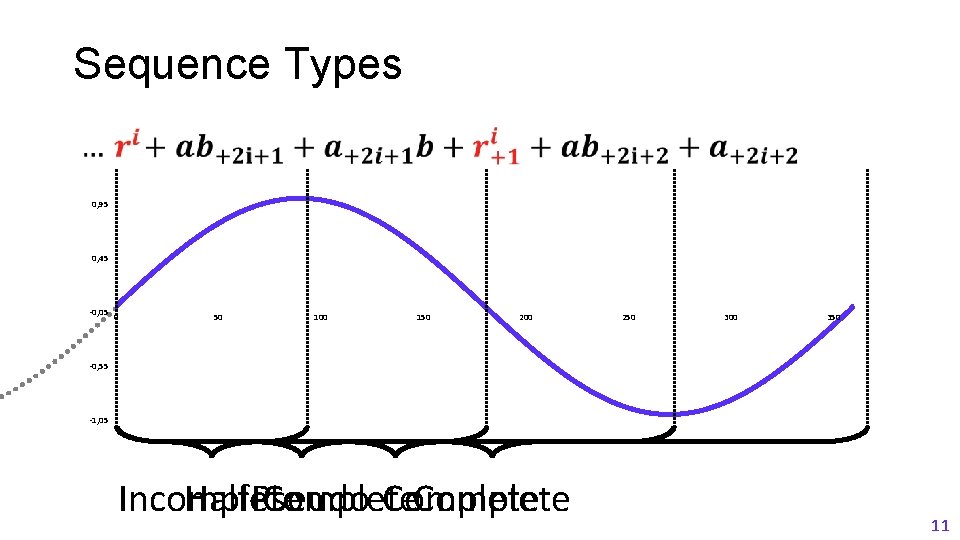
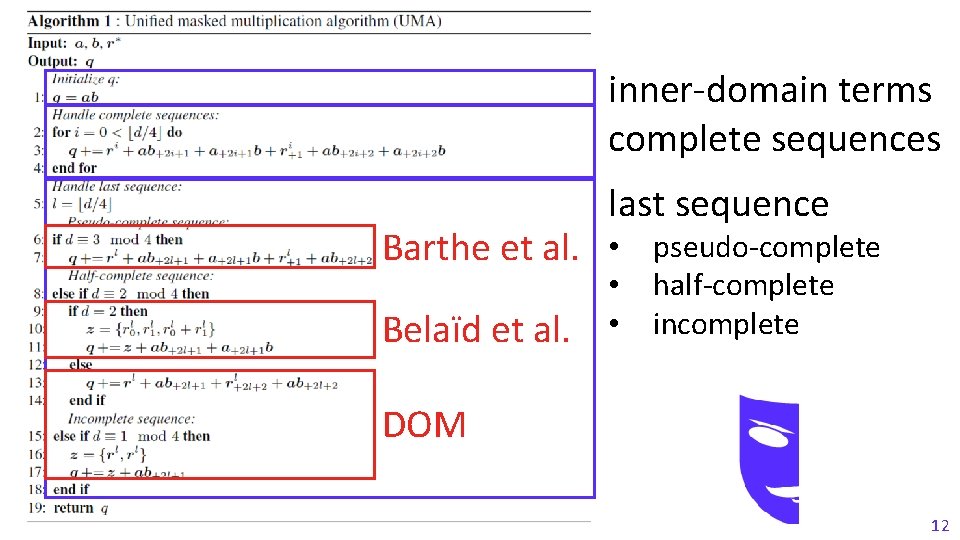
Sequence Types 0, 95 0, 45 -0, 05 0 50 100 150 200 250 300 350 -0, 55 -1, 05 Incomplete Half-Complete Pseudo-Complete 11

inner-domain terms complete sequences last sequence Barthe et al. • Belaïd et al. • • pseudo-complete half-complete incomplete DOM 12

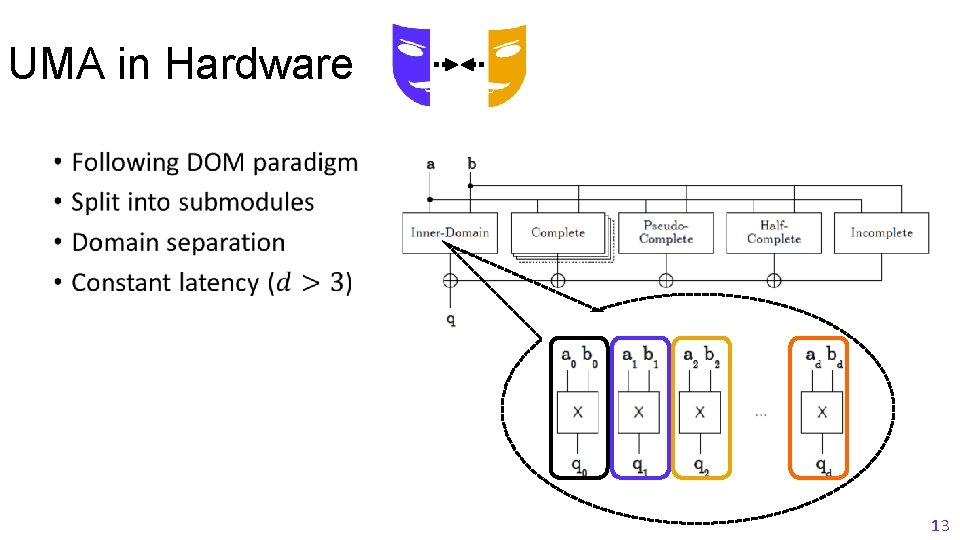
UMA in Hardware • 13

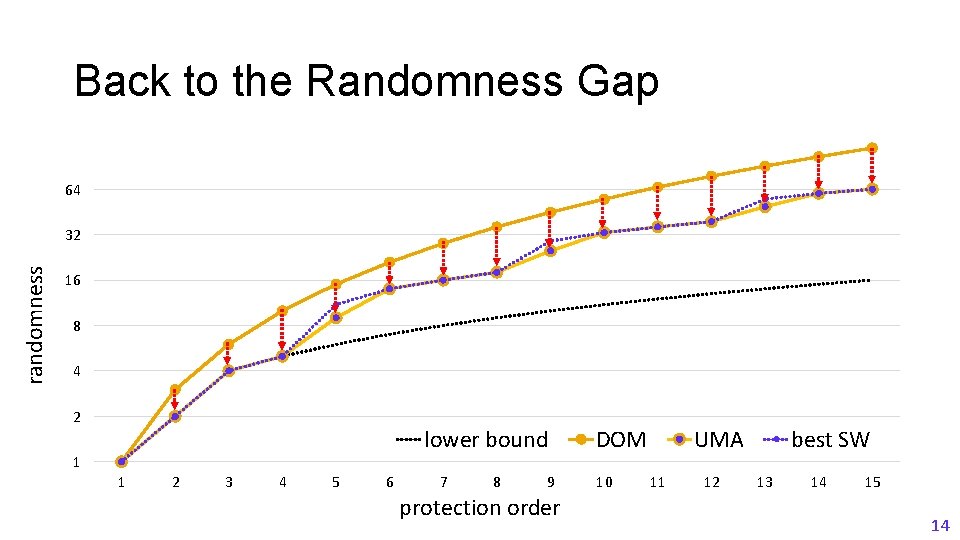
Back to the Randomness Gap 64 randomness 32 16 8 4 2 lower bound 1 1 2 3 4 5 6 7 8 9 protection order DOM 10 UMA 11 12 best SW 13 14 15 14

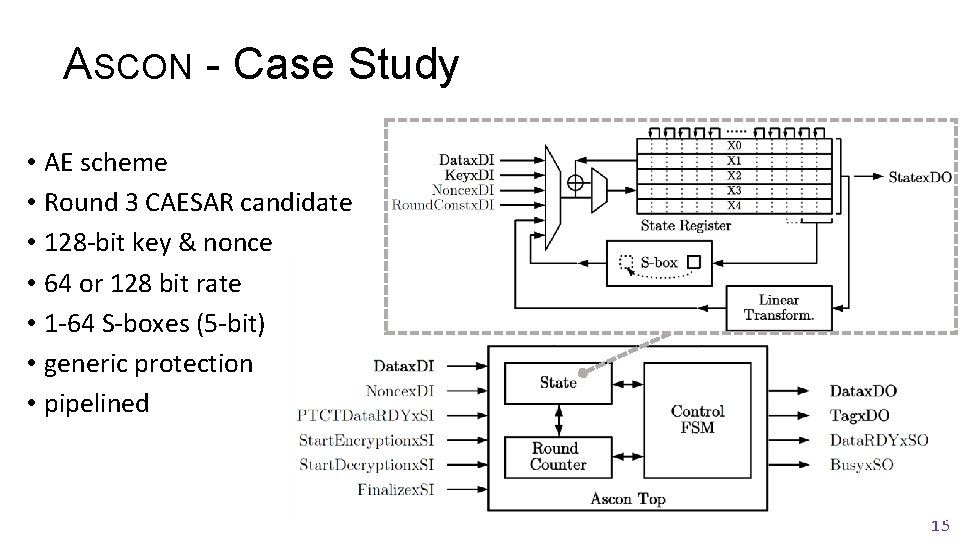
ASCON - Case Study • AE scheme • Round 3 CAESAR candidate • 128 -bit key & nonce • 64 or 128 bit rate • 1 -64 S-boxes (5 -bit) • generic protection • pipelined 15

Area: ASCON-Single Sbox [k. GE] UMA DOM 120 100 80 60 40 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 protection order 16

Area: ASCON-64 S-box [k. GE] UMA DOM 1 400 1 200 1 000 800 600 400 200 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 protection order 17

Throughput: ASCON-Single Sbox [Mb/s] UMA DOM 120 100 80 60 40 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 protection order 18

Throughput: ASCON-64 S-box [Mb/s] UMA DOM 2500 2000 1500 1000 500 Single S-box variants 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 protection order 19

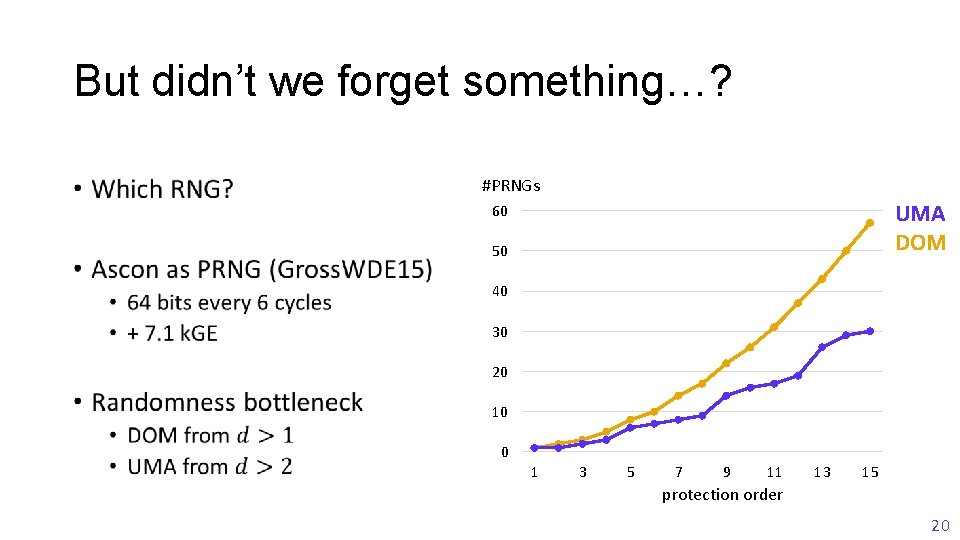
But didn’t we forget something…? • #PRNGs UMA DOM 60 50 40 30 20 10 0 1 3 5 7 9 11 13 15 protection order 20

Area with Randomness Costs [k. GE] UMA DOM 100 000, 00 10 000, 00 Single S-box variants 1 000, 00 10, 00 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 protection order 21

Conclusions Introduction of UMA • masking in SW and HW • ~d(d+1)/4 randomness UMA vs. DOM masked ASCON • • generic protection customizable (rate, S-Boxes, rounds, …) github. com/hgrosz including Ascon, AES, Keccak, RISC-V, … Randomness reduction does pay off • randomness = bottleneck • save randomness save area increase throughput 22

Reconciling d + 1 Masking in Hardware and Software Masked Hardware Hannes Gross , Stefan Mangard Graz University of Technology