Recommender Systems Collaborative Filtering Nonnegative Matrix Factorization Outlines

Recommender Systems • Collaborative Filtering • Non-negative Matrix Factorization

Outlines • What is a recommender system? • Several ways to build one: • Collaborative Filtering • Non-negative Matrix Factorization • …

Recommender Systems • It’s a platform/system/engine that seeks to predict the “rating” or “preference” a user would give to an item.

Applications (in real world) • Amazon. com recommends products based on purchase history.

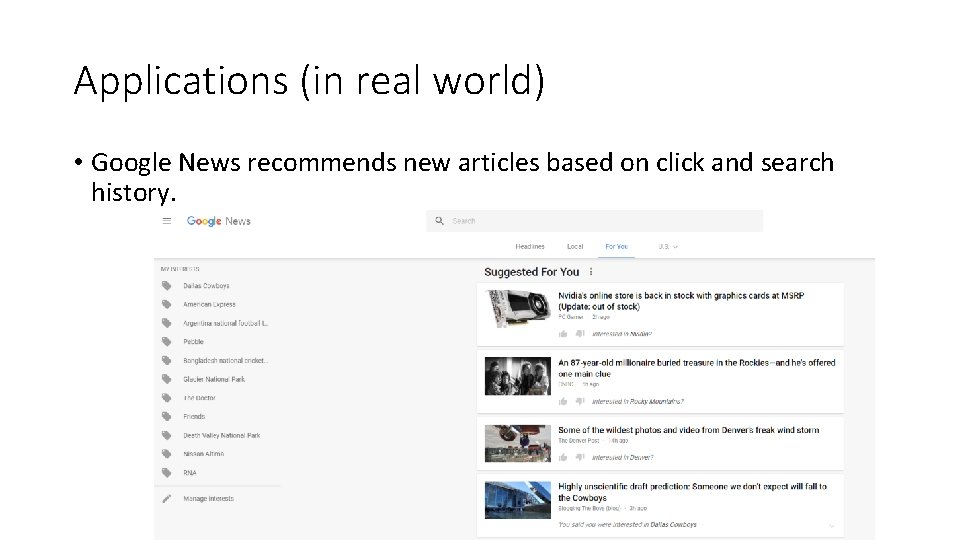
Applications (in real world) • Google News recommends new articles based on click and search history.

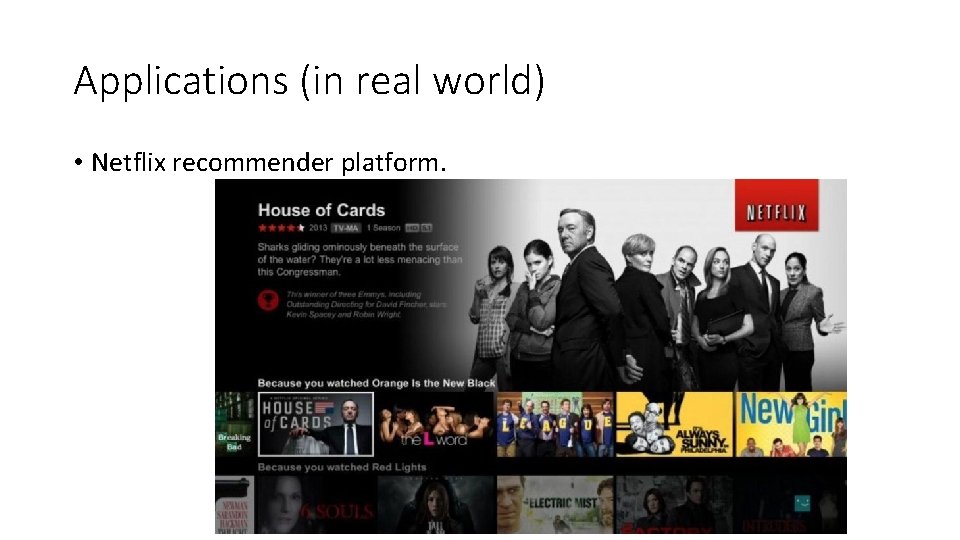
Applications (in real world) • Netflix recommender platform.

Netflix Prize •

What is Collaborative Filtering? • Intuition: Personal preferences are correlated. • If Alice loves items P and Q, and Bob loves P, Q and R, • Then Alice is more likely to love R • Collaborative Filtering Task • STEP 1: Discover patterns in observed preference behavior (e. g. , purchase history, item ratings, etc. ) across community of users. • STEP 2: Then predict new preferences based on those patterns. • It does not rely on item or user attributes (e. g. , demographic info, author, genre, producer, etc. )

What is collaborative Filtering?

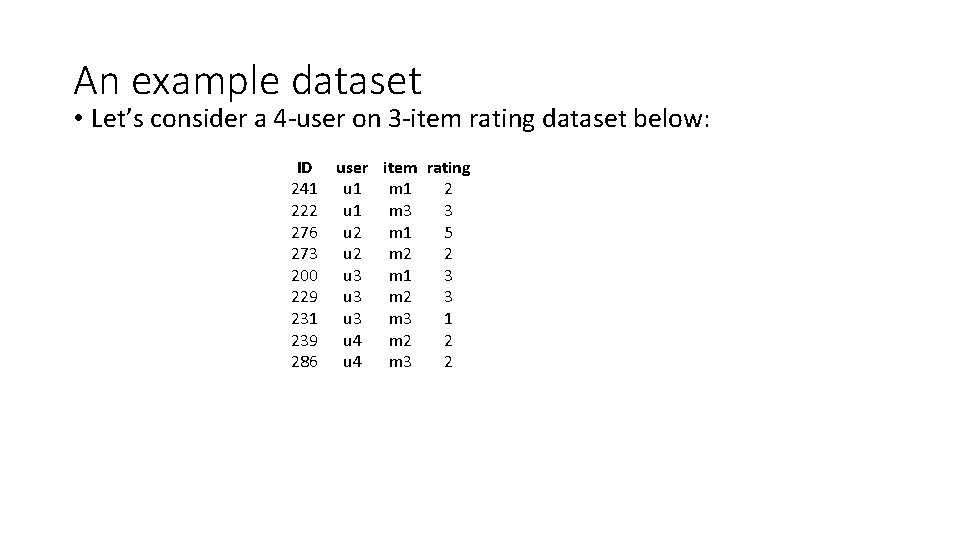
An example dataset • Let’s consider a 4 -user on 3 -item rating dataset below: ID 241 222 276 273 200 229 231 239 286 user item rating u 1 m 1 2 u 1 m 3 3 u 2 m 1 5 u 2 m 2 2 u 3 m 1 3 u 3 m 2 3 u 3 m 3 1 u 4 m 2 2 u 4 m 3 2

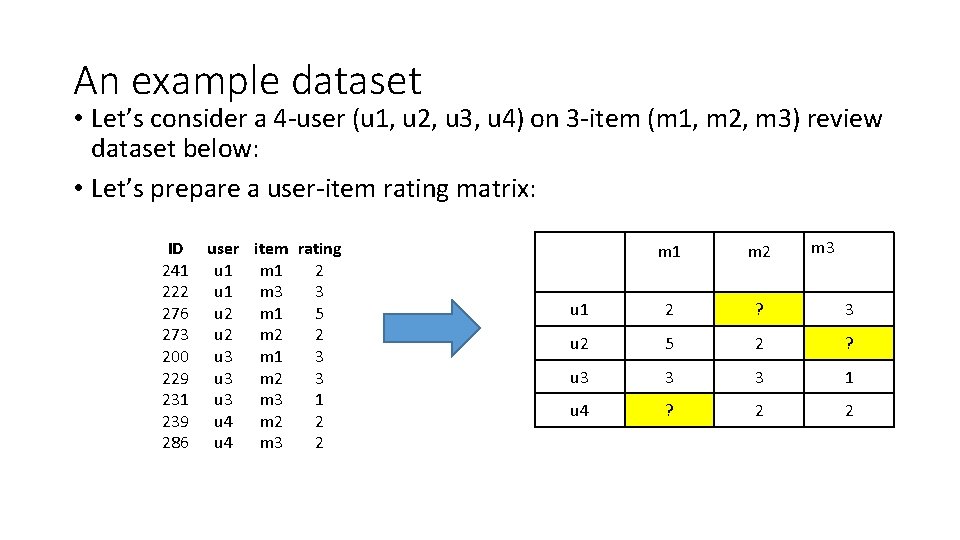
An example dataset • Let’s consider a 4 -user (u 1, u 2, u 3, u 4) on 3 -item (m 1, m 2, m 3) review dataset below: • Let’s prepare a user-item rating matrix: ID 241 222 276 273 200 229 231 239 286 user item rating u 1 m 1 2 u 1 m 3 3 u 2 m 1 5 u 2 m 2 2 u 3 m 1 3 u 3 m 2 3 u 3 m 3 1 u 4 m 2 2 u 4 m 3 2 m 3 m 1 m 2 u 1 2 ? 3 u 2 5 2 ? u 3 3 3 1 u 4 ? 2 2

What is collaborative Filtering?

(Item-based) Collaborative Filtering • The similarities between different items in the dataset are computed by using one from a number of similarity measures, then these similarity values are used to predict ratings for user-item pairs not present in the dataset. • Similarity measures: • Cosine similarity • Pearson correlation based similarity • Adjusted Cosine similarity

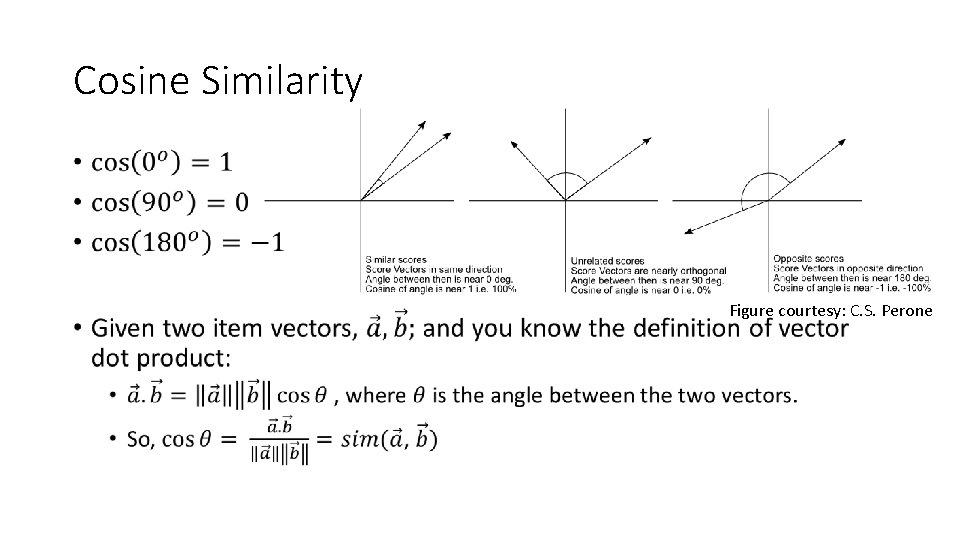
Cosine Similarity • Figure courtesy: C. S. Perone

User-item rating matrix Cosine Similarity • m 3 m 1 m 2 u 1 2 ? 3 u 2 5 2 ? u 3 3 3 1 u 4 ? 2 2

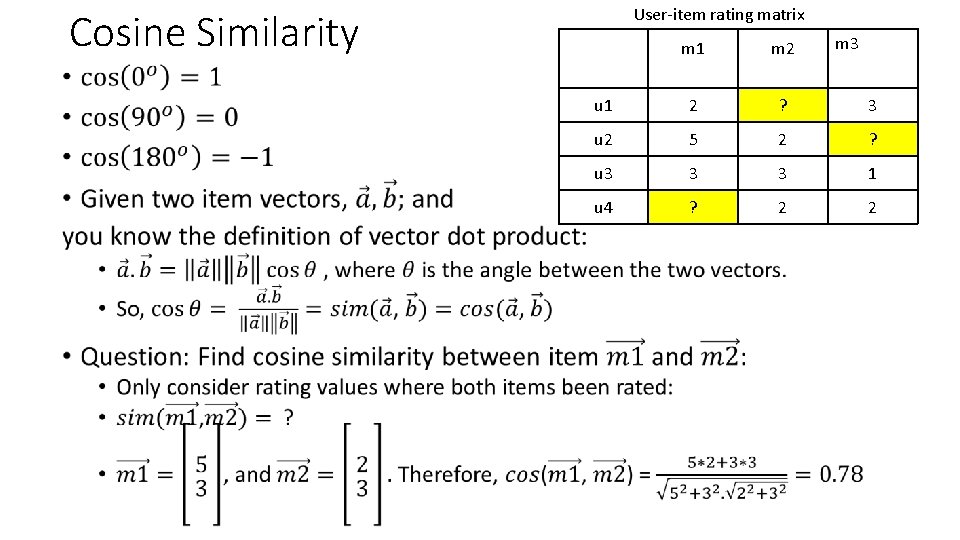
User-item rating matrix Cosine Similarity m 3 m 1 m 2 u 1 2 ? 3 u 2 5 2 ? u 3 3 3 1 u 4 ? 2 2 •

Complete the item-to-item similarity matrix m 1 m 2 m 3 m 1 Cos(m 1, m 1) Cos(m 1, m 2) Cos(m 1, m 3) m 2 Cos(m 2, m 1) Cos(m 2, m 2) Cos(m 2, m 3) m 3 Cos(m 3, m 1) Cos(m 3, m 2) Cos(m 3, m 3) • It’s a symmetric matrix. • Cos(x, x) = 1

Complete the item-to-item similarity matrix m 1 m 2 m 3 m 1 1 0. 76 0. 78 m 2 Cos(m 2, m 1) 1 0. 86 m 3 Cos(m 3, m 1) Cos(m 3, m 2) 1 • It’s a symmetric matrix. • Cos(x, x) = 1

Complete the item-to-item similarity matrix m 1 m 2 m 3 m 1 1 0. 76 0. 78 m 2 0. 76 1 0. 86 m 3 0. 78 0. 86 1 • It’s a symmetric matrix. • Cos(x, x) = 1

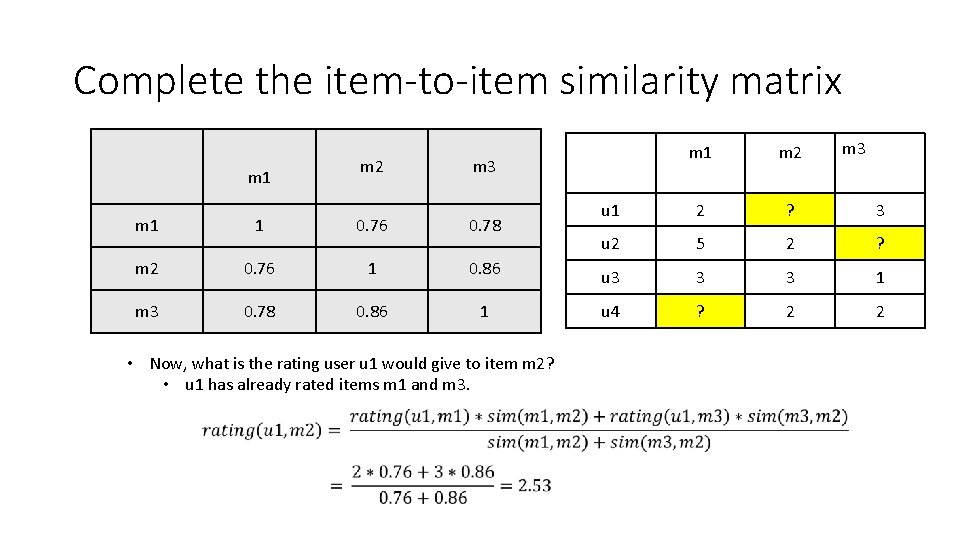
Complete the item-to-item similarity matrix m 2 m 1 1 0. 76 0. 78 m 2 0. 76 1 0. 86 m 3 0. 78 0. 86 1 • Now, what is the rating user u 1 would give to item m 2? • u 1 has already rated items m 1 and m 3. m 2 u 1 2 ? 3 u 2 5 2 ? u 3 3 3 1 u 4 ? 2 2 m 3 m 1

Non-negative Matrix Factorization (NMF) • Here a matrix V is factorized into two matrices W and H, • With the property that all three matrices have only non-negative elements. • The non-negativity property of elements makes the resulting matrices easier to inspect. • It can be solved by optimizing the following problem, and solve W and H: • Once solved, it can also be used as a recommender system. • Because V[i, j] = W[i, : ]*H[: , j]

How to solve NMF? • Let’s take a look at the whiteboard.

References • Item-based collaborative filtering recommendation algorithms, by Badrul et al. (WWW, 2001) • Algorithms for non-negative matrix factorization, by Lee and Seung (NIPS 2001) • A tutorial https: //lazyprogrammer. me/tutorial-on-collaborativefiltering-and-matrix-factorization-in-python/