Recommendations via Collaborative Filtering Recommendations Relevant for movies

Recommendations via Collaborative Filtering

Recommendations • Relevant for movies, restaurants, hotels…. • Recommendation Systems is a very hot topic in both academia and industry • The idea is to predict the opinion of users • Based on prior knowledge

The Netflix example • “For only $7. 99 a month, instantly watch unlimited movies & TV episodes streaming over the Internet to your TV via an Xbox 360, PS 3, Wii or any other device that streams from Netflix. You can also watch instantly on your computer too!”

? Where are the recommendations • One of the holy grails of Netflix is a sophisticated system that recommends movies to users • The “Net. Flix” challenge: – Improve the prediction of the system by 10% – Prize: 1 M dollars!

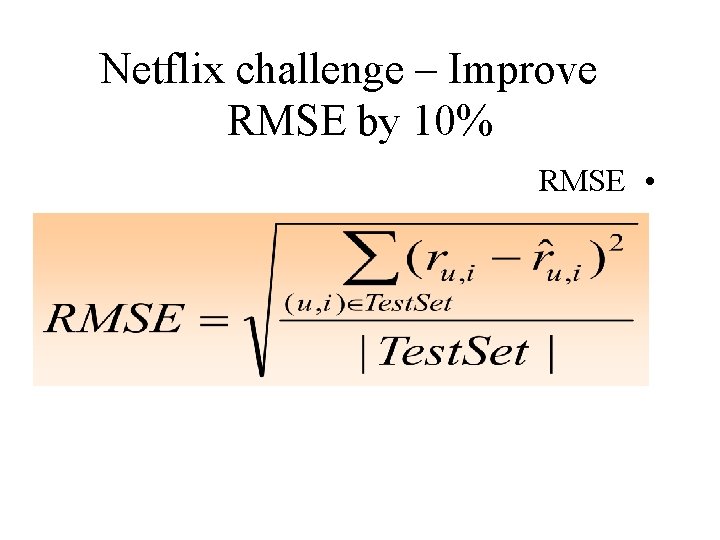
Netflix challenge – Improve RMSE by 10% RMSE •

Netflix Real-Life Data • ~20000 Movies • 2 M Users • Over 100 M Ratings • Large-scale…

Techniques • Many techniques, algorithms and heuristics • The winning algorithm used 107 (!!!!) different algorithmic approaches, blended into a single prediction • We will not talk about 107 approaches • We will overview some categories

Feature Extraction • Represent a movie as a binary vector of features • Genre, Language, Actors. . • The vector quickly gets pretty big • There are methods for compression

Looking for similar vectors • Intuition: if I like a movie, I may like movies with similar features • What about movies with similar features to the one with similar features? • Leads to Grouping movies by similarity of features • Also known as clustering

K-means • Randomly generate k centers • Assign each point to the nearest center, where "nearest" is defined with respect to a distance measure • Re-compute the new cluster centers. • Repeat the two previous steps until convergence of clusters

Another approach: Classification • The idea is to classify all movies = vectors to like don’t like • For a particular user • One popular technique is called Support Vector Machines

Linear SVM • Each point (=movie that the user saw) is mapped to 1 (like) or – 1 (don’t like) • We want to find a (hyper-)plane w*x –b=0 that minimizes the margin between w*x – b =1 (positive), w*x-b= -1 This becomes an optimization problem, good heuristics for solving it

Soft Margin SVM • Sometimes there is no hyperplane that can split the “like" and “unlike" cases • The Soft Margin method allows some slack for error • And still minimizes the distance to the correctly partitioned cases

Disadvantages • Vectors may be big • Accounts only for “local” preference of each user – Missing a lot of information from other users!

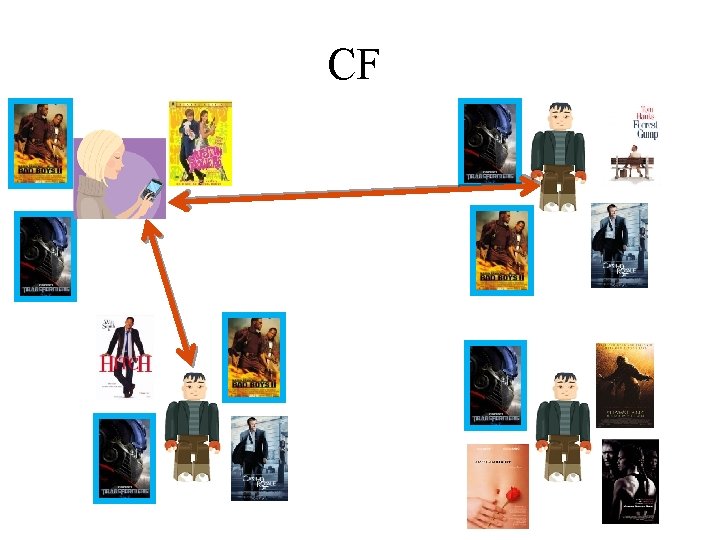
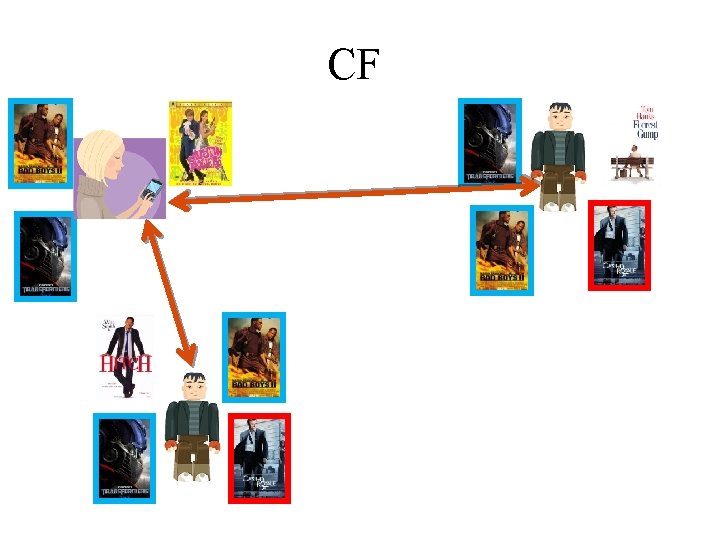
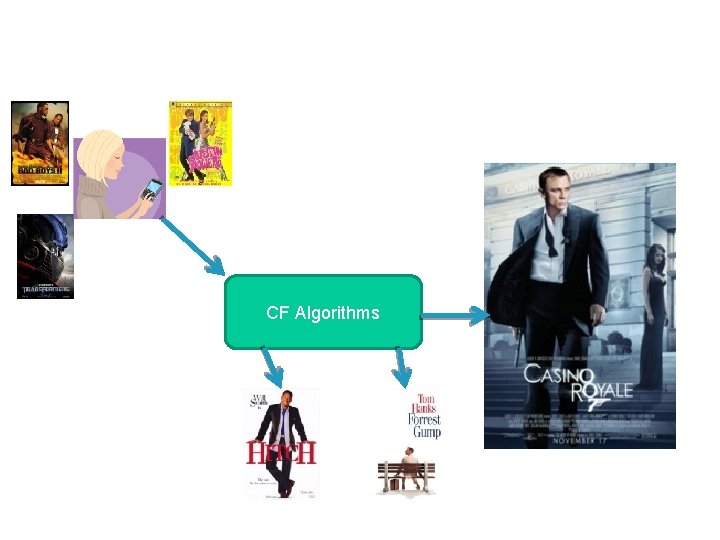
Collaborative Filtering • Use information gathered for other users, to infer something about the current user • Item-based CF: “Users who bought this book, also liked that book” – Can again use similarity between items (users that liked similar books…) • User-based CF is a bit more complicated

User Based Collaborative Filtering • Analyzes the relationships between users and items (movies) • Intuitively you will like movies that similar users like • Similar users are defined by those that like similar movies • Mutual recursion…

CF

CF

CF

CF

CF

CF Algorithms

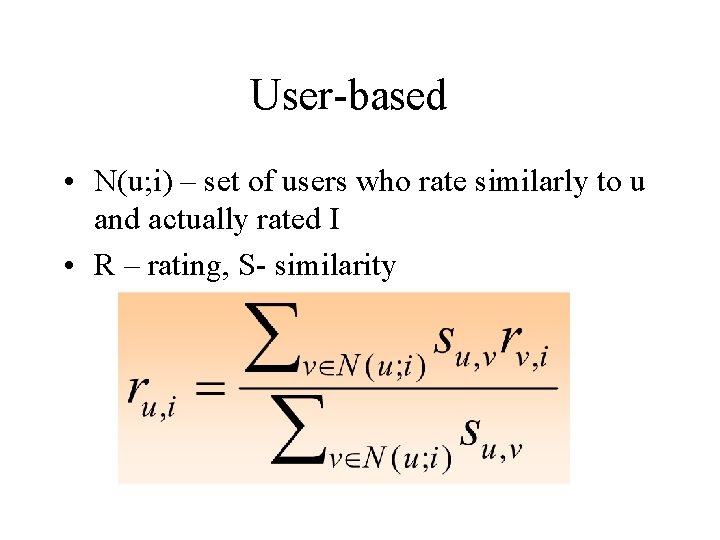
User-based • N(u; i) – set of users who rate similarly to u and actually rated I • R – rating, S- similarity

Su, v Key role! Used for: • Selecting N(u; i) • Weighting Most popular implementation • Pearson correlation coefficient

Pearson correlation coefficient • I(u, v) – Set of all items rated by both u and v

Can we do better? • We can use external information about the users • E. g. by Social networks • More ideas?

Privacy issues • Note that the methods we presented do not assume knowledge of the user real identities – Indeed in the Netflix challenge only masked identities were given • Still, to use in general some user profile should be built (even this may be a problem) – Avoided in the item-based approach • Using external information requires real identities. .